Abelemkpe, Jim Abeler, Jim Abeler

അബെലെംക്പെ: ഘാനയിലെ ഗ്രേറ്റർ അക്ര മേഖലയിലെ ഒരു ജില്ലയായ അക്ര മെട്രോപൊളിറ്റൻ ജില്ലയിലെ ഒരു നഗര പ്രദേശമാണ് അബെലെൻക്പെ .
ജിം അബെലർ: ജെയിംസ് ജെ. അബെലർ രണ്ടാമൻ ഒരു മിനസോട്ട രാഷ്ട്രീയക്കാരനും മിനസോട്ട സെനറ്റ് അംഗവുമാണ്. റിപ്പബ്ലിക്കൻ പാർട്ടി ഓഫ് മിനസോട്ടയിൽ അംഗമായ അദ്ദേഹം വടക്കൻ ഇരട്ട നഗരങ്ങളിലെ മെട്രോപൊളിറ്റൻ പ്രദേശത്തെ ജില്ലാ 35 പ്രതിനിധീകരിക്കുന്നു. അദ്ദേഹം മുമ്പ് മിനസോട്ട ജനപ്രതിനിധിസഭയിൽ ജില്ലാ 35 എയെ പ്രതിനിധീകരിച്ചു.
ജിം അബെലർ: ജെയിംസ് ജെ. അബെലർ രണ്ടാമൻ ഒരു മിനസോട്ട രാഷ്ട്രീയക്കാരനും മിനസോട്ട സെനറ്റ് അംഗവുമാണ്. റിപ്പബ്ലിക്കൻ പാർട്ടി ഓഫ് മിനസോട്ടയിൽ അംഗമായ അദ്ദേഹം വടക്കൻ ഇരട്ട നഗരങ്ങളിലെ മെട്രോപൊളിറ്റൻ പ്രദേശത്തെ ജില്ലാ 35 പ്രതിനിധീകരിക്കുന്നു. അദ്ദേഹം മുമ്പ് മിനസോട്ട ജനപ്രതിനിധിസഭയിൽ ജില്ലാ 35 എയെ പ്രതിനിധീകരിച്ചു.
അബെൽസ്: അബെലെസ് വേദപുസ്തക ആബേൽ കടപ്പെട്ടിരിക്കുന്നു ഒരു ഇംഗ്ലീഷ്, യഹൂദ മറു ആണ്. കുടുംബപ്പേരുള്ള ശ്രദ്ധേയരായ ആളുകൾ ഉൾപ്പെടുന്നു: ബെഞ്ചമിൻ അബെൽസ്, അമേരിക്കൻ ഭൗതികശാസ്ത്രജ്ഞൻ എഡ്വേർഡ് അബെൽസ് (1869-1919), അമേരിക്കൻ നടൻ ഫ്ലോറിൻ ആബെലസ് (1922-2005), ഫ്രഞ്ച് ഭൗതികശാസ്ത്രജ്ഞൻ ജോൺ എച്ച് അബെൽസ്, അമേരിക്കൻ വ്യവസായി കിം വിക്ടോറിയ അബെൽസ്, അമേരിക്കൻ ആർട്ടിസ്റ്റ് മിഷേൽ അബെൽസ്, അമേരിക്കൻ ആർട്ടിസ്റ്റ് പീറ്റർ അബെൽസ് (1924-1999), ഓസ്‌ട്രേലിയൻ വ്യവസായി മോഷെ അബെൽസ്, ഇസ്രായേലി മസ്തിഷ്ക ഗവേഷകൻ നോർമൻ അബെൽസ്, ഓസ്ട്രിയൻ വംശജനായ അമേരിക്കൻ സൈക്കോളജിസ്റ്റ് രൂത്ത് അബെൽസ്, ഇസ്രായേലി ഒളിമ്പിക് ജിംനാസ്റ്റ് സിഗ്മണ്ട് അബെൽസ്, അമേരിക്കൻ ഫിഗറേറ്റീവ് ആർട്ടിസ്റ്റ്
ബെഞ്ചമിൻ അബെൽസ്: ഓസ്ട്രിയൻ-ചെക്ക് ഭൗതികശാസ്ത്രജ്ഞനായിരുന്നു ബെഞ്ചമിൻ അബെൽസ് , 1960 കളിൽ യുഎസിൽ ജർമ്മനിയം-സിലിക്കൺ അലോയ്കളെക്കുറിച്ച് നടത്തിയ ഗവേഷണം വോയേജർ ബഹിരാകാശ പേടകങ്ങൾ പോലുള്ള ബഹിരാകാശ പേടകങ്ങളെ ശക്തിപ്പെടുത്തുന്നതിനുള്ള സാങ്കേതികവിദ്യയിലേക്ക് നയിച്ചു. ഓസ്ട്രിയയിലും ചെക്കോസ്ലോവാക്യയിലും വളർന്ന അദ്ദേഹം 1939 ൽ കിൻഡർട്രാൻസ്പോർട്ട് മിഷനുകളിലൊന്നിൽ യുകെയിലെത്തി. ചെക്കോസ്ലോവാക്യയിലെയും ഇസ്രായേലിലെയും യുദ്ധത്തിനുശേഷം ഭൗതികശാസ്ത്രത്തിൽ ഡോക്ടറേറ്റ് നേടി. യുഎസിൽ റിസർച്ച് ഫിസിസിസ്റ്റായി ജോലി ചെയ്യുകയും 1995 ൽ വിരമിക്കുകയും ചെയ്തു. 1979 ലെ സ്റ്റുവർട്ട് ബാലന്റൈൻ മെഡലും ന്യൂജേഴ്‌സി ഇൻവെന്റേഴ്‌സ് ഹാൾ ഓഫ് ഫെയിമിലേക്ക് (1991) അദ്ദേഹം പ്രവേശിച്ചതും ഉൾപ്പെടുന്നു.
പീറ്റർ അബെൽസ്: സർ പീറ്റർ എമിൽ ഹെർബർട്ട് അബെൽസ് , എസി ഒരു ഓസ്‌ട്രേലിയൻ ഗതാഗത മാഗ്നറ്റായിരുന്നു. ഹംഗറിയിൽ നിന്നുള്ള അഭയാർത്ഥിയായ അദ്ദേഹം ഓസ്ട്രേലിയയിൽ ഒരു ബിസിനസുകാരനായി. 1972 ൽ നൈറ്റ് ആയി.
ട്രാൻസ്ഫർ-മാട്രിക്സ് രീതി (ഒപ്റ്റിക്സ്): ഒരു തരംതിരിച്ച മാധ്യമത്തിലൂടെ വൈദ്യുതകാന്തിക അല്ലെങ്കിൽ ശബ്ദ തരംഗങ്ങളുടെ പ്രചരണം വിശകലനം ചെയ്യുന്നതിന് ഒപ്റ്റിക്സിലും ശബ്ദശാസ്ത്രത്തിലും ഉപയോഗിക്കുന്ന ഒരു രീതിയാണ് ട്രാൻസ്ഫർ-മാട്രിക്സ് രീതി . ആന്റി-റിഫ്ലെക്റ്റീവ് കോട്ടിംഗുകളുടെയും ഡീലക്‌ട്രിക് മിററുകളുടെയും രൂപകൽപ്പനയ്ക്ക് ഇത് ഉദാഹരണമാണ്.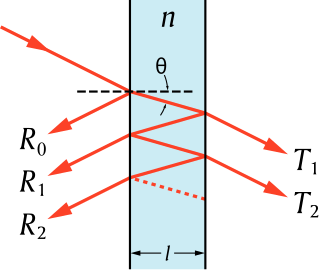
അബലെസ്സ: തെക്കൻ അൾജീരിയയിലെ തമൻറാസെറ്റ് പ്രവിശ്യയിലെ ഒരു പട്ടണവും കമ്മ്യൂണും ആണ് അബലെസ്സ , അതേ പേരിൽ ജില്ലയുമായി സഹകരിച്ച് പ്രവർത്തിക്കുന്നു. 2008 ലെ സെൻസസ് അനുസരിച്ച് 1998 ൽ 6,484 ൽ നിന്ന് 9,163 ജനസംഖ്യയുണ്ട്, വാർഷിക വളർച്ചാ നിരക്ക് 3.6%. പ്രവിശ്യയുടെ തലസ്ഥാനമായ തമൻറാസെറ്റ് നഗരത്തിന് 80 കിലോമീറ്റർ (50 മൈൽ) പടിഞ്ഞാറ് പുരാതന ട്രാൻസ്-സഹാറൻ വ്യാപാര പാതയിലാണ് അബലെസ്സ സ്ഥിതി ചെയ്യുന്നത്. 11120 ആണ് പട്ടണത്തിന്റെ പോസ്റ്റ് കോഡ്.
അബലെസ്സ: തെക്കൻ അൾജീരിയയിലെ തമൻറാസെറ്റ് പ്രവിശ്യയിലെ ഒരു പട്ടണവും കമ്മ്യൂണും ആണ് അബലെസ്സ , അതേ പേരിൽ ജില്ലയുമായി സഹകരിച്ച് പ്രവർത്തിക്കുന്നു. 2008 ലെ സെൻസസ് അനുസരിച്ച് 1998 ൽ 6,484 ൽ നിന്ന് 9,163 ജനസംഖ്യയുണ്ട്, വാർഷിക വളർച്ചാ നിരക്ക് 3.6%. പ്രവിശ്യയുടെ തലസ്ഥാനമായ തമൻറാസെറ്റ് നഗരത്തിന് 80 കിലോമീറ്റർ (50 മൈൽ) പടിഞ്ഞാറ് പുരാതന ട്രാൻസ്-സഹാറൻ വ്യാപാര പാതയിലാണ് അബലെസ്സ സ്ഥിതി ചെയ്യുന്നത്. 11120 ആണ് പട്ടണത്തിന്റെ പോസ്റ്റ് കോഡ്.
ജോഹാൻ ഫിലിപ്പ് അബെലിൻ: ജർമ്മൻ ചരിത്രകാരനായിരുന്നു ജോഹാൻ ഫിലിപ്പ് ആബെലിൻ , അദ്ദേഹത്തിന്റെ കരിയർ 16, 17 നൂറ്റാണ്ടുകളിൽ വ്യാപിച്ചു. 1634 നും 1637 നും ഇടയിൽ അദ്ദേഹം ജനിച്ചു. ഒരുപക്ഷേ, അബെലിയസ് , ഫിലിപ്പ് അർലാനിബ്യൂസ് , ജോഹാൻ ലുഡ്വിഗ് ഗോട്ട്ഫ്രൈഡ് , ഗോട്ടോഫ്രെഡസ് എന്നിവരുടെ ഓമനപ്പേരിൽ അദ്ദേഹം നിരവധി ചരിത്രങ്ങൾ എഴുതി.
ഓക്സിട്രിഗോണ ടാറ്റൈറ: അപിഡെ , ഗോത്ര മെലിപോനിനി എന്നീ കുടുംബങ്ങളിലെ യൂസോഷ്യൽ സ്റ്റിംഗ്‌ലെസ് തേനീച്ചയാണ് ഓക്സിട്രിഗോണ ടാറ്റൈറ , ടാറ്റാര അല്ലെങ്കിൽ അബെൽഹ-ഡി-ഫോഗോ എന്നറിയപ്പെടുന്നത്.
അബെൽഹലീം ഹസൻ അബ്ദുൽരാസിക് അഷ്കർ: പലസ്തീൻ മുസ്ലീം പ്രവർത്തകനാണ് അബെൽഹലീം ഹസൻ അബ്ദുൽരാസിക് അഷ്കർ , ചുരുക്കത്തിൽ, ഹോവാർഡ് സർവകലാശാലയിലെ ബിസിനസ് അസിസ്റ്റന്റ് പ്രൊഫസറായിരുന്നു. അമേരിക്കൻ ഐക്യനാടുകളിലെ ദാതാക്കളിൽ നിന്ന് ഹമാസിന് ധനസഹായം നൽകിയതുമായി ബന്ധപ്പെട്ട ഒരു വിചാരണയിൽ ഒരു മഹത്തായ ജൂറിക്ക് മുമ്പാകെ സാക്ഷ്യം വഹിക്കാൻ വിസമ്മതിച്ചതിന് നീതിയെ അവഹേളിച്ചതിനും തടസ്സപ്പെടുത്തിയതിനും ശിക്ഷിക്കപ്പെട്ടു. 2007 നവംബറിൽ 135 മാസം തടവിന് ശിക്ഷിക്കപ്പെട്ടു.
അബെൽഹലീം ഹസൻ അബ്ദുൽരാസിക് അഷ്കർ: പലസ്തീൻ മുസ്ലീം പ്രവർത്തകനാണ് അബെൽഹലീം ഹസൻ അബ്ദുൽരാസിക് അഷ്കർ , ചുരുക്കത്തിൽ, ഹോവാർഡ് സർവകലാശാലയിലെ ബിസിനസ് അസിസ്റ്റന്റ് പ്രൊഫസറായിരുന്നു. അമേരിക്കൻ ഐക്യനാടുകളിലെ ദാതാക്കളിൽ നിന്ന് ഹമാസിന് ധനസഹായം നൽകിയതുമായി ബന്ധപ്പെട്ട ഒരു വിചാരണയിൽ ഒരു മഹത്തായ ജൂറിക്ക് മുമ്പാകെ സാക്ഷ്യം വഹിക്കാൻ വിസമ്മതിച്ചതിന് നീതിയെ അവഹേളിച്ചതിനും തടസ്സപ്പെടുത്തിയതിനും ശിക്ഷിക്കപ്പെട്ടു. 2007 നവംബറിൽ 135 മാസം തടവിന് ശിക്ഷിക്കപ്പെട്ടു.
അബെൽഹൈറ: പോർച്ചുഗലിലെ ലോറിൻഹ മുനിസിപ്പാലിറ്റിയിലെ ഒരു ഗ്രാമമാണ് അബെൽഹീര .
Ābeļi പാരിഷ്: ലാത്വിയയിലെ ജകാബിൽസ് മുനിസിപ്പാലിറ്റിയുടെ അഡ്മിനിസ്ട്രേറ്റീവ് യൂണിറ്റാണ് ആബീ പാരിഷ് .
Ābeļi പാരിഷ്: ലാത്വിയയിലെ ജകാബിൽസ് മുനിസിപ്പാലിറ്റിയുടെ അഡ്മിനിസ്ട്രേറ്റീവ് യൂണിറ്റാണ് ആബീ പാരിഷ് .
അബെലിയ: മുപ്പതോളം ഇനങ്ങളും സങ്കരയിനങ്ങളും അടങ്ങിയ ഒരു അംഗീകൃത ജനുസ്സാണ് അബെലിയ , ഹണിസക്കിൾ കുടുംബമായ കാപ്രിഫോളിയേസിയിൽ. മോളിക്കുലാർ ഫ്യ്ലൊഗെനെതിച് പഠനങ്ങൾ ജനുസ്സാണ് മൊനൊഫ്യ്ലെതിച് അല്ല എന്ന്, 2013-ൽ, മേയാര്ടന് ഛ്രിസ്തെംഹുസ്ജ് അബെലിഅ ലയനം കയറി ലിന്നെഅ, മറ്റു ചില ഗെനെര സഹിതം മുന്നോട്ട് കാണിച്ചു. അബെലിഅ വിഭാഗം ജബെലിഅ ജനുസ്സാണ് ജബെലിഅ ഉയർത്തപ്പെട്ടു.
അബെലിയ (ഓർഗനൈസേഷൻ): നാഷണൽ കോൺഫെഡറേഷൻ ഓഫ് നോർവീജിയൻ എന്റർപ്രൈസസിന് കീഴിൽ സംഘടിപ്പിച്ച നോർവേയിലെ ഒരു തൊഴിലുടമയുടെ സംഘടനയാണ് അബെലിയ .
അബെലിയ (ഓർഗനൈസേഷൻ): നാഷണൽ കോൺഫെഡറേഷൻ ഓഫ് നോർവീജിയൻ എന്റർപ്രൈസസിന് കീഴിൽ സംഘടിപ്പിച്ച നോർവേയിലെ ഒരു തൊഴിലുടമയുടെ സംഘടനയാണ് അബെലിയ .
ലിന്നിയ ചിനെൻസിസ്: ഹണിസക്കിൾ കുടുംബത്തിലെ കാപ്രിഫോളിയേസിയിലെ പൂച്ചെടികളുടെ ഒരു ഇനമാണ് ലിന്നിയ ചിനെൻസിസ് , അബെലിയ ചിനെൻസിസ് , അബെലിയ റുപെസ്ട്രിസ്. ഇത് 1818 ൽ റോബർട്ട് ബ്ര rown ൺ വിവരിച്ചു , 1872 ൽ ലിന്നേയ ജനുസ്സിലേക്ക് മാറ്റി, ഈ നീക്കം 2013 വരെ വ്യാപകമായി അംഗീകരിക്കപ്പെട്ടിരുന്നില്ല. ചൈന, തായ്‌വാൻ, ജപ്പാൻ എന്നിവിടങ്ങളിൽ ഈ പ്ലാന്റ് വസിക്കുന്നു. ചുവന്ന കാണ്ഡം, തിളങ്ങുന്ന, ചെറിയ ഇലകൾ എന്നിവയുള്ള കോം‌പാക്റ്റ് ഇലപൊഴിക്കുന്ന കുറ്റിച്ചെടിയാണ് ശരത്കാലത്തിന് മുമ്പ് ചുവപ്പ് കലർന്ന തവിട്ട് നിറമാകുന്നത്. ജനുസ്സിലെ ഏറ്റവും തണുത്ത പ്രതിരോധശേഷിയുള്ള ഇനങ്ങളിൽ ഒന്നാണിത്.
ലിന്നിയ ചിനെൻസിസ്: ഹണിസക്കിൾ കുടുംബത്തിലെ കാപ്രിഫോളിയേസിയിലെ പൂച്ചെടികളുടെ ഒരു ഇനമാണ് ലിന്നിയ ചിനെൻസിസ് , അബെലിയ ചിനെൻസിസ് , അബെലിയ റുപെസ്ട്രിസ്. ഇത് 1818 ൽ റോബർട്ട് ബ്ര rown ൺ വിവരിച്ചു , 1872 ൽ ലിന്നേയ ജനുസ്സിലേക്ക് മാറ്റി, ഈ നീക്കം 2013 വരെ വ്യാപകമായി അംഗീകരിക്കപ്പെട്ടിരുന്നില്ല. ചൈന, തായ്‌വാൻ, ജപ്പാൻ എന്നിവിടങ്ങളിൽ ഈ പ്ലാന്റ് വസിക്കുന്നു. ചുവന്ന കാണ്ഡം, തിളങ്ങുന്ന, ചെറിയ ഇലകൾ എന്നിവയുള്ള കോം‌പാക്റ്റ് ഇലപൊഴിക്കുന്ന കുറ്റിച്ചെടിയാണ് ശരത്കാലത്തിന് മുമ്പ് ചുവപ്പ് കലർന്ന തവിട്ട് നിറമാകുന്നത്. ജനുസ്സിലെ ഏറ്റവും തണുത്ത പ്രതിരോധശേഷിയുള്ള ഇനങ്ങളിൽ ഒന്നാണിത്.
ലിന്നിയ ചിനെൻസിസ്: ഹണിസക്കിൾ കുടുംബത്തിലെ കാപ്രിഫോളിയേസിയിലെ പൂച്ചെടികളുടെ ഒരു ഇനമാണ് ലിന്നിയ ചിനെൻസിസ് , അബെലിയ ചിനെൻസിസ് , അബെലിയ റുപെസ്ട്രിസ്. ഇത് 1818 ൽ റോബർട്ട് ബ്ര rown ൺ വിവരിച്ചു , 1872 ൽ ലിന്നേയ ജനുസ്സിലേക്ക് മാറ്റി, ഈ നീക്കം 2013 വരെ വ്യാപകമായി അംഗീകരിക്കപ്പെട്ടിരുന്നില്ല. ചൈന, തായ്‌വാൻ, ജപ്പാൻ എന്നിവിടങ്ങളിൽ ഈ പ്ലാന്റ് വസിക്കുന്നു. ചുവന്ന കാണ്ഡം, തിളങ്ങുന്ന, ചെറിയ ഇലകൾ എന്നിവയുള്ള കോം‌പാക്റ്റ് ഇലപൊഴിക്കുന്ന കുറ്റിച്ചെടിയാണ് ശരത്കാലത്തിന് മുമ്പ് ചുവപ്പ് കലർന്ന തവിട്ട് നിറമാകുന്നത്. ജനുസ്സിലെ ഏറ്റവും തണുത്ത പ്രതിരോധശേഷിയുള്ള ഇനങ്ങളിൽ ഒന്നാണിത്.
അബെലിയ പള്ളി: പതിമൂന്നാം നൂറ്റാണ്ടിലെ ജോർജിയൻ ഓർത്തഡോക്സ് പള്ളിയാണ് ട്രിനിറ്റിയുടെ അബെലിയ ചർച്ച്, ജോർജിയയുടെ തെക്ക്-മധ്യമേഖലയായ ക്വെമോ കാർട്ട്‌ലിയിലെ ടെട്രി സ്ക്വാരോ മുനിസിപ്പാലിറ്റിയിൽ സ്ഥിതിചെയ്യുന്നു. ലളിതമായ സിംഗിൾ-നേവ് ഡിസൈൻ, ഇത് ഇന്നത്തെ അബെലിയാനി ഗ്രാമത്തിന്റെ പ്രാന്തപ്രദേശത്താണ് സ്ഥിതിചെയ്യുന്നത്. മംഗോളിയൻ ഭരണത്തിൻകീഴിൽ ജോർജിയയിലെ രാജഭരണത്തെക്കുറിച്ചുള്ള ഒരു പരാമർശം പള്ളിയുടെ തെക്കൻ മതിലിലെ ഒരു ലിഖിതത്തിൽ 1250–1259 കാലഘട്ടത്തിൽ നിർമ്മാണം ആരംഭിക്കുന്നത് സാധ്യമാക്കുന്നു. ജോർജിയയിലെ ദേശീയ പ്രാധാന്യത്തിന്റെ സ്ഥാവര സാംസ്കാരിക സ്മാരകങ്ങളുടെ പട്ടികയിൽ പള്ളി ആലേഖനം ചെയ്തിട്ടുണ്ട്.
സാബെലിയ കോറിംബോസ: ഹണിസക്കിൾ കുടുംബത്തിലെ കാപ്രിഫോളിയേസിയിലെ പൂച്ചെടികളുടെ ഒരു ഇനമാണ് സബീലിയ കോറിംബോസ . കസാക്കിസ്ഥാൻ, കിർഗിസ്ഥാൻ, താജിക്കിസ്ഥാൻ എന്നിവിടങ്ങളിൽ ഇത് സംഭവിക്കുന്നു.
ലിന്നിയ സ്പാതുലത: ഹണിസക്കിൾ കുടുംബത്തിലെ (കാപ്രിഫോളിയേസി) ലിന്നേയയുടെ ഒരു ഇനമാണ് ലിന്നിയ സ്പാത്തുലത , അബെലിയ സ്പാതുലത . ഈ പ്ലാന്റ് കൊറിയയ്ക്കും ജപ്പാനും ബാധകമാണ്.
ലിന്നിയ ഫ്ലോറിബുണ്ട: മെക്സിക്കോ സ്വദേശിയായ കാപ്രിഫോളിയേസി എന്ന ഹണിസക്കിൾ കുടുംബത്തിലെ പൂച്ചെടികളുടെ ഒരു ഇനമാണ് ലിന്നിയ ഫ്ലോറിബുണ്ട . 4 മീറ്റർ (13 അടി) ഉയരത്തിലും വീതിയിലും വളരുന്ന ഇത് 5 സെന്റിമീറ്റർ (2.0 ഇഞ്ച്) നീളമുള്ള തിളങ്ങുന്ന അണ്ഡാകാര ഇലകളും ട്യൂബുലാർ സെറൈസ് പുഷ്പങ്ങളുടെ കൂട്ടങ്ങളുമുള്ള അർദ്ധ നിത്യഹരിത അല്ലെങ്കിൽ നിത്യഹരിത കുറ്റിച്ചെടിയാണ്. −10 ° C (14 ° F) വരെ ഹാർഡി ആണെങ്കിലും ഇത് ഒരു അഭയസ്ഥാനമാണ് ഇഷ്ടപ്പെടുന്നത്, ഉദാഹരണത്തിന് തെക്ക് അഭിമുഖമായുള്ള കല്ല് മതിലിന് എതിരായി.
ലിന്നിയ × ഗ്രാൻഡിഫ്ലോറ: ലിന്നെഅ × ഗ്രാന്റിഫ്ളോറ, പര്യായ അബെലിഅ × ഗ്രാന്റിഫ്ളോറ, Honeysuckle കുടുംബം കാപ്രിഫോളിയേസി, എൽ ഉനിഫ്ലൊര കൂടെ എൽ ഛിനെംസിസ് ഹ്യ്ബ്രിദിസിന്ഗ് ഉന്നയിച്ച ചെടിയുടെ പൂവിടുമ്പോൾ ഒരു സങ്കരയിനത്തെ ആണ്.
ലിന്നിയ ചിനെൻസിസ്: ഹണിസക്കിൾ കുടുംബത്തിലെ കാപ്രിഫോളിയേസിയിലെ പൂച്ചെടികളുടെ ഒരു ഇനമാണ് ലിന്നിയ ചിനെൻസിസ് , അബെലിയ ചിനെൻസിസ് , അബെലിയ റുപെസ്ട്രിസ്. ഇത് 1818 ൽ റോബർട്ട് ബ്ര rown ൺ വിവരിച്ചു , 1872 ൽ ലിന്നേയ ജനുസ്സിലേക്ക് മാറ്റി, ഈ നീക്കം 2013 വരെ വ്യാപകമായി അംഗീകരിക്കപ്പെട്ടിരുന്നില്ല. ചൈന, തായ്‌വാൻ, ജപ്പാൻ എന്നിവിടങ്ങളിൽ ഈ പ്ലാന്റ് വസിക്കുന്നു. ചുവന്ന കാണ്ഡം, തിളങ്ങുന്ന, ചെറിയ ഇലകൾ എന്നിവയുള്ള കോം‌പാക്റ്റ് ഇലപൊഴിക്കുന്ന കുറ്റിച്ചെടിയാണ് ശരത്കാലത്തിന് മുമ്പ് ചുവപ്പ് കലർന്ന തവിട്ട് നിറമാകുന്നത്. ജനുസ്സിലെ ഏറ്റവും തണുത്ത പ്രതിരോധശേഷിയുള്ള ഇനങ്ങളിൽ ഒന്നാണിത്.
ലിന്നിയ ഫ്ലോറിബുണ്ട: മെക്സിക്കോ സ്വദേശിയായ കാപ്രിഫോളിയേസി എന്ന ഹണിസക്കിൾ കുടുംബത്തിലെ പൂച്ചെടികളുടെ ഒരു ഇനമാണ് ലിന്നിയ ഫ്ലോറിബുണ്ട . 4 മീറ്റർ (13 അടി) ഉയരത്തിലും വീതിയിലും വളരുന്ന ഇത് 5 സെന്റിമീറ്റർ (2.0 ഇഞ്ച്) നീളമുള്ള തിളങ്ങുന്ന അണ്ഡാകാര ഇലകളും ട്യൂബുലാർ സെറൈസ് പുഷ്പങ്ങളുടെ കൂട്ടങ്ങളുമുള്ള അർദ്ധ നിത്യഹരിത അല്ലെങ്കിൽ നിത്യഹരിത കുറ്റിച്ചെടിയാണ്. −10 ° C (14 ° F) വരെ ഹാർഡി ആണെങ്കിലും ഇത് ഒരു അഭയസ്ഥാനമാണ് ഇഷ്ടപ്പെടുന്നത്, ഉദാഹരണത്തിന് തെക്ക് അഭിമുഖമായുള്ള കല്ല് മതിലിന് എതിരായി.
ലിന്നിയ ചിനെൻസിസ്: ഹണിസക്കിൾ കുടുംബത്തിലെ കാപ്രിഫോളിയേസിയിലെ പൂച്ചെടികളുടെ ഒരു ഇനമാണ് ലിന്നിയ ചിനെൻസിസ് , അബെലിയ ചിനെൻസിസ് , അബെലിയ റുപെസ്ട്രിസ്. ഇത് 1818 ൽ റോബർട്ട് ബ്ര rown ൺ വിവരിച്ചു , 1872 ൽ ലിന്നേയ ജനുസ്സിലേക്ക് മാറ്റി, ഈ നീക്കം 2013 വരെ വ്യാപകമായി അംഗീകരിക്കപ്പെട്ടിരുന്നില്ല. ചൈന, തായ്‌വാൻ, ജപ്പാൻ എന്നിവിടങ്ങളിൽ ഈ പ്ലാന്റ് വസിക്കുന്നു. ചുവന്ന കാണ്ഡം, തിളങ്ങുന്ന, ചെറിയ ഇലകൾ എന്നിവയുള്ള കോം‌പാക്റ്റ് ഇലപൊഴിക്കുന്ന കുറ്റിച്ചെടിയാണ് ശരത്കാലത്തിന് മുമ്പ് ചുവപ്പ് കലർന്ന തവിട്ട് നിറമാകുന്നത്. ജനുസ്സിലെ ഏറ്റവും തണുത്ത പ്രതിരോധശേഷിയുള്ള ഇനങ്ങളിൽ ഒന്നാണിത്.
ലിന്നിയ സ്പാതുലത: ഹണിസക്കിൾ കുടുംബത്തിലെ (കാപ്രിഫോളിയേസി) ലിന്നേയയുടെ ഒരു ഇനമാണ് ലിന്നിയ സ്പാത്തുലത , അബെലിയ സ്പാതുലത . ഈ പ്ലാന്റ് കൊറിയയ്ക്കും ജപ്പാനും ബാധകമാണ്.
ലിന്നിയ ചിനെൻസിസ്: ഹണിസക്കിൾ കുടുംബത്തിലെ കാപ്രിഫോളിയേസിയിലെ പൂച്ചെടികളുടെ ഒരു ഇനമാണ് ലിന്നിയ ചിനെൻസിസ് , അബെലിയ ചിനെൻസിസ് , അബെലിയ റുപെസ്ട്രിസ്. ഇത് 1818 ൽ റോബർട്ട് ബ്ര rown ൺ വിവരിച്ചു , 1872 ൽ ലിന്നേയ ജനുസ്സിലേക്ക് മാറ്റി, ഈ നീക്കം 2013 വരെ വ്യാപകമായി അംഗീകരിക്കപ്പെട്ടിരുന്നില്ല. ചൈന, തായ്‌വാൻ, ജപ്പാൻ എന്നിവിടങ്ങളിൽ ഈ പ്ലാന്റ് വസിക്കുന്നു. ചുവന്ന കാണ്ഡം, തിളങ്ങുന്ന, ചെറിയ ഇലകൾ എന്നിവയുള്ള കോം‌പാക്റ്റ് ഇലപൊഴിക്കുന്ന കുറ്റിച്ചെടിയാണ് ശരത്കാലത്തിന് മുമ്പ് ചുവപ്പ് കലർന്ന തവിട്ട് നിറമാകുന്നത്. ജനുസ്സിലെ ഏറ്റവും തണുത്ത പ്രതിരോധശേഷിയുള്ള ഇനങ്ങളിൽ ഒന്നാണിത്.
ലിന്നിയ പാർവിഫോളിയ: മധ്യ ചൈന സ്വദേശിയായ കാപ്രിഫോളിയേസി കുടുംബത്തിലെ പൂച്ചെടികളുടെ ഒരു ഇനമാണ് ലിന്നിയ പാർവിഫോളിയ , അബെലിയ ഷുമാന്നി . 2 മീറ്റർ (7 അടി) ഉയരത്തിൽ 3 മീറ്റർ (10 അടി) വീതിയിൽ വളരുന്ന അർദ്ധ നിത്യഹരിത കുറ്റിച്ചെടിയാണിത്. ചുവന്ന കാലിസുള്ള പിങ്ക് പൂക്കൾ വേനൽക്കാലത്തിന്റെ അവസാനത്തിലും ശരത്കാലത്തും ഉത്പാദിപ്പിക്കപ്പെടുന്നു.
ലിന്നിയ പാർവിഫോളിയ: മധ്യ ചൈന സ്വദേശിയായ കാപ്രിഫോളിയേസി കുടുംബത്തിലെ പൂച്ചെടികളുടെ ഒരു ഇനമാണ് ലിന്നിയ പാർവിഫോളിയ , അബെലിയ ഷുമാന്നി . 2 മീറ്റർ (7 അടി) ഉയരത്തിൽ 3 മീറ്റർ (10 അടി) വീതിയിൽ വളരുന്ന അർദ്ധ നിത്യഹരിത കുറ്റിച്ചെടിയാണിത്. ചുവന്ന കാലിസുള്ള പിങ്ക് പൂക്കൾ വേനൽക്കാലത്തിന്റെ അവസാനത്തിലും ശരത്കാലത്തും ഉത്പാദിപ്പിക്കപ്പെടുന്നു.
സാബെലിയ ത്യാഹിയോണി: സുഗന്ധമുള്ള അബെലിയ എന്നറിയപ്പെടുന്ന അബെലിയ മൊസാനെൻസിസ് എന്ന പര്യായമായ സബേലിയ ടിയാഹിയോണി , ഹണിസക്കിൾ കുടുംബത്തിലെ കാപ്രിഫോളിയേസിയിലെ ഇലപൊഴിക്കുന്ന കുറ്റിച്ചെടിയാണ്. 2 മീറ്റർ ഉയരത്തിലും വീതിയിലും വളരുന്ന ഇത് പല അനുബന്ധ ഇനങ്ങളേക്കാളും കഠിനമാണ്, താപനില −20 ° C (−4 ° F) വരെ കുറവാണ്. ട്യൂബുലാർ പൂക്കൾ പിങ്ക് കലർന്ന വെളുത്തതും വളരെ സുഗന്ധമുള്ളതുമാണ്, വസന്തത്തിന്റെ അവസാനത്തിൽ പ്രത്യക്ഷപ്പെടുന്നു. തിളങ്ങുന്ന പച്ച ഇലകൾ വീഴുന്നതിന് മുമ്പ് ശരത്കാലത്തിലാണ് ചുവപ്പായി മാറുന്നത്.
ലിന്നിയ പാർവിഫോളിയ: മധ്യ ചൈന സ്വദേശിയായ കാപ്രിഫോളിയേസി കുടുംബത്തിലെ പൂച്ചെടികളുടെ ഒരു ഇനമാണ് ലിന്നിയ പാർവിഫോളിയ , അബെലിയ ഷുമാന്നി . 2 മീറ്റർ (7 അടി) ഉയരത്തിൽ 3 മീറ്റർ (10 അടി) വീതിയിൽ വളരുന്ന അർദ്ധ നിത്യഹരിത കുറ്റിച്ചെടിയാണിത്. ചുവന്ന കാലിസുള്ള പിങ്ക് പൂക്കൾ വേനൽക്കാലത്തിന്റെ അവസാനത്തിലും ശരത്കാലത്തും ഉത്പാദിപ്പിക്കപ്പെടുന്നു.
ലിന്നിയ പാർവിഫോളിയ: മധ്യ ചൈന സ്വദേശിയായ കാപ്രിഫോളിയേസി കുടുംബത്തിലെ പൂച്ചെടികളുടെ ഒരു ഇനമാണ് ലിന്നിയ പാർവിഫോളിയ , അബെലിയ ഷുമാന്നി . 2 മീറ്റർ (7 അടി) ഉയരത്തിൽ 3 മീറ്റർ (10 അടി) വീതിയിൽ വളരുന്ന അർദ്ധ നിത്യഹരിത കുറ്റിച്ചെടിയാണിത്. ചുവന്ന കാലിസുള്ള പിങ്ക് പൂക്കൾ വേനൽക്കാലത്തിന്റെ അവസാനത്തിലും ശരത്കാലത്തും ഉത്പാദിപ്പിക്കപ്പെടുന്നു.
ലിന്നിയ ചിനെൻസിസ്: ഹണിസക്കിൾ കുടുംബത്തിലെ കാപ്രിഫോളിയേസിയിലെ പൂച്ചെടികളുടെ ഒരു ഇനമാണ് ലിന്നിയ ചിനെൻസിസ് , അബെലിയ ചിനെൻസിസ് , അബെലിയ റുപെസ്ട്രിസ്. ഇത് 1818 ൽ റോബർട്ട് ബ്ര rown ൺ വിവരിച്ചു , 1872 ൽ ലിന്നേയ ജനുസ്സിലേക്ക് മാറ്റി, ഈ നീക്കം 2013 വരെ വ്യാപകമായി അംഗീകരിക്കപ്പെട്ടിരുന്നില്ല. ചൈന, തായ്‌വാൻ, ജപ്പാൻ എന്നിവിടങ്ങളിൽ ഈ പ്ലാന്റ് വസിക്കുന്നു. ചുവന്ന കാണ്ഡം, തിളങ്ങുന്ന, ചെറിയ ഇലകൾ എന്നിവയുള്ള കോം‌പാക്റ്റ് ഇലപൊഴിക്കുന്ന കുറ്റിച്ചെടിയാണ് ശരത്കാലത്തിന് മുമ്പ് ചുവപ്പ് കലർന്ന തവിട്ട് നിറമാകുന്നത്. ജനുസ്സിലെ ഏറ്റവും തണുത്ത പ്രതിരോധശേഷിയുള്ള ഇനങ്ങളിൽ ഒന്നാണിത്.
ലിന്നിയ സ്പാതുലത: ഹണിസക്കിൾ കുടുംബത്തിലെ (കാപ്രിഫോളിയേസി) ലിന്നേയയുടെ ഒരു ഇനമാണ് ലിന്നിയ സ്പാത്തുലത , അബെലിയ സ്പാതുലത . ഈ പ്ലാന്റ് കൊറിയയ്ക്കും ജപ്പാനും ബാധകമാണ്.
ലിന്നിയ പാർവിഫോളിയ: മധ്യ ചൈന സ്വദേശിയായ കാപ്രിഫോളിയേസി കുടുംബത്തിലെ പൂച്ചെടികളുടെ ഒരു ഇനമാണ് ലിന്നിയ പാർവിഫോളിയ , അബെലിയ ഷുമാന്നി . 2 മീറ്റർ (7 അടി) ഉയരത്തിൽ 3 മീറ്റർ (10 അടി) വീതിയിൽ വളരുന്ന അർദ്ധ നിത്യഹരിത കുറ്റിച്ചെടിയാണിത്. ചുവന്ന കാലിസുള്ള പിങ്ക് പൂക്കൾ വേനൽക്കാലത്തിന്റെ അവസാനത്തിലും ശരത്കാലത്തും ഉത്പാദിപ്പിക്കപ്പെടുന്നു.
ലിന്നിയ പാർവിഫോളിയ: മധ്യ ചൈന സ്വദേശിയായ കാപ്രിഫോളിയേസി കുടുംബത്തിലെ പൂച്ചെടികളുടെ ഒരു ഇനമാണ് ലിന്നിയ പാർവിഫോളിയ , അബെലിയ ഷുമാന്നി . 2 മീറ്റർ (7 അടി) ഉയരത്തിൽ 3 മീറ്റർ (10 അടി) വീതിയിൽ വളരുന്ന അർദ്ധ നിത്യഹരിത കുറ്റിച്ചെടിയാണിത്. ചുവന്ന കാലിസുള്ള പിങ്ക് പൂക്കൾ വേനൽക്കാലത്തിന്റെ അവസാനത്തിലും ശരത്കാലത്തും ഉത്പാദിപ്പിക്കപ്പെടുന്നു.
ലിന്നിയ സ്പാതുലത: ഹണിസക്കിൾ കുടുംബത്തിലെ (കാപ്രിഫോളിയേസി) ലിന്നേയയുടെ ഒരു ഇനമാണ് ലിന്നിയ സ്പാത്തുലത , അബെലിയ സ്പാതുലത . ഈ പ്ലാന്റ് കൊറിയയ്ക്കും ജപ്പാനും ബാധകമാണ്.
ലിന്നിയ ഫ്ലോറിബുണ്ട: മെക്സിക്കോ സ്വദേശിയായ കാപ്രിഫോളിയേസി എന്ന ഹണിസക്കിൾ കുടുംബത്തിലെ പൂച്ചെടികളുടെ ഒരു ഇനമാണ് ലിന്നിയ ഫ്ലോറിബുണ്ട . 4 മീറ്റർ (13 അടി) ഉയരത്തിലും വീതിയിലും വളരുന്ന ഇത് 5 സെന്റിമീറ്റർ (2.0 ഇഞ്ച്) നീളമുള്ള തിളങ്ങുന്ന അണ്ഡാകാര ഇലകളും ട്യൂബുലാർ സെറൈസ് പുഷ്പങ്ങളുടെ കൂട്ടങ്ങളുമുള്ള അർദ്ധ നിത്യഹരിത അല്ലെങ്കിൽ നിത്യഹരിത കുറ്റിച്ചെടിയാണ്. −10 ° C (14 ° F) വരെ ഹാർഡി ആണെങ്കിലും ഇത് ഒരു അഭയസ്ഥാനമാണ് ഇഷ്ടപ്പെടുന്നത്, ഉദാഹരണത്തിന് തെക്ക് അഭിമുഖമായുള്ള കല്ല് മതിലിന് എതിരായി.
ലിന്നിയ പാർവിഫോളിയ: മധ്യ ചൈന സ്വദേശിയായ കാപ്രിഫോളിയേസി കുടുംബത്തിലെ പൂച്ചെടികളുടെ ഒരു ഇനമാണ് ലിന്നിയ പാർവിഫോളിയ , അബെലിയ ഷുമാന്നി . 2 മീറ്റർ (7 അടി) ഉയരത്തിൽ 3 മീറ്റർ (10 അടി) വീതിയിൽ വളരുന്ന അർദ്ധ നിത്യഹരിത കുറ്റിച്ചെടിയാണിത്. ചുവന്ന കാലിസുള്ള പിങ്ക് പൂക്കൾ വേനൽക്കാലത്തിന്റെ അവസാനത്തിലും ശരത്കാലത്തും ഉത്പാദിപ്പിക്കപ്പെടുന്നു.
സാബെലിയ ത്യാഹിയോണി: സുഗന്ധമുള്ള അബെലിയ എന്നറിയപ്പെടുന്ന അബെലിയ മൊസാനെൻസിസ് എന്ന പര്യായമായ സബേലിയ ടിയാഹിയോണി , ഹണിസക്കിൾ കുടുംബത്തിലെ കാപ്രിഫോളിയേസിയിലെ ഇലപൊഴിക്കുന്ന കുറ്റിച്ചെടിയാണ്. 2 മീറ്റർ ഉയരത്തിലും വീതിയിലും വളരുന്ന ഇത് പല അനുബന്ധ ഇനങ്ങളേക്കാളും കഠിനമാണ്, താപനില −20 ° C (−4 ° F) വരെ കുറവാണ്. ട്യൂബുലാർ പൂക്കൾ പിങ്ക് കലർന്ന വെളുത്തതും വളരെ സുഗന്ധമുള്ളതുമാണ്, വസന്തത്തിന്റെ അവസാനത്തിൽ പ്രത്യക്ഷപ്പെടുന്നു. തിളങ്ങുന്ന പച്ച ഇലകൾ വീഴുന്നതിന് മുമ്പ് ശരത്കാലത്തിലാണ് ചുവപ്പായി മാറുന്നത്.
ലിന്നിയ പാർവിഫോളിയ: മധ്യ ചൈന സ്വദേശിയായ കാപ്രിഫോളിയേസി കുടുംബത്തിലെ പൂച്ചെടികളുടെ ഒരു ഇനമാണ് ലിന്നിയ പാർവിഫോളിയ , അബെലിയ ഷുമാന്നി . 2 മീറ്റർ (7 അടി) ഉയരത്തിൽ 3 മീറ്റർ (10 അടി) വീതിയിൽ വളരുന്ന അർദ്ധ നിത്യഹരിത കുറ്റിച്ചെടിയാണിത്. ചുവന്ന കാലിസുള്ള പിങ്ക് പൂക്കൾ വേനൽക്കാലത്തിന്റെ അവസാനത്തിലും ശരത്കാലത്തും ഉത്പാദിപ്പിക്കപ്പെടുന്നു.
ലിന്നിയ × ഗ്രാൻഡിഫ്ലോറ: ലിന്നെഅ × ഗ്രാന്റിഫ്ളോറ, പര്യായ അബെലിഅ × ഗ്രാന്റിഫ്ളോറ, Honeysuckle കുടുംബം കാപ്രിഫോളിയേസി, എൽ ഉനിഫ്ലൊര കൂടെ എൽ ഛിനെംസിസ് ഹ്യ്ബ്രിദിസിന്ഗ് ഉന്നയിച്ച ചെടിയുടെ പൂവിടുമ്പോൾ ഒരു സങ്കരയിനത്തെ ആണ്.
ലിന്നിയ × ഗ്രാൻഡിഫ്ലോറ: ലിന്നെഅ × ഗ്രാന്റിഫ്ളോറ, പര്യായ അബെലിഅ × ഗ്രാന്റിഫ്ളോറ, Honeysuckle കുടുംബം കാപ്രിഫോളിയേസി, എൽ ഉനിഫ്ലൊര കൂടെ എൽ ഛിനെംസിസ് ഹ്യ്ബ്രിദിസിന്ഗ് ഉന്നയിച്ച ചെടിയുടെ പൂവിടുമ്പോൾ ഒരു സങ്കരയിനത്തെ ആണ്.
ലിന്നിയ × ഗ്രാൻഡിഫ്ലോറ: ലിന്നെഅ × ഗ്രാന്റിഫ്ളോറ, പര്യായ അബെലിഅ × ഗ്രാന്റിഫ്ളോറ, Honeysuckle കുടുംബം കാപ്രിഫോളിയേസി, എൽ ഉനിഫ്ലൊര കൂടെ എൽ ഛിനെംസിസ് ഹ്യ്ബ്രിദിസിന്ഗ് ഉന്നയിച്ച ചെടിയുടെ പൂവിടുമ്പോൾ ഒരു സങ്കരയിനത്തെ ആണ്.
അബെലിയൻ: അബെലിയൻ ഇനിപ്പറയുന്നവ പരാമർശിക്കാം:
അബെലിയൻ, ട ub ബെറിയൻ സിദ്ധാന്തങ്ങൾ: ഗണിതശാസ്ത്രത്തിൽ, ഒരേ ശ്രേണി നൽകുന്നതിന് വ്യത്യസ്ത ശ്രേണികളെ സംഗ്രഹിക്കുന്നതിനുള്ള രണ്ട് രീതികൾക്ക് വ്യവസ്ഥകൾ നൽകുന്ന സിദ്ധാന്തങ്ങളാണ് അബെലിയൻ, ട ub ബെറിയൻ സിദ്ധാന്തങ്ങൾ , നീൽസ് ഹെൻറിക് ആബെലിന്റെയും ആൽഫ്രഡ് ട ub ബറിന്റെയും പേരിലാണ് ഇത് അറിയപ്പെടുന്നത്. ഒരു ശ്രേണി ചില പരിധികളിലേക്ക് ഒത്തുചേരുന്നുവെങ്കിൽ അതിന്റെ ആബെൽ തുക ഒരേ പരിധിയാണെന്ന് കാണിക്കുന്ന ഹാബെലിന്റെ സിദ്ധാന്തമാണ് യഥാർത്ഥ ഉദാഹരണങ്ങൾ, ഒരു ശ്രേണിയുടെ ആബെൽ തുക നിലവിലുണ്ടെങ്കിൽ ഗുണകങ്ങൾ പര്യാപ്തമാണെങ്കിൽ സീരീസ് ആബെലിലേക്ക് സംയോജിക്കുന്നു തുക. കൂടുതൽ പൊതുവായ സംഗ്രഹ രീതികൾക്ക് കൂടുതൽ പൊതുവായ അബെലിയൻ, ട ub ബേറിയൻ സിദ്ധാന്തങ്ങൾ സമാന ഫലങ്ങൾ നൽകുന്നു.
അബെലിയൻ: അബെലിയൻ ഇനിപ്പറയുന്നവ പരാമർശിക്കാം:
അബെലിയൻ: അബെലിയൻ ഇനിപ്പറയുന്നവ പരാമർശിക്കാം:
അബെലിയൻ 2-ഗ്രൂപ്പ്: മാത്തമാറ്റിക്സിൽ, ഉയർന്ന ബീജഗണിതത്തിന്റെ അർത്ഥത്തിൽ, ഒരു ആബിലിയൻ ഗ്രൂപ്പിന്റെ ഉയർന്ന അളവിലുള്ള അനലോഗ് ആണ് അബെലിയൻ 2-ഗ്രൂപ്പ് , അലക്സാണ്ടർ ഗ്രോതെൻഡിക് ആദ്യം അവതരിപ്പിച്ചത്, അബേലിയൻ ഇനങ്ങളെയും പിക്കാർഡ് ഗ്രൂപ്പുകളെയും ചുറ്റിപ്പറ്റിയുള്ള അമൂർത്ത ഘടനകളെക്കുറിച്ച് പഠിക്കുന്നതിനിടയിലാണ്. കൂടുതൽ വ്യക്തമായി പറഞ്ഞാൽ, അവ നൽകുന്നത് ഗ്രൂപ്പോയിഡുകളാണ് അവയ്‌ക്ക് ഒരു ബൈഫങ്‌ക്ടർ ഉണ്ട് ഇത് ab ദ്യോഗികമായി ഒരു അബെലിയൻ ഗ്രൂപ്പിന്റെ കൂട്ടിച്ചേർക്കൽ പോലെ പ്രവർത്തിക്കുന്നു. അതായത്, ബൈഫങ്ക്റ്റർ കമ്മ്യൂട്ടറ്റിവിറ്റി, അസോസിയേറ്റിവിറ്റി, ഒരു ഐഡന്റിറ്റി ഘടന എന്നിവയെക്കുറിച്ചുള്ള ഒരു ആശയം ഉണ്ട്. ഇത് വളരെ ഉയർന്നതും അമൂർത്തവുമായ ഒരു ഘടനയാണെന്ന് തോന്നുമെങ്കിലും, ഹാബെലിയൻ 2-ഗ്രൂപ്പുകൾക്ക് നിരവധി ഉദാഹരണങ്ങളുണ്ട്. വാസ്തവത്തിൽ, അവയിൽ ചിലത് ഉയർന്ന ബീജഗണിത ഘടനകളുടെ സങ്കീർണ്ണമായ ഉദാഹരണങ്ങൾക്ക് പ്രോട്ടോടൈപ്പുകൾ നൽകുന്നു, അബെലിയൻ എൻ-ഗ്രൂപ്പുകൾ.
അബെലിയൻ വിഭാഗം: ഗണിതശാസ്ത്രത്തിൽ ഒരു ക്രമഗ്രൂപ്പ് വിഭാഗം മൊര്ഫിസ്മ്സ് ആൻഡ് വസ്തുക്കൾ ചേർത്തു കഴിയുന്ന ഒപ്പം അതിൽ കെര്ണലുകളും ചൊകെര്നെല്സ് നിലവിലില്ല സമ്മോഹന ഗുണങ്ങളാണ് ഒരു വിഭാഗം ആണ്. ഒരു ഹീലിയൻ വിഭാഗത്തിന്റെ പ്രചോദനാത്മക പ്രോട്ടോടൈപ്പിക്കൽ ഉദാഹരണം അബെലിയൻ ഗ്രൂപ്പുകളുടെ വിഭാഗമാണ്, അബ് . അലക്സാണ്ടർ ഗ്രോതെൻഡിക്കിന്റെ നിരവധി കോഹമോളജി സിദ്ധാന്തങ്ങളെ ഏകീകരിക്കാനുള്ള ശ്രമത്തിലാണ് ഈ സിദ്ധാന്തം ഉത്ഭവിച്ചത്. അബെലിയൻ വിഭാഗങ്ങൾ വളരെ സ്ഥിരതയുള്ള വിഭാഗങ്ങളാണ്; ഉദാഹരണത്തിന് അവ പതിവായതിനാൽ പാമ്പ് ലെമ്മയെ തൃപ്തിപ്പെടുത്തുന്നു. നിരവധി വർ‌ഗ്ഗ നിർ‌മ്മാണങ്ങൾ‌ക്ക് കീഴിൽ അബെലിയൻ‌ വിഭാഗങ്ങളുടെ ക്ലാസ് അടച്ചിരിക്കുന്നു, ഉദാഹരണത്തിന്, ഒരു അബെലിയൻ‌ വിഭാഗത്തിലെ ചെയിൻ‌ കോംപ്ലക്സുകളുടെ വിഭാഗം, അല്ലെങ്കിൽ‌ ഒരു ചെറിയ വിഭാഗം മുതൽ‌ ഒരു അബെലിയൻ‌ വിഭാഗം വരെയുള്ള ഫംഗ്‌റ്ററുകൾ‌ എന്നിവ അബെലിയൻ‌ വിഭാഗമാണ്. ഈ സ്ഥിരത സവിശേഷതകൾ അവയെ ഹോമോളജിക്കൽ ആൾജിബ്രയിലും അതിനപ്പുറത്തും അനിവാര്യമാക്കുന്നു; ബീജഗണിത ജ്യാമിതി, കോഹമോളജി, ശുദ്ധ കാറ്റഗറി സിദ്ധാന്തം എന്നിവയിൽ സിദ്ധാന്തത്തിന് പ്രധാന പ്രയോഗങ്ങളുണ്ട്. നീൽ‌സ് ഹെൻ‌റിക് ആബെലിന്റെ പേരിലാണ് അബെലിയൻ‌ വിഭാഗങ്ങൾ‌.
ആദ്യ തരത്തിലുള്ള വ്യത്യാസം: ഗണിതശാസ്ത്രത്തിൽ, റൈമാൻ ഉപരിതലങ്ങളുടെയും ബീജഗണിത വക്രങ്ങളുടെയും സിദ്ധാന്തങ്ങളിൽ എല്ലായിടത്തും-പതിവ് ഡിഫറൻഷ്യൽ 1-ഫോമുകൾക്കായി ഉപയോഗിക്കുന്ന പരമ്പരാഗത പദമാണ് ആദ്യ തരത്തിലുള്ള വ്യത്യാസം. ഒരു സങ്കീർണ്ണമായ പെരുകിയിരിക്കുന്നു എം നൽകിയിരിക്കുന്ന, ഒന്നാമത്തെ വിഭാഗത്തിൽ ω ഒരു ഡിഫറൻഷ്യൽ അതിനാൽ എല്ലായിടത്തും ഹൊലൊമൊര്ഫിച് ഒരു 1-ഫോം അതേ കാര്യം; ബീജഗണിത വൈവിധ്യമാർന്ന V- യിൽ , ഏകവചനമല്ലാത്ത ഇത് കോഹ്ലർ ഡിഫറൻഷ്യലുകളുടെ ഏകീകൃത ഷീഫ് Ω 1 ന്റെ ആഗോള വിഭാഗമായിരിക്കും. രണ്ടായാലും നിർവചനത്തിന്റെ ഉത്ഭവം അബെലിയൻ ഇന്റഗ്രൽ സിദ്ധാന്തത്തിലാണ്.
അബെലിയൻ വിപുലീകരണം: അമൂർത്ത ബീജഗണിതത്തിൽ, ഒരു ഗാലോയിസ് എക്സ്റ്റൻഷനാണ് അബെലിയൻ എക്സ്റ്റൻഷൻ, ഇതിന്റെ ഗാലോയിസ് ഗ്രൂപ്പ് അബെലിയൻ ആണ്. ഗാലോയിസ് ഗ്രൂപ്പും ചാക്രികമാകുമ്പോൾ, വിപുലീകരണത്തെ ചാക്രിക വിപുലീകരണം എന്നും വിളിക്കുന്നു. മറ്റൊരു ദിശയിലേക്ക് പോകുമ്പോൾ, ഒരു ഗാലോയിസ് എക്സ്റ്റൻഷനെ അതിന്റെ ഗലോയിസ് ഗ്രൂപ്പ് പരിഹരിക്കാവുന്നതാണെങ്കിൽ പരിഹരിക്കാവുന്നവ എന്ന് വിളിക്കുന്നു, അതായത്, ഗ്രൂപ്പിനെ ഒരു അബിലിയൻ ഗ്രൂപ്പിന്റെ സാധാരണ എക്സ്റ്റെൻഷനുകളുടെ ഒരു പരമ്പരയായി വിഘടിപ്പിക്കാൻ കഴിയുമെങ്കിൽ.
അബെലിയൻ ഇനം: ഗണിതശാസ്ത്രത്തിൽ, പ്രത്യേകിച്ച് ബീജീയജ്യാമിതി, സങ്കീർണ്ണമായ വിശകലനം ബീജീയ എണ്ണം തിയറി, ഒരു ക്രമഗ്രൂപ്പ് മുറികൾ ഒരു ബീജീയ ഗ്രൂപ്പ് ഒരു പ്രൊജെച്തിവെ ബീജീയ വൈവിധ്യം, അതായത്, പതിവ് പ്രവർത്തനങ്ങൾ തിരിക്കാം കഴിയുന്ന ഒരു ഗ്രൂപ്പ് നിയമം ഉണ്ട്. ബീജഗണിത ജ്യാമിതിയിലും ബീജഗണിത ജ്യാമിതിയിലും സംഖ്യ സിദ്ധാന്തത്തിലും മറ്റ് വിഷയങ്ങളെക്കുറിച്ചുള്ള കൂടുതൽ ഗവേഷണങ്ങൾക്ക് ഒഴിച്ചുകൂടാനാവാത്ത ഉപകരണങ്ങളിൽ അബെലിയൻ ഇനങ്ങൾ ഒരേ സമയം ഉൾപ്പെടുന്നു.
അബെലിയൻ ഗ്രൂപ്പ്: ഗണിതശാസ്ത്രത്തിൽ, ഒരു ഗ്രൂപ്പ് ഗ്രൂപ്പിനെ ഒരു കമ്മ്യൂട്ടേറ്റീവ് ഗ്രൂപ്പ് എന്നും വിളിക്കുന്നു, അതിൽ ഗ്രൂപ്പ് പ്രവർത്തനം രണ്ട് ഗ്രൂപ്പ് ഘടകങ്ങളിൽ പ്രയോഗിക്കുന്നതിന്റെ ഫലം അവ എഴുതിയ ക്രമത്തെ ആശ്രയിക്കുന്നില്ല. അതായത്, ഗ്രൂപ്പ് പ്രവർത്തനം കമ്മ്യൂട്ടേറ്റീവ് ആണ്. ഒരു പ്രവർത്തനമെന്ന നിലയിൽ, പൂർണ്ണസംഖ്യകളും യഥാർത്ഥ സംഖ്യകളും അബെലിയൻ ഗ്രൂപ്പുകളായി മാറുന്നു, കൂടാതെ ഒരു ഹീലിയൻ ഗ്രൂപ്പിന്റെ ആശയം ഈ ഉദാഹരണങ്ങളുടെ പൊതുവൽക്കരണമായി കാണപ്പെടാം. പത്തൊൻപതാം നൂറ്റാണ്ടിന്റെ തുടക്കത്തിൽ ഗണിതശാസ്ത്രജ്ഞനായ നീൽസ് ഹെൻറിക് ആബെലിന്റെ പേരിലാണ് അബെലിയൻ ഗ്രൂപ്പുകൾക്ക് പേര് നൽകിയിരിക്കുന്നത്.
ഹിഗ്സ് സംവിധാനം: കണിക ഭൗതികശാസ്ത്രത്തിന്റെ സ്റ്റാൻഡേർഡ് മോഡലിൽ, ഗേജ് ബോസോണുകളുടെ "പിണ്ഡം" എന്ന സ്വത്തിന്റെ ഉത്പാദന സംവിധാനം വിശദീകരിക്കാൻ ഹിഗ്സ് സംവിധാനം അനിവാര്യമാണ്. ഹിഗ്സ് സംവിധാനം ഇല്ലാതെ, എല്ലാ ബോസോണുകളും (രണ്ട് തരം കണികകളിൽ ഒന്ന്, മറ്റൊന്ന് ഫെർമിയനുകൾ) പിണ്ഡമില്ലാത്തതായി കണക്കാക്കും, പക്ഷേ അളവുകൾ കാണിക്കുന്നത് W + , W - , Z 0 ബോസോണുകൾക്ക് യഥാർത്ഥത്തിൽ 80 GeV ന്റെ വലിയ പിണ്ഡമുണ്ടെന്ന് / സി 2 . ഹിഗ്സ് ഫീൽഡ് ഈ ക und ണ്ട്രം പരിഹരിക്കുന്നു. മെക്കാനിസത്തിന്റെ ഏറ്റവും ലളിതമായ വിവരണം ഒരു ക്വാണ്ടം ഫീൽഡ് (ഹിഗ്സ് ഫീൽഡ്) ചേർക്കുന്നു, അത് സ്റ്റാൻഡേർഡ് മോഡലിലേക്ക് എല്ലാ സ്ഥലവും വ്യാപിക്കുന്നു. വളരെ ഉയർന്ന ചില താപനിലയ്ക്ക് താഴെ, ഫീൽഡ് പ്രതിപ്രവർത്തന സമയത്ത് സ്വതവേയുള്ള സമമിതി തകരാൻ കാരണമാകുന്നു. സമമിതിയുടെ തകർച്ച ഹിഗ്സ് സംവിധാനത്തെ പ്രേരിപ്പിക്കുന്നു, ഇത് സംവദിക്കുന്ന ബോസോണുകൾക്ക് പിണ്ഡമുണ്ടാക്കുന്നു. സ്റ്റാൻഡേർഡ് മോഡൽ, വാക്യം "ഹിഗ്സ് മെക്കാനിസം" വൈദ്യുതദുർബല സമമിതി ബ്രേക്കിംഗ് വഴി പ ± വേണ്ടി ബഹുജനങ്ങളെ, Z ദുർബലമായ ഗേജ് ബോസോണുകൾ തലമുറയോടു വ്യക്തമായി സൂചിപ്പിക്കുന്നു. CERN- ലെ ലാർജ് ഹാഡ്രോൺ കൊളൈഡർ വളരെ സാധ്യത ഉണ്ടാക്കുന്ന വയലിൽ, അല്ലെങ്കിൽ പോലെ ഒരു, നിലവിലുണ്ട് എന്നും ഹിഗ്സ് മെക്കാനിസം പ്രകൃതിയിൽ നടക്കുന്നത് എങ്ങനെ വിശദീകരിക്കുന്ന, 14 മാർച്ച് 2013 ഹിഗ്സ് കണികാ നിലയുമായി ഫലങ്ങൾ പ്രഖ്യാപിച്ചു.
ഹിഗ്സ് സംവിധാനം: കണിക ഭൗതികശാസ്ത്രത്തിന്റെ സ്റ്റാൻഡേർഡ് മോഡലിൽ, ഗേജ് ബോസോണുകളുടെ "പിണ്ഡം" എന്ന സ്വത്തിന്റെ ഉത്പാദന സംവിധാനം വിശദീകരിക്കാൻ ഹിഗ്സ് സംവിധാനം അനിവാര്യമാണ്. ഹിഗ്സ് സംവിധാനം ഇല്ലാതെ, എല്ലാ ബോസോണുകളും (രണ്ട് തരം കണികകളിൽ ഒന്ന്, മറ്റൊന്ന് ഫെർമിയനുകൾ) പിണ്ഡമില്ലാത്തതായി കണക്കാക്കും, പക്ഷേ അളവുകൾ കാണിക്കുന്നത് W + , W - , Z 0 ബോസോണുകൾക്ക് യഥാർത്ഥത്തിൽ 80 GeV ന്റെ വലിയ പിണ്ഡമുണ്ടെന്ന് / സി 2 . ഹിഗ്സ് ഫീൽഡ് ഈ ക und ണ്ട്രം പരിഹരിക്കുന്നു. മെക്കാനിസത്തിന്റെ ഏറ്റവും ലളിതമായ വിവരണം ഒരു ക്വാണ്ടം ഫീൽഡ് (ഹിഗ്സ് ഫീൽഡ്) ചേർക്കുന്നു, അത് സ്റ്റാൻഡേർഡ് മോഡലിലേക്ക് എല്ലാ സ്ഥലവും വ്യാപിക്കുന്നു. വളരെ ഉയർന്ന ചില താപനിലയ്ക്ക് താഴെ, ഫീൽഡ് പ്രതിപ്രവർത്തന സമയത്ത് സ്വതവേയുള്ള സമമിതി തകരാൻ കാരണമാകുന്നു. സമമിതിയുടെ തകർച്ച ഹിഗ്സ് സംവിധാനത്തെ പ്രേരിപ്പിക്കുന്നു, ഇത് സംവദിക്കുന്ന ബോസോണുകൾക്ക് പിണ്ഡമുണ്ടാക്കുന്നു. സ്റ്റാൻഡേർഡ് മോഡൽ, വാക്യം "ഹിഗ്സ് മെക്കാനിസം" വൈദ്യുതദുർബല സമമിതി ബ്രേക്കിംഗ് വഴി പ ± വേണ്ടി ബഹുജനങ്ങളെ, Z ദുർബലമായ ഗേജ് ബോസോണുകൾ തലമുറയോടു വ്യക്തമായി സൂചിപ്പിക്കുന്നു. CERN- ലെ ലാർജ് ഹാഡ്രോൺ കൊളൈഡർ വളരെ സാധ്യത ഉണ്ടാക്കുന്ന വയലിൽ, അല്ലെങ്കിൽ പോലെ ഒരു, നിലവിലുണ്ട് എന്നും ഹിഗ്സ് മെക്കാനിസം പ്രകൃതിയിൽ നടക്കുന്നത് എങ്ങനെ വിശദീകരിക്കുന്ന, 14 മാർച്ച് 2013 ഹിഗ്സ് കണികാ നിലയുമായി ഫലങ്ങൾ പ്രഖ്യാപിച്ചു.
അബെലിയൻ ഇന്റഗ്രൽ: ഗണിതശാസ്ത്രത്തിൽ, നോർവീജിയൻ ഗണിതശാസ്ത്രജ്ഞനായ നീൽസ് ഹെൻറിക് ആബെലിന്റെ പേരിലുള്ള ഒരു അബെലിയൻ ഇന്റഗ്രൽ , രൂപത്തിന്റെ സങ്കീർണ്ണ തലത്തിൽ ഒരു അവിഭാജ്യ ഘടകമാണ്
ബീജഗണിതം: ഗണിതശാസ്ത്രത്തിൽ, ഒരു ലൈ ആൾജിബ്ര ഒരു വെക്റ്റർ സ്പേസ് ആണ് ഒന്നിടവിട്ട ബിലിനിയർ മാപ്പ്, ലൈ ബ്രാക്കറ്റ് എന്ന ഓപ്പറേഷനുമായി , അത് ജേക്കബി ഐഡന്റിറ്റിയെ തൃപ്തിപ്പെടുത്തുന്നു. വെക്റ്റർ സ്പേസ് ഈ പ്രവർത്തനത്തോടൊപ്പം ഒരു നോൺ-അസ്സോക്കേറ്റീവ് ബീജഗണിതമാണ്, അതായത് ലൈ ബ്രാക്കറ്റ് അനുബന്ധമായിരിക്കണമെന്നില്ല.
അബെലിയൻ ലീ ഗ്രൂപ്പ്: ജ്യാമിതിയിൽ, ഒരു അബെലിയൻ ഗ്രൂപ്പാണ് ഒരു ലൈ ഗ്രൂപ്പാണ്.
ആബെൽ പോളിനോമിയലുകൾ: ഗണിതശാസ്ത്രത്തിലെ ആബെൽ പോളിനോമിയലുകൾ ഒരു പോളിനോമിയൽ സീക്വൻസായി മാറുന്നു, ഇതിന്റെ n- ാമത്തെ പദം രൂപത്തിലാണ്
അബെലിയൻ, ട ub ബെറിയൻ സിദ്ധാന്തങ്ങൾ: ഗണിതശാസ്ത്രത്തിൽ, ഒരേ ശ്രേണി നൽകുന്നതിന് വ്യത്യസ്ത ശ്രേണികളെ സംഗ്രഹിക്കുന്നതിനുള്ള രണ്ട് രീതികൾക്ക് വ്യവസ്ഥകൾ നൽകുന്ന സിദ്ധാന്തങ്ങളാണ് അബെലിയൻ, ട ub ബെറിയൻ സിദ്ധാന്തങ്ങൾ , നീൽസ് ഹെൻറിക് ആബെലിന്റെയും ആൽഫ്രഡ് ട ub ബറിന്റെയും പേരിലാണ് ഇത് അറിയപ്പെടുന്നത്. ഒരു ശ്രേണി ചില പരിധികളിലേക്ക് ഒത്തുചേരുന്നുവെങ്കിൽ അതിന്റെ ആബെൽ തുക ഒരേ പരിധിയാണെന്ന് കാണിക്കുന്ന ഹാബെലിന്റെ സിദ്ധാന്തമാണ് യഥാർത്ഥ ഉദാഹരണങ്ങൾ, ഒരു ശ്രേണിയുടെ ആബെൽ തുക നിലവിലുണ്ടെങ്കിൽ ഗുണകങ്ങൾ പര്യാപ്തമാണെങ്കിൽ സീരീസ് ആബെലിലേക്ക് സംയോജിക്കുന്നു തുക. കൂടുതൽ പൊതുവായ സംഗ്രഹ രീതികൾക്ക് കൂടുതൽ പൊതുവായ അബെലിയൻ, ട ub ബേറിയൻ സിദ്ധാന്തങ്ങൾ സമാന ഫലങ്ങൾ നൽകുന്നു.
അബെലിയൻ ഇനം: ഗണിതശാസ്ത്രത്തിൽ, പ്രത്യേകിച്ച് ബീജീയജ്യാമിതി, സങ്കീർണ്ണമായ വിശകലനം ബീജീയ എണ്ണം തിയറി, ഒരു ക്രമഗ്രൂപ്പ് മുറികൾ ഒരു ബീജീയ ഗ്രൂപ്പ് ഒരു പ്രൊജെച്തിവെ ബീജീയ വൈവിധ്യം, അതായത്, പതിവ് പ്രവർത്തനങ്ങൾ തിരിക്കാം കഴിയുന്ന ഒരു ഗ്രൂപ്പ് നിയമം ഉണ്ട്. ബീജഗണിത ജ്യാമിതിയിലും ബീജഗണിത ജ്യാമിതിയിലും സംഖ്യ സിദ്ധാന്തത്തിലും മറ്റ് വിഷയങ്ങളെക്കുറിച്ചുള്ള കൂടുതൽ ഗവേഷണങ്ങൾക്ക് ഒഴിച്ചുകൂടാനാവാത്ത ഉപകരണങ്ങളിൽ അബെലിയൻ ഇനങ്ങൾ ഒരേ സമയം ഉൾപ്പെടുന്നു.
അനുബന്ധ ബീജഗണിതം: ഗണിതശാസ്ത്രത്തിൽ, സങ്കലനം, ഗുണനം, ചില മേഖലയിലെ മൂലകങ്ങളുടെ സ്കെയിലർ ഗുണനം എന്നിവയുടെ അനുയോജ്യമായ പ്രവർത്തനങ്ങളുള്ള ഒരു ബീജഗണിത ഘടനയാണ് ഒരു അനുബന്ധ ബീജഗണിതം . പുറമെ വലയ ഒരുമിച്ച് ഒരു ഒരു മോതിരം ഘടന തരും; പുറമേ ഭൌമമായ വലയ ഒരുമിച്ച് ഒരു കെ ഒരു വെക്റ്റർ സ്ഥലം ഘടന തരും. ഈ ലേഖനത്തിൽ നാം വയലിൽ കെ മേൽ ഒരു അഷൊചിഅതിവെ ബീജഗണിതം അർഥം പദം കെ -അല്ഗെബ്ര ഉപയോഗിക്കും. കെ- ആൽ‌ജിബ്രയുടെ ഒരു സ്റ്റാൻ‌ഡേർഡ് ആദ്യ ഉദാഹരണം സാധാരണ ഫീൽ‌ഡ് മാട്രിക്സ് ഗുണനത്തോടുകൂടിയ കെ ഫീൽ‌ഡിന് മുകളിലുള്ള ചതുര മാട്രിക്സുകളുടെ ഒരു മോതിരം.
അബെലിയൻ, ട ub ബെറിയൻ സിദ്ധാന്തങ്ങൾ: ഗണിതശാസ്ത്രത്തിൽ, ഒരേ ശ്രേണി നൽകുന്നതിന് വ്യത്യസ്ത ശ്രേണികളെ സംഗ്രഹിക്കുന്നതിനുള്ള രണ്ട് രീതികൾക്ക് വ്യവസ്ഥകൾ നൽകുന്ന സിദ്ധാന്തങ്ങളാണ് അബെലിയൻ, ട ub ബെറിയൻ സിദ്ധാന്തങ്ങൾ , നീൽസ് ഹെൻറിക് ആബെലിന്റെയും ആൽഫ്രഡ് ട ub ബറിന്റെയും പേരിലാണ് ഇത് അറിയപ്പെടുന്നത്. ഒരു ശ്രേണി ചില പരിധികളിലേക്ക് ഒത്തുചേരുന്നുവെങ്കിൽ അതിന്റെ ആബെൽ തുക ഒരേ പരിധിയാണെന്ന് കാണിക്കുന്ന ഹാബെലിന്റെ സിദ്ധാന്തമാണ് യഥാർത്ഥ ഉദാഹരണങ്ങൾ, ഒരു ശ്രേണിയുടെ ആബെൽ തുക നിലവിലുണ്ടെങ്കിൽ ഗുണകങ്ങൾ പര്യാപ്തമാണെങ്കിൽ സീരീസ് ആബെലിലേക്ക് സംയോജിക്കുന്നു തുക. കൂടുതൽ പൊതുവായ സംഗ്രഹ രീതികൾക്ക് കൂടുതൽ പൊതുവായ അബെലിയൻ, ട ub ബേറിയൻ സിദ്ധാന്തങ്ങൾ സമാന ഫലങ്ങൾ നൽകുന്നു.
അബെലിയൻ, ട ub ബെറിയൻ സിദ്ധാന്തങ്ങൾ: ഗണിതശാസ്ത്രത്തിൽ, ഒരേ ശ്രേണി നൽകുന്നതിന് വ്യത്യസ്ത ശ്രേണികളെ സംഗ്രഹിക്കുന്നതിനുള്ള രണ്ട് രീതികൾക്ക് വ്യവസ്ഥകൾ നൽകുന്ന സിദ്ധാന്തങ്ങളാണ് അബെലിയൻ, ട ub ബെറിയൻ സിദ്ധാന്തങ്ങൾ , നീൽസ് ഹെൻറിക് ആബെലിന്റെയും ആൽഫ്രഡ് ട ub ബറിന്റെയും പേരിലാണ് ഇത് അറിയപ്പെടുന്നത്. ഒരു ശ്രേണി ചില പരിധികളിലേക്ക് ഒത്തുചേരുന്നുവെങ്കിൽ അതിന്റെ ആബെൽ തുക ഒരേ പരിധിയാണെന്ന് കാണിക്കുന്ന ഹാബെലിന്റെ സിദ്ധാന്തമാണ് യഥാർത്ഥ ഉദാഹരണങ്ങൾ, ഒരു ശ്രേണിയുടെ ആബെൽ തുക നിലവിലുണ്ടെങ്കിൽ ഗുണകങ്ങൾ പര്യാപ്തമാണെങ്കിൽ സീരീസ് ആബെലിലേക്ക് സംയോജിക്കുന്നു തുക. കൂടുതൽ പൊതുവായ സംഗ്രഹ രീതികൾക്ക് കൂടുതൽ പൊതുവായ അബെലിയൻ, ട ub ബേറിയൻ സിദ്ധാന്തങ്ങൾ സമാന ഫലങ്ങൾ നൽകുന്നു.
അബെലിയൻ വിഭാഗം: ഗണിതശാസ്ത്രത്തിൽ ഒരു ക്രമഗ്രൂപ്പ് വിഭാഗം മൊര്ഫിസ്മ്സ് ആൻഡ് വസ്തുക്കൾ ചേർത്തു കഴിയുന്ന ഒപ്പം അതിൽ കെര്ണലുകളും ചൊകെര്നെല്സ് നിലവിലില്ല സമ്മോഹന ഗുണങ്ങളാണ് ഒരു വിഭാഗം ആണ്. ഒരു ഹീലിയൻ വിഭാഗത്തിന്റെ പ്രചോദനാത്മക പ്രോട്ടോടൈപ്പിക്കൽ ഉദാഹരണം അബെലിയൻ ഗ്രൂപ്പുകളുടെ വിഭാഗമാണ്, അബ് . അലക്സാണ്ടർ ഗ്രോതെൻഡിക്കിന്റെ നിരവധി കോഹമോളജി സിദ്ധാന്തങ്ങളെ ഏകീകരിക്കാനുള്ള ശ്രമത്തിലാണ് ഈ സിദ്ധാന്തം ഉത്ഭവിച്ചത്. അബെലിയൻ വിഭാഗങ്ങൾ വളരെ സ്ഥിരതയുള്ള വിഭാഗങ്ങളാണ്; ഉദാഹരണത്തിന് അവ പതിവായതിനാൽ പാമ്പ് ലെമ്മയെ തൃപ്തിപ്പെടുത്തുന്നു. നിരവധി വർ‌ഗ്ഗ നിർ‌മ്മാണങ്ങൾ‌ക്ക് കീഴിൽ അബെലിയൻ‌ വിഭാഗങ്ങളുടെ ക്ലാസ് അടച്ചിരിക്കുന്നു, ഉദാഹരണത്തിന്, ഒരു അബെലിയൻ‌ വിഭാഗത്തിലെ ചെയിൻ‌ കോംപ്ലക്സുകളുടെ വിഭാഗം, അല്ലെങ്കിൽ‌ ഒരു ചെറിയ വിഭാഗം മുതൽ‌ ഒരു അബെലിയൻ‌ വിഭാഗം വരെയുള്ള ഫംഗ്‌റ്ററുകൾ‌ എന്നിവ അബെലിയൻ‌ വിഭാഗമാണ്. ഈ സ്ഥിരത സവിശേഷതകൾ അവയെ ഹോമോളജിക്കൽ ആൾജിബ്രയിലും അതിനപ്പുറത്തും അനിവാര്യമാക്കുന്നു; ബീജഗണിത ജ്യാമിതി, കോഹമോളജി, ശുദ്ധ കാറ്റഗറി സിദ്ധാന്തം എന്നിവയിൽ സിദ്ധാന്തത്തിന് പ്രധാന പ്രയോഗങ്ങളുണ്ട്. നീൽ‌സ് ഹെൻ‌റിക് ആബെലിന്റെ പേരിലാണ് അബെലിയൻ‌ വിഭാഗങ്ങൾ‌.
അബെലിയൻ വിഭാഗം: ഗണിതശാസ്ത്രത്തിൽ ഒരു ക്രമഗ്രൂപ്പ് വിഭാഗം മൊര്ഫിസ്മ്സ് ആൻഡ് വസ്തുക്കൾ ചേർത്തു കഴിയുന്ന ഒപ്പം അതിൽ കെര്ണലുകളും ചൊകെര്നെല്സ് നിലവിലില്ല സമ്മോഹന ഗുണങ്ങളാണ് ഒരു വിഭാഗം ആണ്. ഒരു ഹീലിയൻ വിഭാഗത്തിന്റെ പ്രചോദനാത്മക പ്രോട്ടോടൈപ്പിക്കൽ ഉദാഹരണം അബെലിയൻ ഗ്രൂപ്പുകളുടെ വിഭാഗമാണ്, അബ് . അലക്സാണ്ടർ ഗ്രോതെൻഡിക്കിന്റെ നിരവധി കോഹമോളജി സിദ്ധാന്തങ്ങളെ ഏകീകരിക്കാനുള്ള ശ്രമത്തിലാണ് ഈ സിദ്ധാന്തം ഉത്ഭവിച്ചത്. അബെലിയൻ വിഭാഗങ്ങൾ വളരെ സ്ഥിരതയുള്ള വിഭാഗങ്ങളാണ്; ഉദാഹരണത്തിന് അവ പതിവായതിനാൽ പാമ്പ് ലെമ്മയെ തൃപ്തിപ്പെടുത്തുന്നു. നിരവധി വർ‌ഗ്ഗ നിർ‌മ്മാണങ്ങൾ‌ക്ക് കീഴിൽ അബെലിയൻ‌ വിഭാഗങ്ങളുടെ ക്ലാസ് അടച്ചിരിക്കുന്നു, ഉദാഹരണത്തിന്, ഒരു അബെലിയൻ‌ വിഭാഗത്തിലെ ചെയിൻ‌ കോംപ്ലക്സുകളുടെ വിഭാഗം, അല്ലെങ്കിൽ‌ ഒരു ചെറിയ വിഭാഗം മുതൽ‌ ഒരു അബെലിയൻ‌ വിഭാഗം വരെയുള്ള ഫംഗ്‌റ്ററുകൾ‌ എന്നിവ അബെലിയൻ‌ വിഭാഗമാണ്. ഈ സ്ഥിരത സവിശേഷതകൾ അവയെ ഹോമോളജിക്കൽ ആൾജിബ്രയിലും അതിനപ്പുറത്തും അനിവാര്യമാക്കുന്നു; ബീജഗണിത ജ്യാമിതി, കോഹമോളജി, ശുദ്ധ കാറ്റഗറി സിദ്ധാന്തം എന്നിവയിൽ സിദ്ധാന്തത്തിന് പ്രധാന പ്രയോഗങ്ങളുണ്ട്. നീൽ‌സ് ഹെൻ‌റിക് ആബെലിന്റെ പേരിലാണ് അബെലിയൻ‌ വിഭാഗങ്ങൾ‌.
സങ്കീർണ്ണ പ്രവർത്തനം: കമ്പ്യൂട്ടർ സയൻസിൽ, ഒരു സ്‌ട്രിംഗിന്റെ സങ്കീർണ്ണമായ പ്രവർത്തനം , ചില അക്ഷരമാലയിൽ നിന്നുള്ള പരിമിതമോ അനന്തമോ ആയ അക്ഷരങ്ങൾ, ആ സ്‌ട്രിംഗിൽ നിന്ന് വ്യത്യസ്തമായ ഘടകങ്ങളുടെ എണ്ണം കണക്കാക്കുന്ന പ്രവർത്തനമാണ്. കൂടുതൽ സാധാരണമായി, ഒരു ഭാഷയുടെ സങ്കീർണ്ണമായ പ്രവർത്തനം, ഒരു അക്ഷരമാലയ്‌ക്ക് മുകളിലുള്ള പരിമിതമായ പദങ്ങളുടെ ഒരു കൂട്ടം, നൽകിയിരിക്കുന്ന നീളത്തിന്റെ വ്യത്യസ്‌ത പദങ്ങളുടെ എണ്ണം കണക്കാക്കുന്നു.
കവറിംഗ് ഗ്രൂപ്പ്: ഗണിതശാസ്ത്രത്തിൽ ഗുണനവും എച്ച് ഒരു മൂടി ഗ്രൂപ്പിൽ എച്ച് ഒരു മൂടി സ്ഥലം ജി ആണ് ജി ഗുണനവും വകയുണ്ടെങ്കിൽ മാപ്പ് പി എന്ന്: G → H, തുടർച്ചയായ ഗ്രൂപ്പ് സമാംഗരൂപതയാകാനുള്ള. മാപ്പ് പി യെ കവറിംഗ് ഹോമോമോണിസം എന്ന് വിളിക്കുന്നു. പതിവായി സംഭവിക്കുന്ന ഒരു കേസ് ഇരട്ട കവറിംഗ് ഗ്രൂപ്പാണ് , ടോപ്പോളജിക്കൽ ഇരട്ട കവർ, അതിൽ H ന് ജിയിൽ സൂചിക 2 ഉണ്ട്; ഉദാഹരണങ്ങളിൽ സ്പിൻ ഗ്രൂപ്പുകൾ, പിൻ ഗ്രൂപ്പുകൾ, മെറ്റാപ്ലെക്റ്റിക് ഗ്രൂപ്പുകൾ എന്നിവ ഉൾപ്പെടുന്നു.
ആദ്യ തരത്തിലുള്ള വ്യത്യാസം: ഗണിതശാസ്ത്രത്തിൽ, റൈമാൻ ഉപരിതലങ്ങളുടെയും ബീജഗണിത വക്രങ്ങളുടെയും സിദ്ധാന്തങ്ങളിൽ എല്ലായിടത്തും-പതിവ് ഡിഫറൻഷ്യൽ 1-ഫോമുകൾക്കായി ഉപയോഗിക്കുന്ന പരമ്പരാഗത പദമാണ് ആദ്യ തരത്തിലുള്ള വ്യത്യാസം. ഒരു സങ്കീർണ്ണമായ പെരുകിയിരിക്കുന്നു എം നൽകിയിരിക്കുന്ന, ഒന്നാമത്തെ വിഭാഗത്തിൽ ω ഒരു ഡിഫറൻഷ്യൽ അതിനാൽ എല്ലായിടത്തും ഹൊലൊമൊര്ഫിച് ഒരു 1-ഫോം അതേ കാര്യം; ബീജഗണിത വൈവിധ്യമാർന്ന V- യിൽ , ഏകവചനമല്ലാത്ത ഇത് കോഹ്ലർ ഡിഫറൻഷ്യലുകളുടെ ഏകീകൃത ഷീഫ് Ω 1 ന്റെ ആഗോള വിഭാഗമായിരിക്കും. രണ്ടായാലും നിർവചനത്തിന്റെ ഉത്ഭവം അബെലിയൻ ഇന്റഗ്രൽ സിദ്ധാന്തത്തിലാണ്.
അബെലിയൻ വിപുലീകരണം: അമൂർത്ത ബീജഗണിതത്തിൽ, ഒരു ഗാലോയിസ് എക്സ്റ്റൻഷനാണ് അബെലിയൻ എക്സ്റ്റൻഷൻ, ഇതിന്റെ ഗാലോയിസ് ഗ്രൂപ്പ് അബെലിയൻ ആണ്. ഗാലോയിസ് ഗ്രൂപ്പും ചാക്രികമാകുമ്പോൾ, വിപുലീകരണത്തെ ചാക്രിക വിപുലീകരണം എന്നും വിളിക്കുന്നു. മറ്റൊരു ദിശയിലേക്ക് പോകുമ്പോൾ, ഒരു ഗാലോയിസ് എക്സ്റ്റൻഷനെ അതിന്റെ ഗലോയിസ് ഗ്രൂപ്പ് പരിഹരിക്കാവുന്നതാണെങ്കിൽ പരിഹരിക്കാവുന്നവ എന്ന് വിളിക്കുന്നു, അതായത്, ഗ്രൂപ്പിനെ ഒരു അബിലിയൻ ഗ്രൂപ്പിന്റെ സാധാരണ എക്സ്റ്റെൻഷനുകളുടെ ഒരു പരമ്പരയായി വിഘടിപ്പിക്കാൻ കഴിയുമെങ്കിൽ.
അബെലിയൻ വിപുലീകരണം: അമൂർത്ത ബീജഗണിതത്തിൽ, ഒരു ഗാലോയിസ് എക്സ്റ്റൻഷനാണ് അബെലിയൻ എക്സ്റ്റൻഷൻ, ഇതിന്റെ ഗാലോയിസ് ഗ്രൂപ്പ് അബെലിയൻ ആണ്. ഗാലോയിസ് ഗ്രൂപ്പും ചാക്രികമാകുമ്പോൾ, വിപുലീകരണത്തെ ചാക്രിക വിപുലീകരണം എന്നും വിളിക്കുന്നു. മറ്റൊരു ദിശയിലേക്ക് പോകുമ്പോൾ, ഒരു ഗാലോയിസ് എക്സ്റ്റൻഷനെ അതിന്റെ ഗലോയിസ് ഗ്രൂപ്പ് പരിഹരിക്കാവുന്നതാണെങ്കിൽ പരിഹരിക്കാവുന്നവ എന്ന് വിളിക്കുന്നു, അതായത്, ഗ്രൂപ്പിനെ ഒരു അബിലിയൻ ഗ്രൂപ്പിന്റെ സാധാരണ എക്സ്റ്റെൻഷനുകളുടെ ഒരു പരമ്പരയായി വിഘടിപ്പിക്കാൻ കഴിയുമെങ്കിൽ.
അബെലിയൻ ഇനം: ഗണിതശാസ്ത്രത്തിൽ, പ്രത്യേകിച്ച് ബീജീയജ്യാമിതി, സങ്കീർണ്ണമായ വിശകലനം ബീജീയ എണ്ണം തിയറി, ഒരു ക്രമഗ്രൂപ്പ് മുറികൾ ഒരു ബീജീയ ഗ്രൂപ്പ് ഒരു പ്രൊജെച്തിവെ ബീജീയ വൈവിധ്യം, അതായത്, പതിവ് പ്രവർത്തനങ്ങൾ തിരിക്കാം കഴിയുന്ന ഒരു ഗ്രൂപ്പ് നിയമം ഉണ്ട്. ബീജഗണിത ജ്യാമിതിയിലും ബീജഗണിത ജ്യാമിതിയിലും സംഖ്യ സിദ്ധാന്തത്തിലും മറ്റ് വിഷയങ്ങളെക്കുറിച്ചുള്ള കൂടുതൽ ഗവേഷണങ്ങൾക്ക് ഒഴിച്ചുകൂടാനാവാത്ത ഉപകരണങ്ങളിൽ അബെലിയൻ ഇനങ്ങൾ ഒരേ സമയം ഉൾപ്പെടുന്നു.
ഗേജ് സിദ്ധാന്തം: ഭൗതികശാസ്ത്രത്തിൽ, ഗേജ് തിയറി എന്നത് ഒരു തരം ഫീൽഡ് സിദ്ധാന്തമാണ്, അതിൽ ചില ലീ ഗ്രൂപ്പുകളിൽ നിന്നുള്ള പ്രാദേശിക പരിവർത്തനങ്ങളിൽ ലഗ്രാൻജിയൻ മാറില്ല.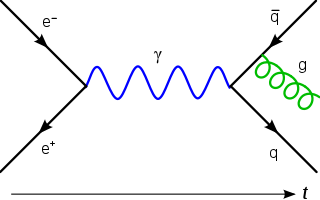
ഗണിത തമാശ: ഗണിതശാസ്ത്രത്തിന്റെ വശങ്ങളെ അല്ലെങ്കിൽ ഗണിതശാസ്ത്രജ്ഞരുടെ സ്റ്റീരിയോടൈപ്പിനെ ആശ്രയിക്കുന്ന ഒരു നർമ്മരൂപമാണ് ഗണിതശാസ്ത്ര തമാശ . നർമ്മം ഒരു ശബ്ദത്തിൽ നിന്നോ അല്ലെങ്കിൽ ഒരു ഗണിതശാസ്ത്ര പദത്തിന്റെ ഇരട്ട അർത്ഥത്തിൽ നിന്നോ അല്ലെങ്കിൽ ഒരു ഗണിതശാസ്ത്ര സങ്കൽപ്പത്തെക്കുറിച്ച് ഒരു സാധാരണക്കാരന്റെ തെറ്റിദ്ധാരണയിൽ നിന്നോ ഉണ്ടാകാം. ഗണിതശാസ്ത്രജ്ഞനും എഴുത്തുകാരനുമായ ജോൺ അലൻ പോളോസ് തന്റെ ഗണിതശാസ്ത്രവും നർമ്മവും എന്ന പുസ്തകത്തിൽ ഗണിതശാസ്ത്രത്തെ വരണ്ടതും formal പചാരികവുമായ ഒരു പ്രവർത്തനമായി കണക്കാക്കുന്നു, നർമ്മത്തിൽ ഓവർലാപ്പ് ചെയ്യുന്നു, അയഞ്ഞതും അപ്രസക്തവുമായ ഒരു പ്രവർത്തനം: ഇവ രണ്ടും "ബ play ദ്ധിക നാടകത്തിന്റെ" രൂപങ്ങളാണ്; രണ്ടിനും "യുക്തി, പാറ്റേൺ, നിയമങ്ങൾ, ഘടന" ഉണ്ട്; രണ്ടും "സാമ്പത്തികവും സ്പഷ്ടവുമാണ്".
അബെലിയൻ ഗ്രൂപ്പ്: ഗണിതശാസ്ത്രത്തിൽ, ഒരു ഗ്രൂപ്പ് ഗ്രൂപ്പിനെ ഒരു കമ്മ്യൂട്ടേറ്റീവ് ഗ്രൂപ്പ് എന്നും വിളിക്കുന്നു, അതിൽ ഗ്രൂപ്പ് പ്രവർത്തനം രണ്ട് ഗ്രൂപ്പ് ഘടകങ്ങളിൽ പ്രയോഗിക്കുന്നതിന്റെ ഫലം അവ എഴുതിയ ക്രമത്തെ ആശ്രയിക്കുന്നില്ല. അതായത്, ഗ്രൂപ്പ് പ്രവർത്തനം കമ്മ്യൂട്ടേറ്റീവ് ആണ്. ഒരു പ്രവർത്തനമെന്ന നിലയിൽ, പൂർണ്ണസംഖ്യകളും യഥാർത്ഥ സംഖ്യകളും അബെലിയൻ ഗ്രൂപ്പുകളായി മാറുന്നു, കൂടാതെ ഒരു ഹീലിയൻ ഗ്രൂപ്പിന്റെ ആശയം ഈ ഉദാഹരണങ്ങളുടെ പൊതുവൽക്കരണമായി കാണപ്പെടാം. പത്തൊൻപതാം നൂറ്റാണ്ടിന്റെ തുടക്കത്തിൽ ഗണിതശാസ്ത്രജ്ഞനായ നീൽസ് ഹെൻറിക് ആബെലിന്റെ പേരിലാണ് അബെലിയൻ ഗ്രൂപ്പുകൾക്ക് പേര് നൽകിയിരിക്കുന്നത്.
അബെലിയൻ ഗ്രൂപ്പ്: ഗണിതശാസ്ത്രത്തിൽ, ഒരു ഗ്രൂപ്പ് ഗ്രൂപ്പിനെ ഒരു കമ്മ്യൂട്ടേറ്റീവ് ഗ്രൂപ്പ് എന്നും വിളിക്കുന്നു, അതിൽ ഗ്രൂപ്പ് പ്രവർത്തനം രണ്ട് ഗ്രൂപ്പ് ഘടകങ്ങളിൽ പ്രയോഗിക്കുന്നതിന്റെ ഫലം അവ എഴുതിയ ക്രമത്തെ ആശ്രയിക്കുന്നില്ല. അതായത്, ഗ്രൂപ്പ് പ്രവർത്തനം കമ്മ്യൂട്ടേറ്റീവ് ആണ്. ഒരു പ്രവർത്തനമെന്ന നിലയിൽ, പൂർണ്ണസംഖ്യകളും യഥാർത്ഥ സംഖ്യകളും അബെലിയൻ ഗ്രൂപ്പുകളായി മാറുന്നു, കൂടാതെ ഒരു ഹീലിയൻ ഗ്രൂപ്പിന്റെ ആശയം ഈ ഉദാഹരണങ്ങളുടെ പൊതുവൽക്കരണമായി കാണപ്പെടാം. പത്തൊൻപതാം നൂറ്റാണ്ടിന്റെ തുടക്കത്തിൽ ഗണിതശാസ്ത്രജ്ഞനായ നീൽസ് ഹെൻറിക് ആബെലിന്റെ പേരിലാണ് അബെലിയൻ ഗ്രൂപ്പുകൾക്ക് പേര് നൽകിയിരിക്കുന്നത്.
അബെലിയൻ ഇന്റഗ്രൽ: ഗണിതശാസ്ത്രത്തിൽ, നോർവീജിയൻ ഗണിതശാസ്ത്രജ്ഞനായ നീൽസ് ഹെൻറിക് ആബെലിന്റെ പേരിലുള്ള ഒരു അബെലിയൻ ഇന്റഗ്രൽ , രൂപത്തിന്റെ സങ്കീർണ്ണ തലത്തിൽ ഒരു അവിഭാജ്യ ഘടകമാണ്
തുല്യമായ കോഹമോളജിക്ക് പ്രാദേശികവൽക്കരണ സൂത്രവാക്യം: ഡിഫറൻഷ്യൽ ജ്യാമിതിയിൽ, പ്രാദേശികവൽക്കരണ സൂത്രവാക്യം ഇപ്രകാരം പറയുന്നു: തുല്യമായി അടച്ച തുല്യമായ ഡിഫറൻഷ്യൽ ഫോമിനായി ടോറസ് പ്രവർത്തനം ഉപയോഗിച്ച് ഒര്ബിഫൊല്ദ് എം ന് ഒരു മതിയായ ചെറിയ വേണ്ടി ടി ടോറസിന്റെ ലീ ആൾജിബ്രയിൽ,
വ്യത്യസ്‌ത സീരീസ്: ഗണിതശാസ്ത്രത്തിൽ, വ്യത്യസ്‌ത ശ്രേണി എന്നത് സംയോജിതമല്ലാത്ത അനന്തമായ ഒരു ശ്രേണിയാണ്, അതായത് ശ്രേണിയുടെ ഭാഗിക സംഖ്യകളുടെ അനന്ത ശ്രേണിക്ക് പരിധിയില്ല.
മോണോയ്ഡ്: ഗണിതത്തിന്റെ ഒരു ശാഖയായ അമൂർത്ത ബീജഗണിതത്തിൽ, ഒരു മോണോയിഡ് എന്നത് ഒരു അനുബന്ധ ബൈനറി പ്രവർത്തനവും ഒരു ഐഡന്റിറ്റി ഘടകവും ഉൾക്കൊള്ളുന്ന ഒരു കൂട്ടമാണ്.
ക്ലാസ് ഫീൽഡ് സിദ്ധാന്തം: ഗണിതശാസ്ത്രത്തിൽ, ക്ലാസ് ഫീൽഡ് സിദ്ധാന്തം ബീജഗണിത സംഖ്യ സിദ്ധാന്തത്തിന്റെ ശാഖയാണ്, അത് നമ്പർ ഫീൽഡുകളുടെ വിപുലീകരണ വിപുലീകരണങ്ങൾ, പോസിറ്റീവ് സ്വഭാവമുള്ള ആഗോള ഫീൽഡുകൾ, പ്രാദേശിക ഫീൽഡുകൾ എന്നിവയുമായി ബന്ധപ്പെട്ടതാണ്. പതിനെട്ടാം നൂറ്റാണ്ടിന്റെ അവസാനത്തിൽ ഗാസ് നടത്തിയ ക്വാഡ്രാറ്റിക് പരസ്പര സഹകരണത്തിന്റെ തെളിവിലാണ് ഈ സിദ്ധാന്തത്തിന്റെ ഉത്ഭവം. ഈ ആശയങ്ങൾ അടുത്ത നൂറ്റാണ്ടിൽ വികസിപ്പിച്ചെടുത്തു, ഹിൽബെർട്ടിന്റെ ഒരു കൂട്ടം അനുമാനങ്ങൾക്ക് തുടക്കം കുറിച്ചു, പിന്നീട് തകഗിയും ആർട്ടിനും തെളിയിച്ചു. ഈ അനുമാനങ്ങളും അവയുടെ തെളിവുകളും ക്ലാസ് ഫീൽഡ് സിദ്ധാന്തത്തിന്റെ പ്രധാന ഘടകമാണ്.
ഐഡെംപോറ്റന്റ് (റിംഗ് തിയറി): മോതിരം സിദ്ധാന്തം ഒരു ഇദെംപൊതെംത് ഘടകം, അല്ലെങ്കിൽ ഒരു മോതിരം ഒരു ഇദെംപൊതെംത്, ഒരു അത്തരമൊരു 2 = ഒരു ഒരു മൂലകമാണ്. അതായത്, റിംഗിന്റെ ഗുണനത്തിന് കീഴിൽ മൂലകം ഐഡിയംപോട്ടന്റാണ്. ഇൻഡക്റ്റീവ് ആയി, ഏതെങ്കിലും പോസിറ്റീവ് സംഖ്യ n ന് a = a 2 = a 3 = a 4 = ... = a n എന്നും നിഗമനം ചെയ്യാം. ഉദാഹരണത്തിന്, ഒരു മാട്രിക്സ് റിങ്ങിന്റെ ഒരു ഐഡിയംപോട്ടന്റ് ഘടകം കൃത്യമായി ഒരു ഐഡിയംപോട്ടന്റ് മാട്രിക്സാണ്.
അബെലിയൻ സാൻഡ്‌പൈൽ മോഡൽ: സ്വയം സംഘടിത വിമർശനം പ്രദർശിപ്പിക്കുന്ന ചലനാത്മക സംവിധാനത്തിന്റെ ആദ്യത്തെ കണ്ടെത്തിയ ഉദാഹരണമാണ് അബെലിയൻ സാൻഡ്‌പൈൽ മോഡൽ , ബക്ക്-ടാങ്-വീസെൻഫെൽഡ് മോഡൽ എന്നും അറിയപ്പെടുന്നു. പെർ ബക്ക്, ചാവോ ടാങ്, കുർട്ട് വീസെൻ‌ഫെൽഡ് എന്നിവർ 1987 ൽ ഒരു പ്രബന്ധത്തിൽ ഇത് അവതരിപ്പിച്ചു.
അബെലിയൻ സാൻഡ്‌പൈൽ മോഡൽ: സ്വയം സംഘടിത വിമർശനം പ്രദർശിപ്പിക്കുന്ന ചലനാത്മക സംവിധാനത്തിന്റെ ആദ്യത്തെ കണ്ടെത്തിയ ഉദാഹരണമാണ് അബെലിയൻ സാൻഡ്‌പൈൽ മോഡൽ , ബക്ക്-ടാങ്-വീസെൻഫെൽഡ് മോഡൽ എന്നും അറിയപ്പെടുന്നു. പെർ ബക്ക്, ചാവോ ടാങ്, കുർട്ട് വീസെൻ‌ഫെൽഡ് എന്നിവർ 1987 ൽ ഒരു പ്രബന്ധത്തിൽ ഇത് അവതരിപ്പിച്ചു.
അബെലിയൻ ഇനം: ഗണിതശാസ്ത്രത്തിൽ, പ്രത്യേകിച്ച് ബീജീയജ്യാമിതി, സങ്കീർണ്ണമായ വിശകലനം ബീജീയ എണ്ണം തിയറി, ഒരു ക്രമഗ്രൂപ്പ് മുറികൾ ഒരു ബീജീയ ഗ്രൂപ്പ് ഒരു പ്രൊജെച്തിവെ ബീജീയ വൈവിധ്യം, അതായത്, പതിവ് പ്രവർത്തനങ്ങൾ തിരിക്കാം കഴിയുന്ന ഒരു ഗ്രൂപ്പ് നിയമം ഉണ്ട്. ബീജഗണിത ജ്യാമിതിയിലും ബീജഗണിത ജ്യാമിതിയിലും സംഖ്യ സിദ്ധാന്തത്തിലും മറ്റ് വിഷയങ്ങളെക്കുറിച്ചുള്ള കൂടുതൽ ഗവേഷണങ്ങൾക്ക് ഒഴിച്ചുകൂടാനാവാത്ത ഉപകരണങ്ങളിൽ അബെലിയൻ ഇനങ്ങൾ ഒരേ സമയം ഉൾപ്പെടുന്നു.
സെമിഗ്രൂപ്പ്: ഗണിതശാസ്ത്രത്തിൽ, ഒരു സെമിഗ്രൂപ്പ് ഒരു ബീജഗണിത ഘടനയാണ്, ഒരു കൂട്ടം ഒരു അനുബന്ധ ബൈനറി പ്രവർത്തനവും ഉൾക്കൊള്ളുന്നു.
മൊഡ്യൂളുകളുടെ കറ്റ: ഗണിതശാസ്ത്രത്തിൽ ഒ ഒരു കറ്റ -മൊദുലെസ് അല്ലെങ്കിൽ ഒരു വലയത്തോടു സ്പേസ് മേൽ ഒരു ഒ -മൊദുലെ ഒരു കറ്റ എഫ് ഇത്തരം, ഏതെങ്കിലും തുറന്ന ഉപസെറ്റ് എക്സ് യു വേണ്ടി, എഫ് (യു) ഒരു ഹേ (യു) -മൊദുലെ ആൻഡ് നിയന്ത്രണം മാപ്പുകൾ ആണ് എഫ് (യു) → എഫ് (വി) നിയന്ത്രണം കിടപിടിക്കുന്നതാണ് മാപ്പുകൾ ഹേ (യു) → ഹേ (വി): എഫ്എസ് നിയന്ത്രണം ഹേ ഏതെങ്കിലും എഫ് വേണ്ടി ങ്ങൾ (യു) എഫ് തവണ നിയന്ത്രണം ആണ് എഫ് ല് ( യു ).
അബെലിയൻ ഗ്രൂപ്പ്: ഗണിതശാസ്ത്രത്തിൽ, ഒരു ഗ്രൂപ്പ് ഗ്രൂപ്പിനെ ഒരു കമ്മ്യൂട്ടേറ്റീവ് ഗ്രൂപ്പ് എന്നും വിളിക്കുന്നു, അതിൽ ഗ്രൂപ്പ് പ്രവർത്തനം രണ്ട് ഗ്രൂപ്പ് ഘടകങ്ങളിൽ പ്രയോഗിക്കുന്നതിന്റെ ഫലം അവ എഴുതിയ ക്രമത്തെ ആശ്രയിക്കുന്നില്ല. അതായത്, ഗ്രൂപ്പ് പ്രവർത്തനം കമ്മ്യൂട്ടേറ്റീവ് ആണ്. ഒരു പ്രവർത്തനമെന്ന നിലയിൽ, പൂർണ്ണസംഖ്യകളും യഥാർത്ഥ സംഖ്യകളും അബെലിയൻ ഗ്രൂപ്പുകളായി മാറുന്നു, കൂടാതെ ഒരു ഹീലിയൻ ഗ്രൂപ്പിന്റെ ആശയം ഈ ഉദാഹരണങ്ങളുടെ പൊതുവൽക്കരണമായി കാണപ്പെടാം. പത്തൊൻപതാം നൂറ്റാണ്ടിന്റെ തുടക്കത്തിൽ ഗണിതശാസ്ത്രജ്ഞനായ നീൽസ് ഹെൻറിക് ആബെലിന്റെ പേരിലാണ് അബെലിയൻ ഗ്രൂപ്പുകൾക്ക് പേര് നൽകിയിരിക്കുന്നത്.
ഹാബെലിന്റെ സിദ്ധാന്തം: ഗണിതശാസ്ത്രത്തിൽ, പവർ സീരീസിനായുള്ള ആബെലിന്റെ സിദ്ധാന്തം ഒരു പവർ സീരീസിന്റെ പരിധിയെ അതിന്റെ ഗുണകങ്ങളുടെ ആകെത്തുകയുമായി ബന്ധിപ്പിക്കുന്നു. നോർവീജിയൻ ഗണിതശാസ്ത്രജ്ഞൻ നീൽസ് ഹെൻറിക് ആബെലിന്റെ പേരിലാണ് ഇതിന് പേര് നൽകിയിരിക്കുന്നത്.
അബെലിയൻ ഉപരിതലം: ഗണിതശാസ്ത്രത്തിൽ, ഒരു അബെലിയൻ ഉപരിതലം 2-ഡൈമൻഷണൽ അബെലിയൻ ഇനമാണ്.
അബെലിയൻ, ട ub ബെറിയൻ സിദ്ധാന്തങ്ങൾ: ഗണിതശാസ്ത്രത്തിൽ, ഒരേ ശ്രേണി നൽകുന്നതിന് വ്യത്യസ്ത ശ്രേണികളെ സംഗ്രഹിക്കുന്നതിനുള്ള രണ്ട് രീതികൾക്ക് വ്യവസ്ഥകൾ നൽകുന്ന സിദ്ധാന്തങ്ങളാണ് അബെലിയൻ, ട ub ബെറിയൻ സിദ്ധാന്തങ്ങൾ , നീൽസ് ഹെൻറിക് ആബെലിന്റെയും ആൽഫ്രഡ് ട ub ബറിന്റെയും പേരിലാണ് ഇത് അറിയപ്പെടുന്നത്. ഒരു ശ്രേണി ചില പരിധികളിലേക്ക് ഒത്തുചേരുന്നുവെങ്കിൽ അതിന്റെ ആബെൽ തുക ഒരേ പരിധിയാണെന്ന് കാണിക്കുന്ന ഹാബെലിന്റെ സിദ്ധാന്തമാണ് യഥാർത്ഥ ഉദാഹരണങ്ങൾ, ഒരു ശ്രേണിയുടെ ആബെൽ തുക നിലവിലുണ്ടെങ്കിൽ ഗുണകങ്ങൾ പര്യാപ്തമാണെങ്കിൽ സീരീസ് ആബെലിലേക്ക് സംയോജിക്കുന്നു തുക. കൂടുതൽ പൊതുവായ സംഗ്രഹ രീതികൾക്ക് കൂടുതൽ പൊതുവായ അബെലിയൻ, ട ub ബേറിയൻ സിദ്ധാന്തങ്ങൾ സമാന ഫലങ്ങൾ നൽകുന്നു.
അബെലിയൻ ഇനം: ഗണിതശാസ്ത്രത്തിൽ, പ്രത്യേകിച്ച് ബീജീയജ്യാമിതി, സങ്കീർണ്ണമായ വിശകലനം ബീജീയ എണ്ണം തിയറി, ഒരു ക്രമഗ്രൂപ്പ് മുറികൾ ഒരു ബീജീയ ഗ്രൂപ്പ് ഒരു പ്രൊജെച്തിവെ ബീജീയ വൈവിധ്യം, അതായത്, പതിവ് പ്രവർത്തനങ്ങൾ തിരിക്കാം കഴിയുന്ന ഒരു ഗ്രൂപ്പ് നിയമം ഉണ്ട്. ബീജഗണിത ജ്യാമിതിയിലും ബീജഗണിത ജ്യാമിതിയിലും സംഖ്യ സിദ്ധാന്തത്തിലും മറ്റ് വിഷയങ്ങളെക്കുറിച്ചുള്ള കൂടുതൽ ഗവേഷണങ്ങൾക്ക് ഒഴിച്ചുകൂടാനാവാത്ത ഉപകരണങ്ങളിൽ അബെലിയൻ ഇനങ്ങൾ ഒരേ സമയം ഉൾപ്പെടുന്നു.
അബെലിയൻ ഇനം: ഗണിതശാസ്ത്രത്തിൽ, പ്രത്യേകിച്ച് ബീജീയജ്യാമിതി, സങ്കീർണ്ണമായ വിശകലനം ബീജീയ എണ്ണം തിയറി, ഒരു ക്രമഗ്രൂപ്പ് മുറികൾ ഒരു ബീജീയ ഗ്രൂപ്പ് ഒരു പ്രൊജെച്തിവെ ബീജീയ വൈവിധ്യം, അതായത്, പതിവ് പ്രവർത്തനങ്ങൾ തിരിക്കാം കഴിയുന്ന ഒരു ഗ്രൂപ്പ് നിയമം ഉണ്ട്. ബീജഗണിത ജ്യാമിതിയിലും ബീജഗണിത ജ്യാമിതിയിലും സംഖ്യ സിദ്ധാന്തത്തിലും മറ്റ് വിഷയങ്ങളെക്കുറിച്ചുള്ള കൂടുതൽ ഗവേഷണങ്ങൾക്ക് ഒഴിച്ചുകൂടാനാവാത്ത ഉപകരണങ്ങളിൽ അബെലിയൻ ഇനങ്ങൾ ഒരേ സമയം ഉൾപ്പെടുന്നു.
ഒരു വിഭാഗത്തിന്റെ പ്രാദേശികവൽക്കരണം: ഗണിതശാസ്ത്രത്തിൽ, ഒരു വിഭാഗത്തിന്റെ പ്രാദേശികവൽക്കരണം ചില മോർഫിസങ്ങളുടെ ശേഖരണത്തിനായി ഒരു വിഭാഗത്തിൽ വിപരീത മോർഫിസങ്ങൾ ചേർത്ത് അവയെ ഐസോമോണിസങ്ങളായി പരിമിതപ്പെടുത്തുന്നു. ഇത് ring ദ്യോഗികമായി ഒരു മോതിരം പ്രാദേശികവൽക്കരിക്കുന്ന പ്രക്രിയയ്ക്ക് സമാനമാണ്; ഇത് പൊതുവെ മുമ്പ് ഇല്ലാത്ത വസ്തുക്കളെ ഐസോമോഫിക് ആക്കുന്നു. ഹോമോടോപ്പി സിദ്ധാന്തത്തിൽ, ഉദാഹരണത്തിന്, ഹോമോടോപ്പി വരെ വിപരീതമായി മാപ്പിംഗിന് ധാരാളം ഉദാഹരണങ്ങളുണ്ട്; അതിനാൽ ഹോമോടോപ്പിക്ക് തുല്യമായ ഇടങ്ങളുടെ വലിയ ക്ലാസുകൾ. പ്രാദേശികവൽക്കരിച്ച വിഭാഗത്തിൽ പ്രവർത്തിക്കുന്നതിനുള്ള മറ്റൊരു പേരാണ് ഭിന്നസംഖ്യകളുടെ കാൽക്കുലസ് .
അബെലിയൻ ഇനം: ഗണിതശാസ്ത്രത്തിൽ, പ്രത്യേകിച്ച് ബീജീയജ്യാമിതി, സങ്കീർണ്ണമായ വിശകലനം ബീജീയ എണ്ണം തിയറി, ഒരു ക്രമഗ്രൂപ്പ് മുറികൾ ഒരു ബീജീയ ഗ്രൂപ്പ് ഒരു പ്രൊജെച്തിവെ ബീജീയ വൈവിധ്യം, അതായത്, പതിവ് പ്രവർത്തനങ്ങൾ തിരിക്കാം കഴിയുന്ന ഒരു ഗ്രൂപ്പ് നിയമം ഉണ്ട്. ബീജഗണിത ജ്യാമിതിയിലും ബീജഗണിത ജ്യാമിതിയിലും സംഖ്യ സിദ്ധാന്തത്തിലും മറ്റ് വിഷയങ്ങളെക്കുറിച്ചുള്ള കൂടുതൽ ഗവേഷണങ്ങൾക്ക് ഒഴിച്ചുകൂടാനാവാത്ത ഉപകരണങ്ങളിൽ അബെലിയൻ ഇനങ്ങൾ ഒരേ സമയം ഉൾപ്പെടുന്നു.
അബെലിയൻ ഇനങ്ങളുടെ സങ്കീർണ്ണ ഗുണനം: ഗണിതശാസ്ത്രത്തിൽ ഒരു ക്രമഗ്രൂപ്പ് മുറികൾ ഒരു കെ അതിന്റെ എംദൊമൊര്ഫിസ്മ് റിങ് അവസാനം (എ) ഒരു വലിയ മതി ചൊംമുതതിവെ സുബ്രിന്ഗ് ഉണ്ടെങ്കിൽ മുഖ്യമന്ത്രി-തരം പറയപ്പെടുന്നു ഫീൽഡ് നിർവചിച്ചിരിക്കുന്നത്. പത്തൊൻപതാം നൂറ്റാണ്ടിൽ എലിപ്റ്റിക് കർവുകൾക്കായി വികസിപ്പിച്ച സങ്കീർണ്ണമായ ഗുണന സിദ്ധാന്തത്തിൽ നിന്നാണ് ഇവിടെയുള്ള പദങ്ങൾ. ഇരുപതാം നൂറ്റാണ്ടിലെ ബീജഗണിത സംഖ്യ സിദ്ധാന്തത്തിലും ബീജഗണിത ജ്യാമിതിയിലുമുള്ള ഒരു പ്രധാന നേട്ടം, അബെലിയൻ വൈവിധ്യമാർന്ന അളവുകൾക്കായുള്ള അനുബന്ധ സിദ്ധാന്തത്തിന്റെ ശരിയായ ഫോർമുലേഷനുകൾ കണ്ടെത്തുക എന്നതാണ് d > 1. പ്രശ്നം ആഴത്തിലുള്ള അമൂർത്ത തലത്തിലാണ്, കാരണം ഇത് വളരെ കഠിനമാണ് നിരവധി സങ്കീർണ്ണ വേരിയബിളുകളുടെ വിശകലന പ്രവർത്തനങ്ങൾ കൈകാര്യം ചെയ്യുന്നതിന്.
അബെലിയൻ വോൺ ന്യൂമാൻ ബീജഗണിതം: ഫങ്ഷണൽ വിശകലനത്തിൽ, ഒരു ക്രമഗ്രൂപ്പ് വോൺ ന്യൂമാൻ ബീജഗണിതം ഒരു ഓഫിട്ടു സ്പേസ് ന് ഓപ്പറേറ്റേഴ്സ് ഘടകങ്ങൾ യാത്ര അതിൽ ഒരു വോൺ ന്യൂമാൻ ബീജഗണിതം ആണ്.
അബെലിയൻ വോൺ ന്യൂമാൻ ബീജഗണിതം: ഫങ്ഷണൽ വിശകലനത്തിൽ, ഒരു ക്രമഗ്രൂപ്പ് വോൺ ന്യൂമാൻ ബീജഗണിതം ഒരു ഓഫിട്ടു സ്പേസ് ന് ഓപ്പറേറ്റേഴ്സ് ഘടകങ്ങൾ യാത്ര അതിൽ ഒരു വോൺ ന്യൂമാൻ ബീജഗണിതം ആണ്.
കമ്മ്യൂട്ടേറ്റർ ഉപഗ്രൂപ്പ്: ഗണിതശാസ്ത്രത്തിൽ, കൂടുതൽ വ്യക്തമായി അമൂർത്ത ബീജഗണിതത്തിൽ, ഗ്രൂപ്പിലെ എല്ലാ കമ്മ്യൂട്ടേറ്റർമാരും സൃഷ്ടിക്കുന്ന ഉപഗ്രൂപ്പാണ് കമ്മ്യൂട്ടേറ്റർ ഉപഗ്രൂപ്പ് അല്ലെങ്കിൽ ഒരു ഗ്രൂപ്പിന്റെ ഉരുത്തിരിഞ്ഞ ഉപഗ്രൂപ്പ് .
കമ്മ്യൂട്ടേറ്റർ ഉപഗ്രൂപ്പ്: ഗണിതശാസ്ത്രത്തിൽ, കൂടുതൽ വ്യക്തമായി അമൂർത്ത ബീജഗണിതത്തിൽ, ഗ്രൂപ്പിലെ എല്ലാ കമ്മ്യൂട്ടേറ്റർമാരും സൃഷ്ടിക്കുന്ന ഉപഗ്രൂപ്പാണ് കമ്മ്യൂട്ടേറ്റർ ഉപഗ്രൂപ്പ് അല്ലെങ്കിൽ ഒരു ഗ്രൂപ്പിന്റെ ഉരുത്തിരിഞ്ഞ ഉപഗ്രൂപ്പ് .
ഹാബെലിയൻസ്: നാലാം നൂറ്റാണ്ടിൽ ആർക്കേഡിയസിന്റെ ഭരണകാലത്ത് വടക്കേ ആഫ്രിക്കയിലെ ഹിപ്പോ റീജിയസിനടുത്തുള്ള നാട്ടിൻപുറങ്ങളിൽ വ്യാപിച്ച ഒരു ക്രിസ്ത്യൻ വിഭാഗമായിരുന്നു അബെലിയക്കാർ . അവർ ഹാബെലിനെപ്പോലെ സ്ഥിരമായി ജീവിച്ചു. അവർ വിവാഹിതരാകണമെന്ന് ആവശ്യപ്പെട്ടിരുന്നുവെങ്കിലും വിവാഹം പൂർത്തിയാക്കാൻ വിലക്കി. ഓരോ ദമ്പതികൾക്കും രണ്ട് കുട്ടികളെയും ഒരു ആൺകുട്ടിയെയും പെൺകുട്ടിയെയും ദത്തെടുക്കേണ്ടതുണ്ടായിരുന്നു. വളർത്തു മാതാപിതാക്കൾ മരിച്ചപ്പോൾ, ഈ ദത്തെടുക്കുന്നവർ പിന്നീട് ഒരു ദമ്പതികളെ രൂപീകരിച്ച് രണ്ട് കുട്ടികളെ ദത്തെടുക്കും. ഹാബേലിന്റെ മക്കളെയൊന്നും വേദഗ്രന്ഥത്തിൽ പരാമർശിച്ചിട്ടില്ലാത്തതിനാൽ, അവനില്ലെന്ന് ഹാബിലിയക്കാർ കരുതി. ഈ കാഴ്ചപ്പാടിനെ യഹൂദരും മനിചീൻ പ്രചോദനം ഉൾക്കൊണ്ട ഹാബെസ്റ്റിക് വീക്ഷണങ്ങളും സ്വാധീനിച്ചു, അദ്ദേഹം വിവാഹിതനായിരിക്കുമ്പോൾ തന്നെ കന്യകയായി തുടർന്നു. ഈ വിഭാഗത്തിന്റെ ഏക രേഖ ഹിപ്പോയുടെ ഡി ഹെറെറ്റിസിസ് സിഎച്ചിലെ അഗസ്റ്റിൻ ആണ് . 87 , ഇവിടെ അദ്ദേഹം എഴുതുന്നത് ഈ വിഭാഗത്തിന്റെ പേര് പ്യൂണിക് ഉത്ഭവം ആയിരിക്കാം. അഗസ്റ്റിൻ പറയുന്നതനുസരിച്ച്, 428-ൽ അതിന്റെ അവസാന അംഗങ്ങൾ കത്തോലിക്കാ മതത്തിലേക്ക് മാറിയപ്പോൾ ഈ വിഭാഗം വംശനാശം സംഭവിച്ചു.
അബെലിച്നസ്: കാൻഡെലറോസ് രൂപവത്കരണത്തിൽ നിന്നും റിയോ ലിമെയ് രൂപീകരണത്തിൽ നിന്നും ദിനോസർ കാൽപ്പാടുകളുടെ വംശനാശം സംഭവിച്ച ഇക്നോജെനസാണ് അബെലിച്നസ് . അർജന്റീനയിൽ ആദ്യമായി കണ്ടെത്തിയ ഇക്നോസ്പെസിസ് തരം, അബെലിച്നസ് അസ്റ്റിഗെറ , ഇതുവരെ കണ്ടെത്തിയതിൽ വച്ച് ഏറ്റവും വലിയ ദിനോസർ കാൽപ്പാടായി ഇത് രേഖപ്പെടുത്തി. 12.5-13 മീറ്റർ നീളത്തിൽ അബെലിച്നസ് വളർന്നു.
അബെലിൻ: അബെലിൻ ഒരു കുടുംബപ്പേരാണ്, ഇത് ഇനിപ്പറയുന്നവ പരാമർശിക്കാം: ജീൻ പിയറി ആബെലിൻ, ഫ്രഞ്ച് രാഷ്ട്രീയക്കാരൻ ജോഹാൻ ഫിലിപ്പ് അബെലിൻ, ജർമ്മൻ ചരിത്രകാരൻ സ്വിസ് മന o ശാസ്ത്രവിദഗ്ദ്ധനും ആദ്യകാല ത്രികോണ സിദ്ധാന്തത്തിന്റെ സ്ഥാപകനുമായ ഏണസ്റ്റ് ആബെലിൻ
ജീൻ പിയറി ആബെലിൻ: ജീൻ പിയറി ആബെലിൻ ഒരു ഫ്രഞ്ച് രാഷ്ട്രീയക്കാരനാണ്.
അബെലിൻ പ്രതികരണം: അബെലിന് പ്രതികരണം രക്തവും മൂത്രത്തിൽ അര്സ്ഫെനമിനെ ആൻഡ് നെഒഅര്സ്ഫെനമിനെ സാന്നിധ്യം തെളിയിച്ചു ഒരു ഗുണപരമായ പ്രതികരണം ആണ്.
അബെലിന്റെ വീട്: ഡാനിഷ് വെസ്റ്റ് കോസ്റ്റിലെ റിങ്‌കോബിംഗ്-സ്കജെർൻ മുനിസിപ്പാലിറ്റിയുടെ എച്ച്വിഡ് സാൻഡെയുടെ തെക്ക് ഭാഗത്തുള്ള ഹ ur ർവിഗിലെ ഒരു മുൻ വാട്ടർഫ്രണ്ട് ഫാം ഹ house സാണ് അബെലിൻ ഹ House സ്. 1970 കളിൽ ഇത് ഹോംസ്‌ലാൻഡ് ഡ്യൂൺസിനായി ഒരു പ്രാദേശിക ചരിത്ര മ്യൂസിയമാക്കി മാറ്റി, ഇപ്പോൾ റിംഗ്‌കോബിംഗ്-സ്കജർൻ മ്യൂസിയത്തിന്റെ ഭാഗമാണ്.
അബിലീൻ, കൻസാസ്: അമേരിക്കൻ ഐക്യനാടുകളിലെ കൻസാസിലെ ഡിക്കിൻസൺ കൗണ്ടിയിലെ ഒരു നഗരവും ക seat ണ്ടി സീറ്റുമാണ് അബിലീൻ . 2010 ലെ സെൻസസ് പ്രകാരം നഗര ജനസംഖ്യ 6,844 ആയിരുന്നു. ഡ്വൈറ്റ് ഡി. ഐസൻ‌ഹോവർ പ്രസിഡൻഷ്യൽ ലൈബ്രറിയും മ്യൂസിയവും അബിലൈനിലാണ്. ഗ്രേഹ ound ണ്ട് ഹാൾ ഓഫ് ഫെയിമിന്റെ ആസ്ഥാനം കൂടിയാണ് അബിലീൻ.
അബിലീൻ, ടെക്സസ്: അമേരിക്കൻ ഐക്യനാടുകളിലെ ടെക്സസിലെ ടെയ്‌ലർ, ജോൺസ് കൗണ്ടികളിലെ ഒരു നഗരമാണ് അബിലീൻ . 2010 ലെ സെൻസസ് പ്രകാരം ജനസംഖ്യ 117,063 ആയിരുന്നു, ഇത് ടെക്സസ് സംസ്ഥാനത്തെ ഏറ്റവും ജനസംഖ്യയുള്ള 27-ാമത്തെ നഗരമായി മാറി. 2017 ൽ 170,219 ജനസംഖ്യയുള്ള അബിലീൻ മെട്രോപൊളിറ്റൻ സ്റ്റാറ്റിസ്റ്റിക്കൽ ഏരിയയുടെ പ്രധാന നഗരമാണിത്. ടെയ്‌ലർ കൗണ്ടിയിലെ കൗണ്ടി സീറ്റാണിത്. നഗരത്തിന്റെ പടിഞ്ഞാറ് ഭാഗത്താണ് ഡൈസ് എയർഫോഴ്സ് ബേസ് സ്ഥിതി ചെയ്യുന്നത്.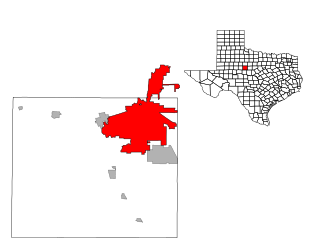
അബിലീൻ, ടെക്സസ്: അമേരിക്കൻ ഐക്യനാടുകളിലെ ടെക്സസിലെ ടെയ്‌ലർ, ജോൺസ് കൗണ്ടികളിലെ ഒരു നഗരമാണ് അബിലീൻ . 2010 ലെ സെൻസസ് പ്രകാരം ജനസംഖ്യ 117,063 ആയിരുന്നു, ഇത് ടെക്സസ് സംസ്ഥാനത്തെ ഏറ്റവും ജനസംഖ്യയുള്ള 27-ാമത്തെ നഗരമായി മാറി. 2017 ൽ 170,219 ജനസംഖ്യയുള്ള അബിലീൻ മെട്രോപൊളിറ്റൻ സ്റ്റാറ്റിസ്റ്റിക്കൽ ഏരിയയുടെ പ്രധാന നഗരമാണിത്. ടെയ്‌ലർ കൗണ്ടിയിലെ കൗണ്ടി സീറ്റാണിത്. നഗരത്തിന്റെ പടിഞ്ഞാറ് ഭാഗത്താണ് ഡൈസ് എയർഫോഴ്സ് ബേസ് സ്ഥിതി ചെയ്യുന്നത്.
ഡൈസ് എയർഫോഴ്സ് ബേസ്: ടെക്സസിലെ അബിലീനിന് ഏകദേശം 7 മൈൽ (11 കിലോമീറ്റർ) തെക്ക് പടിഞ്ഞാറായി സ്ഥിതിചെയ്യുന്ന യുണൈറ്റഡ് സ്റ്റേറ്റ്സ് വ്യോമസേനാ താവളമാണ് ഡൈസ് എയർഫോഴ്സ് ബേസ് (എ എഫ് ബി) .
ഡൈസ് എയർഫോഴ്സ് ബേസ്: ടെക്സസിലെ അബിലീനിന് ഏകദേശം 7 മൈൽ (11 കിലോമീറ്റർ) തെക്ക് പടിഞ്ഞാറായി സ്ഥിതിചെയ്യുന്ന യുണൈറ്റഡ് സ്റ്റേറ്റ്സ് വ്യോമസേനാ താവളമാണ് ഡൈസ് എയർഫോഴ്സ് ബേസ് (എ എഫ് ബി) .
ഡൈസ് എയർഫോഴ്സ് ബേസ്: ടെക്സസിലെ അബിലീനിന് ഏകദേശം 7 മൈൽ (11 കിലോമീറ്റർ) തെക്ക് പടിഞ്ഞാറായി സ്ഥിതിചെയ്യുന്ന യുണൈറ്റഡ് സ്റ്റേറ്റ്സ് വ്യോമസേനാ താവളമാണ് ഡൈസ് എയർഫോഴ്സ് ബേസ് (എ എഫ് ബി) .
അബെലിനോ മാനുവൽ അപ്പീലിയോ: ചിലിയൻ ആംഗ്ലിക്കൻ ബിഷപ്പാണ് അബെലിനോ മാനുവൽ അപ്പീലിയോ : മുമ്പ് അറൗകാനിയയിലെ സഹായ ബിഷപ്പായിരുന്നു, 2018 മുതൽ ചിലിയിലെ 40-ാമത്തെയും ഏറ്റവും പുതിയ പ്രവിശ്യയായ ടെമുക്കോ ബിഷപ്പായിരുന്നു.
അബെല്ലിയോ: ഗാലിയ അക്വിറ്റാനിയയിലെ ഗാരോൺ താഴ്‌വരയിൽ ആരാധിക്കപ്പെട്ടിരുന്ന ഒരു ദൈവമായിരുന്നു അബെല്ലിയോ , പ്രധാനമായും പൈറീനീസിലെ കമ്മിംഗസിൽ നിന്ന് കണ്ടെത്തിയ നിരവധി ലിഖിതങ്ങളാൽ ഇത് അറിയപ്പെടുന്നു. അദ്ദേഹം ആപ്പിൾ മരങ്ങളുടെയോ സൂര്യന്റെയോ ദേവനായിരിക്കാം.
ചാസ്സെലാസ്: പ്രധാനമായും സ്വിറ്റ്സർലൻഡ്, ഫ്രാൻസ്, ജർമ്മനി, പോർച്ചുഗൽ, ഹംഗറി, റൊമാനിയ, ന്യൂസിലാന്റ്, ചിലി എന്നിവിടങ്ങളിൽ വളർത്തുന്ന ഒരു വൈൻ മുന്തിരി ഇനമാണ് ചാസെലാസ് അല്ലെങ്കിൽ ചാസ്സെലാസ് ബ്ലാങ്ക് . പൂർണ്ണവും വരണ്ടതും ഫലപ്രദവുമായ വെളുത്ത വീഞ്ഞാണ് ചാസെലാസ്. തുർക്കിയിലും ഹംഗറിയിലും വ്യാപകമായി വളരുന്ന ഒരു മേശ മുന്തിരിപ്പഴം എന്ന നിലയിലും ഇത് അനുയോജ്യമാണ്.