Abstract Emotions, Abstract Emotions, Abstract Entity

അമൂർത്ത വികാരങ്ങൾ: അമേരിക്കൻ ജാസ്, ആർ & ബി ഗായിക വെറോണിക്ക "റാണ്ടി" ക്രോഫോർഡ് എന്നിവരുടെ എട്ടാമത്തെ സ്റ്റുഡിയോ ആൽബമാണ് അമൂർത്ത വികാരങ്ങൾ . യുഎസ് ആൽബങ്ങളുടെ ചാർട്ടിൽ ഇത് 178 ആം സ്ഥാനത്തും യുഎസ് ആർ & ബി ചാർട്ടിൽ 53 ആം സ്ഥാനത്തും യുകെ ആൽബങ്ങളുടെ ചാർട്ടിൽ 14 ആം സ്ഥാനത്തും എത്തി. നൈറ്റ്ലൈൻ ആൽബത്തിനൊപ്പം 2013 ഒക്ടോബർ 14 ന് ഇത് സിഡിയിൽ നൽകി.
അമൂർത്ത വികാരങ്ങൾ: അമേരിക്കൻ ജാസ്, ആർ & ബി ഗായിക വെറോണിക്ക "റാണ്ടി" ക്രോഫോർഡ് എന്നിവരുടെ എട്ടാമത്തെ സ്റ്റുഡിയോ ആൽബമാണ് അമൂർത്ത വികാരങ്ങൾ . യുഎസ് ആൽബങ്ങളുടെ ചാർട്ടിൽ ഇത് 178 ആം സ്ഥാനത്തും യുഎസ് ആർ & ബി ചാർട്ടിൽ 53 ആം സ്ഥാനത്തും യുകെ ആൽബങ്ങളുടെ ചാർട്ടിൽ 14 ആം സ്ഥാനത്തും എത്തി. നൈറ്റ്ലൈൻ ആൽബത്തിനൊപ്പം 2013 ഒക്ടോബർ 14 ന് ഇത് സിഡിയിൽ നൽകി.
അമൂർത്ത എന്റിറ്റി: ഫിന്നിഷ് മെലോഡിക് ഡെത്ത് മെറ്റൽ ബാൻഡ് കിയാനയുടെ ആദ്യ ആൽബമാണ് അബ്‌സ്ട്രാക്റ്റ് എന്റിറ്റി .
അമൂർത്ത എന്റിറ്റി: ഫിന്നിഷ് മെലോഡിക് ഡെത്ത് മെറ്റൽ ബാൻഡ് കിയാനയുടെ ആദ്യ ആൽബമാണ് അബ്‌സ്ട്രാക്റ്റ് എന്റിറ്റി .
അമൂർത്ത പദപ്രയോഗം: 1940 കളിൽ ന്യൂയോർക്കിൽ വികസിപ്പിച്ച അമേരിക്കൻ പെയിന്റിംഗിലെ രണ്ടാം ലോക മഹായുദ്ധാനന്തര കലാ പ്രസ്ഥാനമാണ് അമൂർത്ത എക്സ്പ്രഷനിസം . അന്താരാഷ്ട്ര സ്വാധീനം നേടുകയും ന്യൂയോർക്ക് നഗരത്തെ പാശ്ചാത്യ കലാ ലോകത്തിന്റെ കേന്ദ്രത്തിൽ ഉൾപ്പെടുത്തുകയും ചെയ്ത ആദ്യത്തെ അമേരിക്കൻ പ്രസ്ഥാനമാണിത്. മുമ്പ് പാരീസ് നിറച്ച ഈ പങ്ക്. "അമൂർത്ത എക്സ്പ്രഷനിസം" എന്ന പദം അമേരിക്കൻ കലയിൽ ആദ്യമായി കലാ നിരൂപകനായ റോബർട്ട് കോട്ട്സ് പ്രയോഗിച്ചെങ്കിലും, ജർമ്മൻ എക്സ്പ്രഷനിസത്തെക്കുറിച്ച് 1919 ൽ ജർമ്മനിയിൽ ആദ്യമായി ഡെർ സ്റ്റർം മാസികയിൽ ഇത് ഉപയോഗിച്ചു. അമേരിക്കൻ ഐക്യനാടുകളിൽ, വാസിലി കാൻഡിൻസ്കിയുടെ കൃതികളുമായി ബന്ധപ്പെട്ട് 1929 ൽ ആദ്യമായി ഈ പദം ഉപയോഗിച്ചതാണ് ആൽഫ്രഡ് ബാർ.
അമൂർത്ത പദപ്രയോഗം: 1940 കളിൽ ന്യൂയോർക്കിൽ വികസിപ്പിച്ച അമേരിക്കൻ പെയിന്റിംഗിലെ രണ്ടാം ലോക മഹായുദ്ധാനന്തര കലാ പ്രസ്ഥാനമാണ് അമൂർത്ത എക്സ്പ്രഷനിസം . അന്താരാഷ്ട്ര സ്വാധീനം നേടുകയും ന്യൂയോർക്ക് നഗരത്തെ പാശ്ചാത്യ കലാ ലോകത്തിന്റെ കേന്ദ്രത്തിൽ ഉൾപ്പെടുത്തുകയും ചെയ്ത ആദ്യത്തെ അമേരിക്കൻ പ്രസ്ഥാനമാണിത്. മുമ്പ് പാരീസ് നിറച്ച ഈ പങ്ക്. "അമൂർത്ത എക്സ്പ്രഷനിസം" എന്ന പദം അമേരിക്കൻ കലയിൽ ആദ്യമായി കലാ നിരൂപകനായ റോബർട്ട് കോട്ട്സ് പ്രയോഗിച്ചെങ്കിലും, ജർമ്മൻ എക്സ്പ്രഷനിസത്തെക്കുറിച്ച് 1919 ൽ ജർമ്മനിയിൽ ആദ്യമായി ഡെർ സ്റ്റർം മാസികയിൽ ഇത് ഉപയോഗിച്ചു. അമേരിക്കൻ ഐക്യനാടുകളിൽ, വാസിലി കാൻഡിൻസ്കിയുടെ കൃതികളുമായി ബന്ധപ്പെട്ട് 1929 ൽ ആദ്യമായി ഈ പദം ഉപയോഗിച്ചതാണ് ആൽഫ്രഡ് ബാർ.
അമൂർത്ത പദപ്രയോഗം: 1940 കളിൽ ന്യൂയോർക്കിൽ വികസിപ്പിച്ച അമേരിക്കൻ പെയിന്റിംഗിലെ രണ്ടാം ലോക മഹായുദ്ധാനന്തര കലാ പ്രസ്ഥാനമാണ് അമൂർത്ത എക്സ്പ്രഷനിസം . അന്താരാഷ്ട്ര സ്വാധീനം നേടുകയും ന്യൂയോർക്ക് നഗരത്തെ പാശ്ചാത്യ കലാ ലോകത്തിന്റെ കേന്ദ്രത്തിൽ ഉൾപ്പെടുത്തുകയും ചെയ്ത ആദ്യത്തെ അമേരിക്കൻ പ്രസ്ഥാനമാണിത്. മുമ്പ് പാരീസ് നിറച്ച ഈ പങ്ക്. "അമൂർത്ത എക്സ്പ്രഷനിസം" എന്ന പദം അമേരിക്കൻ കലയിൽ ആദ്യമായി കലാ നിരൂപകനായ റോബർട്ട് കോട്ട്സ് പ്രയോഗിച്ചെങ്കിലും, ജർമ്മൻ എക്സ്പ്രഷനിസത്തെക്കുറിച്ച് 1919 ൽ ജർമ്മനിയിൽ ആദ്യമായി ഡെർ സ്റ്റർം മാസികയിൽ ഇത് ഉപയോഗിച്ചു. അമേരിക്കൻ ഐക്യനാടുകളിൽ, വാസിലി കാൻഡിൻസ്കിയുടെ കൃതികളുമായി ബന്ധപ്പെട്ട് 1929 ൽ ആദ്യമായി ഈ പദം ഉപയോഗിച്ചതാണ് ആൽഫ്രഡ് ബാർ.
അമൂർത്ത പദപ്രയോഗം: 1940 കളിൽ ന്യൂയോർക്കിൽ വികസിപ്പിച്ച അമേരിക്കൻ പെയിന്റിംഗിലെ രണ്ടാം ലോക മഹായുദ്ധാനന്തര കലാ പ്രസ്ഥാനമാണ് അമൂർത്ത എക്സ്പ്രഷനിസം . അന്താരാഷ്ട്ര സ്വാധീനം നേടുകയും ന്യൂയോർക്ക് നഗരത്തെ പാശ്ചാത്യ കലാ ലോകത്തിന്റെ കേന്ദ്രത്തിൽ ഉൾപ്പെടുത്തുകയും ചെയ്ത ആദ്യത്തെ അമേരിക്കൻ പ്രസ്ഥാനമാണിത്. മുമ്പ് പാരീസ് നിറച്ച ഈ പങ്ക്. "അമൂർത്ത എക്സ്പ്രഷനിസം" എന്ന പദം അമേരിക്കൻ കലയിൽ ആദ്യമായി കലാ നിരൂപകനായ റോബർട്ട് കോട്ട്സ് പ്രയോഗിച്ചെങ്കിലും, ജർമ്മൻ എക്സ്പ്രഷനിസത്തെക്കുറിച്ച് 1919 ൽ ജർമ്മനിയിൽ ആദ്യമായി ഡെർ സ്റ്റർം മാസികയിൽ ഇത് ഉപയോഗിച്ചു. അമേരിക്കൻ ഐക്യനാടുകളിൽ, വാസിലി കാൻഡിൻസ്കിയുടെ കൃതികളുമായി ബന്ധപ്പെട്ട് 1929 ൽ ആദ്യമായി ഈ പദം ഉപയോഗിച്ചതാണ് ആൽഫ്രഡ് ബാർ.
അമൂർത്ത ഫാക്ടറി പാറ്റേൺ: അമൂർത്ത ഫാക്ടറി പാറ്റേൺ ഒരു കൂട്ടം വ്യക്തിഗത ഫാക്ടറികളുടെ കോൺക്രീറ്റ് ക്ലാസുകൾ വ്യക്തമാക്കാതെ ഒരു പൊതു തീം ഉൾക്കൊള്ളുന്ന ഒരു മാർഗ്ഗം ഉൾക്കൊള്ളുന്നു. സാധാരണ ഉപയോഗത്തിൽ, ക്ലയന്റ് സോഫ്റ്റ്വെയർ അമൂർത്ത ഫാക്ടറിയുടെ ഒരു ശക്തമായ നടപ്പാക്കൽ സൃഷ്ടിക്കുകയും തുടർന്ന് തീമിന്റെ ഭാഗമായ കോൺക്രീറ്റ് വസ്തുക്കൾ സൃഷ്ടിക്കുന്നതിന് ഫാക്ടറിയുടെ ജനറിക് ഇന്റർഫേസ് ഉപയോഗിക്കുകയും ചെയ്യുന്നു. ഈ ആന്തരിക ഫാക്ടറികളിൽ നിന്ന് ഏത് കോൺക്രീറ്റ് വസ്തുക്കൾ ലഭിക്കുന്നുവെന്ന് ക്ലയന്റിന് അറിയില്ല, കാരണം ഇത് അവരുടെ ഉൽപ്പന്നങ്ങളുടെ ജനറിക് ഇന്റർഫേസുകൾ മാത്രമേ ഉപയോഗിക്കുന്നുള്ളൂ. ഫാക്ടറി ഇന്റർഫേസിൽ തുറന്നുകാണിക്കുന്ന രീതികളിൽ ഒബ്ജക്റ്റ് സൃഷ്ടിക്കൽ നടപ്പിലാക്കുന്നതിനാൽ ഈ പാറ്റേൺ ഒരു കൂട്ടം ഒബ്ജക്റ്റുകൾ അവയുടെ പൊതുവായ ഉപയോഗത്തിൽ നിന്ന് വേർതിരിക്കുകയും ഒബ്ജക്റ്റ് കോമ്പോസിഷനെ ആശ്രയിക്കുകയും ചെയ്യുന്നു.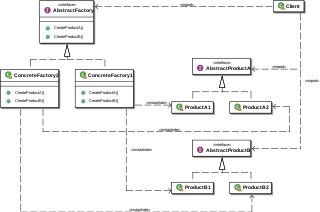
അമൂർത്ത ഫാക്ടറി പാറ്റേൺ: അമൂർത്ത ഫാക്ടറി പാറ്റേൺ ഒരു കൂട്ടം വ്യക്തിഗത ഫാക്ടറികളുടെ കോൺക്രീറ്റ് ക്ലാസുകൾ വ്യക്തമാക്കാതെ ഒരു പൊതു തീം ഉൾക്കൊള്ളുന്ന ഒരു മാർഗ്ഗം ഉൾക്കൊള്ളുന്നു. സാധാരണ ഉപയോഗത്തിൽ, ക്ലയന്റ് സോഫ്റ്റ്വെയർ അമൂർത്ത ഫാക്ടറിയുടെ ഒരു ശക്തമായ നടപ്പാക്കൽ സൃഷ്ടിക്കുകയും തുടർന്ന് തീമിന്റെ ഭാഗമായ കോൺക്രീറ്റ് വസ്തുക്കൾ സൃഷ്ടിക്കുന്നതിന് ഫാക്ടറിയുടെ ജനറിക് ഇന്റർഫേസ് ഉപയോഗിക്കുകയും ചെയ്യുന്നു. ഈ ആന്തരിക ഫാക്ടറികളിൽ നിന്ന് ഏത് കോൺക്രീറ്റ് വസ്തുക്കൾ ലഭിക്കുന്നുവെന്ന് ക്ലയന്റിന് അറിയില്ല, കാരണം ഇത് അവരുടെ ഉൽപ്പന്നങ്ങളുടെ ജനറിക് ഇന്റർഫേസുകൾ മാത്രമേ ഉപയോഗിക്കുന്നുള്ളൂ. ഫാക്ടറി ഇന്റർഫേസിൽ തുറന്നുകാണിക്കുന്ന രീതികളിൽ ഒബ്ജക്റ്റ് സൃഷ്ടിക്കൽ നടപ്പിലാക്കുന്നതിനാൽ ഈ പാറ്റേൺ ഒരു കൂട്ടം ഒബ്ജക്റ്റുകൾ അവയുടെ പൊതുവായ ഉപയോഗത്തിൽ നിന്ന് വേർതിരിക്കുകയും ഒബ്ജക്റ്റ് കോമ്പോസിഷനെ ആശ്രയിക്കുകയും ചെയ്യുന്നു.
അമൂർത്ത ഫാക്ടറി പാറ്റേൺ: അമൂർത്ത ഫാക്ടറി പാറ്റേൺ ഒരു കൂട്ടം വ്യക്തിഗത ഫാക്ടറികളുടെ കോൺക്രീറ്റ് ക്ലാസുകൾ വ്യക്തമാക്കാതെ ഒരു പൊതു തീം ഉൾക്കൊള്ളുന്ന ഒരു മാർഗ്ഗം ഉൾക്കൊള്ളുന്നു. സാധാരണ ഉപയോഗത്തിൽ, ക്ലയന്റ് സോഫ്റ്റ്വെയർ അമൂർത്ത ഫാക്ടറിയുടെ ഒരു ശക്തമായ നടപ്പാക്കൽ സൃഷ്ടിക്കുകയും തുടർന്ന് തീമിന്റെ ഭാഗമായ കോൺക്രീറ്റ് വസ്തുക്കൾ സൃഷ്ടിക്കുന്നതിന് ഫാക്ടറിയുടെ ജനറിക് ഇന്റർഫേസ് ഉപയോഗിക്കുകയും ചെയ്യുന്നു. ഈ ആന്തരിക ഫാക്ടറികളിൽ നിന്ന് ഏത് കോൺക്രീറ്റ് വസ്തുക്കൾ ലഭിക്കുന്നുവെന്ന് ക്ലയന്റിന് അറിയില്ല, കാരണം ഇത് അവരുടെ ഉൽപ്പന്നങ്ങളുടെ ജനറിക് ഇന്റർഫേസുകൾ മാത്രമേ ഉപയോഗിക്കുന്നുള്ളൂ. ഫാക്ടറി ഇന്റർഫേസിൽ തുറന്നുകാണിക്കുന്ന രീതികളിൽ ഒബ്ജക്റ്റ് സൃഷ്ടിക്കൽ നടപ്പിലാക്കുന്നതിനാൽ ഈ പാറ്റേൺ ഒരു കൂട്ടം ഒബ്ജക്റ്റുകൾ അവയുടെ പൊതുവായ ഉപയോഗത്തിൽ നിന്ന് വേർതിരിക്കുകയും ഒബ്ജക്റ്റ് കോമ്പോസിഷനെ ആശ്രയിക്കുകയും ചെയ്യുന്നു.
അമൂർത്ത ഫാക്ടറി പാറ്റേൺ: അമൂർത്ത ഫാക്ടറി പാറ്റേൺ ഒരു കൂട്ടം വ്യക്തിഗത ഫാക്ടറികളുടെ കോൺക്രീറ്റ് ക്ലാസുകൾ വ്യക്തമാക്കാതെ ഒരു പൊതു തീം ഉൾക്കൊള്ളുന്ന ഒരു മാർഗ്ഗം ഉൾക്കൊള്ളുന്നു. സാധാരണ ഉപയോഗത്തിൽ, ക്ലയന്റ് സോഫ്റ്റ്വെയർ അമൂർത്ത ഫാക്ടറിയുടെ ഒരു ശക്തമായ നടപ്പാക്കൽ സൃഷ്ടിക്കുകയും തുടർന്ന് തീമിന്റെ ഭാഗമായ കോൺക്രീറ്റ് വസ്തുക്കൾ സൃഷ്ടിക്കുന്നതിന് ഫാക്ടറിയുടെ ജനറിക് ഇന്റർഫേസ് ഉപയോഗിക്കുകയും ചെയ്യുന്നു. ഈ ആന്തരിക ഫാക്ടറികളിൽ നിന്ന് ഏത് കോൺക്രീറ്റ് വസ്തുക്കൾ ലഭിക്കുന്നുവെന്ന് ക്ലയന്റിന് അറിയില്ല, കാരണം ഇത് അവരുടെ ഉൽപ്പന്നങ്ങളുടെ ജനറിക് ഇന്റർഫേസുകൾ മാത്രമേ ഉപയോഗിക്കുന്നുള്ളൂ. ഫാക്ടറി ഇന്റർഫേസിൽ തുറന്നുകാണിക്കുന്ന രീതികളിൽ ഒബ്ജക്റ്റ് സൃഷ്ടിക്കൽ നടപ്പിലാക്കുന്നതിനാൽ ഈ പാറ്റേൺ ഒരു കൂട്ടം ഒബ്ജക്റ്റുകൾ അവയുടെ പൊതുവായ ഉപയോഗത്തിൽ നിന്ന് വേർതിരിക്കുകയും ഒബ്ജക്റ്റ് കോമ്പോസിഷനെ ആശ്രയിക്കുകയും ചെയ്യുന്നു.
അമൂർത്ത ഫാക്ടറി പാറ്റേൺ: അമൂർത്ത ഫാക്ടറി പാറ്റേൺ ഒരു കൂട്ടം വ്യക്തിഗത ഫാക്ടറികളുടെ കോൺക്രീറ്റ് ക്ലാസുകൾ വ്യക്തമാക്കാതെ ഒരു പൊതു തീം ഉൾക്കൊള്ളുന്ന ഒരു മാർഗ്ഗം ഉൾക്കൊള്ളുന്നു. സാധാരണ ഉപയോഗത്തിൽ, ക്ലയന്റ് സോഫ്റ്റ്വെയർ അമൂർത്ത ഫാക്ടറിയുടെ ഒരു ശക്തമായ നടപ്പാക്കൽ സൃഷ്ടിക്കുകയും തുടർന്ന് തീമിന്റെ ഭാഗമായ കോൺക്രീറ്റ് വസ്തുക്കൾ സൃഷ്ടിക്കുന്നതിന് ഫാക്ടറിയുടെ ജനറിക് ഇന്റർഫേസ് ഉപയോഗിക്കുകയും ചെയ്യുന്നു. ഈ ആന്തരിക ഫാക്ടറികളിൽ നിന്ന് ഏത് കോൺക്രീറ്റ് വസ്തുക്കൾ ലഭിക്കുന്നുവെന്ന് ക്ലയന്റിന് അറിയില്ല, കാരണം ഇത് അവരുടെ ഉൽപ്പന്നങ്ങളുടെ ജനറിക് ഇന്റർഫേസുകൾ മാത്രമേ ഉപയോഗിക്കുന്നുള്ളൂ. ഫാക്ടറി ഇന്റർഫേസിൽ തുറന്നുകാണിക്കുന്ന രീതികളിൽ ഒബ്ജക്റ്റ് സൃഷ്ടിക്കൽ നടപ്പിലാക്കുന്നതിനാൽ ഈ പാറ്റേൺ ഒരു കൂട്ടം ഒബ്ജക്റ്റുകൾ അവയുടെ പൊതുവായ ഉപയോഗത്തിൽ നിന്ന് വേർതിരിക്കുകയും ഒബ്ജക്റ്റ് കോമ്പോസിഷനെ ആശ്രയിക്കുകയും ചെയ്യുന്നു.
അമൂർത്ത ഫാക്ടറി പാറ്റേൺ: അമൂർത്ത ഫാക്ടറി പാറ്റേൺ ഒരു കൂട്ടം വ്യക്തിഗത ഫാക്ടറികളുടെ കോൺക്രീറ്റ് ക്ലാസുകൾ വ്യക്തമാക്കാതെ ഒരു പൊതു തീം ഉൾക്കൊള്ളുന്ന ഒരു മാർഗ്ഗം ഉൾക്കൊള്ളുന്നു. സാധാരണ ഉപയോഗത്തിൽ, ക്ലയന്റ് സോഫ്റ്റ്വെയർ അമൂർത്ത ഫാക്ടറിയുടെ ഒരു ശക്തമായ നടപ്പാക്കൽ സൃഷ്ടിക്കുകയും തുടർന്ന് തീമിന്റെ ഭാഗമായ കോൺക്രീറ്റ് വസ്തുക്കൾ സൃഷ്ടിക്കുന്നതിന് ഫാക്ടറിയുടെ ജനറിക് ഇന്റർഫേസ് ഉപയോഗിക്കുകയും ചെയ്യുന്നു. ഈ ആന്തരിക ഫാക്ടറികളിൽ നിന്ന് ഏത് കോൺക്രീറ്റ് വസ്തുക്കൾ ലഭിക്കുന്നുവെന്ന് ക്ലയന്റിന് അറിയില്ല, കാരണം ഇത് അവരുടെ ഉൽപ്പന്നങ്ങളുടെ ജനറിക് ഇന്റർഫേസുകൾ മാത്രമേ ഉപയോഗിക്കുന്നുള്ളൂ. ഫാക്ടറി ഇന്റർഫേസിൽ തുറന്നുകാണിക്കുന്ന രീതികളിൽ ഒബ്ജക്റ്റ് സൃഷ്ടിക്കൽ നടപ്പിലാക്കുന്നതിനാൽ ഈ പാറ്റേൺ ഒരു കൂട്ടം ഒബ്ജക്റ്റുകൾ അവയുടെ പൊതുവായ ഉപയോഗത്തിൽ നിന്ന് വേർതിരിക്കുകയും ഒബ്ജക്റ്റ് കോമ്പോസിഷനെ ആശ്രയിക്കുകയും ചെയ്യുന്നു.
അമൂർത്ത ഫാക്ടറി പാറ്റേൺ: അമൂർത്ത ഫാക്ടറി പാറ്റേൺ ഒരു കൂട്ടം വ്യക്തിഗത ഫാക്ടറികളുടെ കോൺക്രീറ്റ് ക്ലാസുകൾ വ്യക്തമാക്കാതെ ഒരു പൊതു തീം ഉൾക്കൊള്ളുന്ന ഒരു മാർഗ്ഗം ഉൾക്കൊള്ളുന്നു. സാധാരണ ഉപയോഗത്തിൽ, ക്ലയന്റ് സോഫ്റ്റ്വെയർ അമൂർത്ത ഫാക്ടറിയുടെ ഒരു ശക്തമായ നടപ്പാക്കൽ സൃഷ്ടിക്കുകയും തുടർന്ന് തീമിന്റെ ഭാഗമായ കോൺക്രീറ്റ് വസ്തുക്കൾ സൃഷ്ടിക്കുന്നതിന് ഫാക്ടറിയുടെ ജനറിക് ഇന്റർഫേസ് ഉപയോഗിക്കുകയും ചെയ്യുന്നു. ഈ ആന്തരിക ഫാക്ടറികളിൽ നിന്ന് ഏത് കോൺക്രീറ്റ് വസ്തുക്കൾ ലഭിക്കുന്നുവെന്ന് ക്ലയന്റിന് അറിയില്ല, കാരണം ഇത് അവരുടെ ഉൽപ്പന്നങ്ങളുടെ ജനറിക് ഇന്റർഫേസുകൾ മാത്രമേ ഉപയോഗിക്കുന്നുള്ളൂ. ഫാക്ടറി ഇന്റർഫേസിൽ തുറന്നുകാണിക്കുന്ന രീതികളിൽ ഒബ്ജക്റ്റ് സൃഷ്ടിക്കൽ നടപ്പിലാക്കുന്നതിനാൽ ഈ പാറ്റേൺ ഒരു കൂട്ടം ഒബ്ജക്റ്റുകൾ അവയുടെ പൊതുവായ ഉപയോഗത്തിൽ നിന്ന് വേർതിരിക്കുകയും ഒബ്ജക്റ്റ് കോമ്പോസിഷനെ ആശ്രയിക്കുകയും ചെയ്യുന്നു.
അമൂർത്ത ഫാക്ടറി പാറ്റേൺ: അമൂർത്ത ഫാക്ടറി പാറ്റേൺ ഒരു കൂട്ടം വ്യക്തിഗത ഫാക്ടറികളുടെ കോൺക്രീറ്റ് ക്ലാസുകൾ വ്യക്തമാക്കാതെ ഒരു പൊതു തീം ഉൾക്കൊള്ളുന്ന ഒരു മാർഗ്ഗം ഉൾക്കൊള്ളുന്നു. സാധാരണ ഉപയോഗത്തിൽ, ക്ലയന്റ് സോഫ്റ്റ്വെയർ അമൂർത്ത ഫാക്ടറിയുടെ ഒരു ശക്തമായ നടപ്പാക്കൽ സൃഷ്ടിക്കുകയും തുടർന്ന് തീമിന്റെ ഭാഗമായ കോൺക്രീറ്റ് വസ്തുക്കൾ സൃഷ്ടിക്കുന്നതിന് ഫാക്ടറിയുടെ ജനറിക് ഇന്റർഫേസ് ഉപയോഗിക്കുകയും ചെയ്യുന്നു. ഈ ആന്തരിക ഫാക്ടറികളിൽ നിന്ന് ഏത് കോൺക്രീറ്റ് വസ്തുക്കൾ ലഭിക്കുന്നുവെന്ന് ക്ലയന്റിന് അറിയില്ല, കാരണം ഇത് അവരുടെ ഉൽപ്പന്നങ്ങളുടെ ജനറിക് ഇന്റർഫേസുകൾ മാത്രമേ ഉപയോഗിക്കുന്നുള്ളൂ. ഫാക്ടറി ഇന്റർഫേസിൽ തുറന്നുകാണിക്കുന്ന രീതികളിൽ ഒബ്ജക്റ്റ് സൃഷ്ടിക്കൽ നടപ്പിലാക്കുന്നതിനാൽ ഈ പാറ്റേൺ ഒരു കൂട്ടം ഒബ്ജക്റ്റുകൾ അവയുടെ പൊതുവായ ഉപയോഗത്തിൽ നിന്ന് വേർതിരിക്കുകയും ഒബ്ജക്റ്റ് കോമ്പോസിഷനെ ആശ്രയിക്കുകയും ചെയ്യുന്നു.
ഭാഷകളുടെ അമൂർത്ത കുടുംബം: കമ്പ്യൂട്ടർ സയൻസിൽ, പ്രത്യേകിച്ചും formal പചാരിക ഭാഷാ സിദ്ധാന്തത്തിന്റെ മേഖലയിൽ, ഭാഷകളുടെ ഒരു അമൂർത്ത കുടുംബം എന്നത് സാധാരണ ഭാഷകൾക്കും സന്ദർഭ-രഹിത ഭാഷകൾക്കും ആവർത്തിച്ചുള്ള എണ്ണമറ്റ ഭാഷകൾക്കും പഠിച്ച formal പചാരിക ഭാഷകളുടെ മറ്റ് കുടുംബങ്ങൾക്കും പൊതുവായുള്ള സവിശേഷതകളെ സാമാന്യവൽക്കരിക്കുന്ന ഒരു അമൂർത്ത ഗണിതശാസ്ത്ര സങ്കൽപ്പമാണ്. ശാസ്ത്രസാഹിത്യത്തിൽ.
പ്രോപ്പർട്ടി സംഗ്രഹം: ഒരു പ്രത്യേക പാർസലുമായി ബന്ധപ്പെട്ട ഇടപാടുകൾ വിവരിക്കുന്ന നിയമപരമായ രേഖകളുടെ ഒരു ശേഖരമാണ് പ്രോപ്പർട്ടി അബ്‌സ്ട്രാക്റ്റ് . ഡീഡുകൾ, മോർട്ട്ഗേജുകൾ, വിൽപത്രം, പ്രോബേറ്റ് റെക്കോർഡുകൾ, കോടതി വ്യവഹാരങ്ങൾ, നികുതി വിൽപ്പന എന്നിവയെക്കുറിച്ചുള്ള പരാമർശങ്ങൾ സാധാരണയായി ഉൾപ്പെടുത്തിയിട്ടുണ്ട് - അടിസ്ഥാനപരമായി, സ്വത്തെ ബാധിക്കുന്ന ഏതെങ്കിലും നിയമ പ്രമാണം.
അമൂർത്ത ഗ്രാഫിക്കൽ ഡാറ്റ തരം: കമ്പ്യൂട്ടർ ഗ്രാഫിക്സിനായുള്ള ഒരു അമൂർത്ത ഡാറ്റാ തരത്തിന്റെ വിപുലീകരണമാണ് അമൂർത്ത ഗ്രാഫിക്കൽ ഡാറ്റ തരം ( എജിഡിടി ). എ.ജി.ഡി.ടികൾ എ.ഡി.ടികളുടെ ഗുണങ്ങൾ ഗ്രാഫിക്കൽ വസ്തുക്കൾ ഘടനാപരമായ രീതിയിൽ നിർമ്മിക്കാനുള്ള സൗകര്യങ്ങൾ നൽകുന്നു. G ദ്യോഗികമായി, ഒരു എജിഡിടിയെ "ഗ്രാഫിക്കൽ ഒബ്ജക്റ്റുകളുടെ ക്ലാസ്" എന്ന് നിർവചിക്കാം, അതിന്റെ ലോജിക്കൽ സ്വഭാവം ഒരു കൂട്ടം ഗ്രാഫിക്കൽ സ്വഭാവങ്ങളും ഒരു കൂട്ടം ഗ്രാഫിക്കൽ പ്രവർത്തനങ്ങളും നിർവചിക്കുന്നു.
ഗ്രൂപ്പ് സിദ്ധാന്തം: ഗണിതത്തിലും അമൂർത്ത ബീജഗണിതത്തിലും ഗ്രൂപ്പ് സിദ്ധാന്തം ഗ്രൂപ്പുകൾ എന്നറിയപ്പെടുന്ന ബീജഗണിത ഘടനകളെ പഠിക്കുന്നു. ഒരു ഗ്രൂപ്പിന്റെ ആശയം അമൂർത്ത ബീജഗണിതത്തിന്റെ കേന്ദ്രമാണ്: വളയങ്ങൾ, ഫീൽഡുകൾ, വെക്റ്റർ സ്പെയ്സുകൾ എന്നിവ പോലുള്ള മറ്റ് അറിയപ്പെടുന്ന ബീജഗണിത ഘടനകളെല്ലാം അധിക പ്രവർത്തനങ്ങളും പ്രപഞ്ചങ്ങളും ഉൾക്കൊള്ളുന്ന ഗ്രൂപ്പുകളായി കാണാൻ കഴിയും. ഗണിതത്തിലുടനീളം ഗ്രൂപ്പുകൾ ആവർത്തിക്കുന്നു, ഗ്രൂപ്പ് സിദ്ധാന്തത്തിന്റെ രീതികൾ ബീജഗണിതത്തിന്റെ പല ഭാഗങ്ങളെയും സ്വാധീനിച്ചിട്ടുണ്ട്. ലീനിയർ ബീജഗണിത ഗ്രൂപ്പുകളും ലീ ഗ്രൂപ്പുകളും ഗ്രൂപ്പ് സിദ്ധാന്തത്തിന്റെ രണ്ട് ശാഖകളാണ്, അവ മുന്നേറ്റങ്ങൾ അനുഭവിക്കുകയും അവരുടേതായ വിഷയ മേഖലകളായി മാറുകയും ചെയ്തു.
അമൂർത്ത തല: റഷ്യൻ എക്സ്പ്രഷനിസ്റ്റ് അലക്സെജ് വോൺ ജാവ്‌ലെൻസ്‌കിയുടെ ഓയിൽ പെയിന്റിംഗാണ് അബ്‌സ്ട്രാക്റ്റ് ഹെഡ് .
അമൂർത്ത മിഥ്യാധാരണ: 1967 ൽ കലാചരിത്രകാരിയും നിരൂപകനുമായ ബാർബറ റോസ് ആവിഷ്‌കരിച്ച അബ്‌സ്ട്രാക്റ്റ് മായവാദം. 1970 കളുടെ മധ്യത്തിൽ അമേരിക്കയിൽ പ്രചാരത്തിലുണ്ടായ ഒരു കലാപരമായ പ്രസ്ഥാനത്തെ നിർവചിക്കാൻ ലൂയിസ് കെ. മീസൽ സ്വതന്ത്രമായി ഈ പദം ഉപയോഗിച്ചു.
അമൂർത്ത ഇമാജിസ്റ്റുകൾ: 1961 ൽ ​​ന്യൂയോർക്കിലെ ഗുഗ്ഗൻഹൈം മ്യൂസിയത്തിൽ നടന്ന ഒരു എക്സിബിഷനിൽ നിന്ന് അമേരിക്കൻ അബ്‌സ്ട്രാക്റ്റ് എക്‌സ്‌പ്രഷനിസ്റ്റുകളും ഇമാജിസ്റ്റുകളും എന്ന പദത്തിൽ നിന്നാണ് ഉരുത്തിരിഞ്ഞത് . അമേരിക്കൻ, യൂറോപ്യൻ പെയിന്റിംഗ്, ശില്പം എന്നിവയിലെ പ്രവണതകളെക്കുറിച്ച് അന്വേഷിക്കുന്നതിനുള്ള പ്രോഗ്രാമുകളുടെ പരമ്പരയിലെ ആദ്യത്തേതാണ് ഈ എക്സിബിഷൻ.
അമൂർത്ത ഇമാജിസ്റ്റുകൾ: 1961 ൽ ​​ന്യൂയോർക്കിലെ ഗുഗ്ഗൻഹൈം മ്യൂസിയത്തിൽ നടന്ന ഒരു എക്സിബിഷനിൽ നിന്ന് അമേരിക്കൻ അബ്‌സ്ട്രാക്റ്റ് എക്‌സ്‌പ്രഷനിസ്റ്റുകളും ഇമാജിസ്റ്റുകളും എന്ന പദത്തിൽ നിന്നാണ് ഉരുത്തിരിഞ്ഞത് . അമേരിക്കൻ, യൂറോപ്യൻ പെയിന്റിംഗ്, ശില്പം എന്നിവയിലെ പ്രവണതകളെക്കുറിച്ച് അന്വേഷിക്കുന്നതിനുള്ള പ്രോഗ്രാമുകളുടെ പരമ്പരയിലെ ആദ്യത്തേതാണ് ഈ എക്സിബിഷൻ.
അമൂർത്ത ഇംപ്രഷനിസം: 1940 കളിൽ ന്യൂയോർക്ക് സിറ്റിയിൽ ആരംഭിച്ച ഒരു കലാ പ്രസ്ഥാനമാണ് അമൂർത്ത ഇംപ്രഷനിസം . ഇംപ്രഷനിസ്റ്റ് ശൈലിയിൽ യഥാർത്ഥ ജീവിത രംഗങ്ങൾ, വസ്തുക്കൾ അല്ലെങ്കിൽ ആളുകൾ (ഛായാചിത്രങ്ങൾ) പോലുള്ള ഒരു വിഷയത്തിന്റെ പെയിന്റിംഗ് ഇതിൽ ഉൾപ്പെടുന്നു, എന്നാൽ വ്യത്യസ്ത അമൂർത്ത നടപടികൾക്ക് emphas ന്നൽ നൽകുന്നു. പെയിന്റിംഗുകൾ പലപ്പോഴും പെയിന്റ് ചെയ്യുന്നത് എൻ പ്ലെയിൻ എയർ ആണ്, ആർട്ടിസ്റ്റിന് മുന്നിൽ ലാൻഡ്സ്കേപ്പിനൊപ്പം നേരിട്ട് പെയിന്റിംഗ് ഉൾപ്പെടുന്ന ഒരു കലാപരമായ ശൈലി. ശുദ്ധമായ അമൂർത്തതയുടെ വരകൾക്കും പെയിന്റിംഗിലെ യാഥാർത്ഥ്യത്തിന്റെ ഒരു അലവൻസ് അലവൻസുകൾക്കുമിടയിൽ ഈ ചലനം അതിമനോഹരമായി പ്രവർത്തിക്കുന്നു.
അമൂർത്ത ഇംപ്രഷനിസം: 1940 കളിൽ ന്യൂയോർക്ക് സിറ്റിയിൽ ആരംഭിച്ച ഒരു കലാ പ്രസ്ഥാനമാണ് അമൂർത്ത ഇംപ്രഷനിസം . ഇംപ്രഷനിസ്റ്റ് ശൈലിയിൽ യഥാർത്ഥ ജീവിത രംഗങ്ങൾ, വസ്തുക്കൾ അല്ലെങ്കിൽ ആളുകൾ (ഛായാചിത്രങ്ങൾ) പോലുള്ള ഒരു വിഷയത്തിന്റെ പെയിന്റിംഗ് ഇതിൽ ഉൾപ്പെടുന്നു, എന്നാൽ വ്യത്യസ്ത അമൂർത്ത നടപടികൾക്ക് emphas ന്നൽ നൽകുന്നു. പെയിന്റിംഗുകൾ പലപ്പോഴും പെയിന്റ് ചെയ്യുന്നത് എൻ പ്ലെയിൻ എയർ ആണ്, ആർട്ടിസ്റ്റിന് മുന്നിൽ ലാൻഡ്സ്കേപ്പിനൊപ്പം നേരിട്ട് പെയിന്റിംഗ് ഉൾപ്പെടുന്ന ഒരു കലാപരമായ ശൈലി. ശുദ്ധമായ അമൂർത്തതയുടെ വരകൾക്കും പെയിന്റിംഗിലെ യാഥാർത്ഥ്യത്തിന്റെ ഒരു അലവൻസ് അലവൻസുകൾക്കുമിടയിൽ ഈ ചലനം അതിമനോഹരമായി പ്രവർത്തിക്കുന്നു.
യൂണികോർ: സൂപ്പർ കമ്പ്യൂട്ടറുകൾ അല്ലെങ്കിൽ ക്ലസ്റ്റർ സിസ്റ്റങ്ങൾ, ഡാറ്റാബേസുകളിൽ സംഭരിച്ചിരിക്കുന്ന വിവരങ്ങൾ എന്നിവ പോലുള്ള വിഭവങ്ങൾക്കായുള്ള ഒരു ഗ്രിഡ് കമ്പ്യൂട്ടിംഗ് സാങ്കേതികവിദ്യയാണ് യൂണികോർ . ജർമ്മൻ വിദ്യാഭ്യാസ മന്ത്രാലയത്തിന്റെ (ബിഎംബിഎഫ്) ധനസഹായത്തോടെ രണ്ട് പദ്ധതികളിലാണ് യൂണികോർ വികസിപ്പിച്ചത്. യൂറോപ്യൻ ധനസഹായമുള്ള പ്രോജക്റ്റുകളിൽ നിരവധി സൂപ്പർ കമ്പ്യൂട്ടർ കേന്ദ്രങ്ങളിൽ ഉപയോഗിക്കുന്ന ഒരു മിഡിൽവെയർ സിസ്റ്റമായി യൂണികോർ പരിണമിച്ചു. മറ്റ് ഗവേഷണ പ്രോജക്ടുകളിൽ യുണിക്കോർ ഒരു അടിസ്ഥാനമായി പ്രവർത്തിച്ചു. ബി‌എസ്‌ഡി ലൈസൻസിന് കീഴിലുള്ള ഓപ്പൺ സോഴ്‌സാണ് യൂണികോർ സാങ്കേതികവിദ്യ, അത് സോഴ്‌സ്ഫോർജിൽ ലഭ്യമാണ്.
അമൂർത്ത എൽ-സ്പേസ്: ഗണിതശാസ്ത്രത്തിൽ, പ്രത്യേകിച്ചും ഓർഡർ തിയറിയിലും ഫംഗ്ഷണൽ വിശകലനത്തിലും, ഒരു അമൂർത്ത എൽ- സ്പേസ് , ഒരു എഎൽ-സ്പേസ് അല്ലെങ്കിൽ ഒരു അമൂർത്ത ലെബസ്ഗു സ്പേസ് ഒരു ബനാച്ച് ലാറ്റിസ് ആണ് X ന്റെ പോസിറ്റീവ് കോണിൽ ആഡിറ്റീവാണ് ആരുടെ മാനദണ്ഡം.
അമൂർത്ത ലോജിക് (ആൽബം): ബാസിസ്റ്റ് ജോനാസ് ഹെൽ‌ബോർഗും ഗിറ്റാറിസ്റ്റ് ഷാൻ ലെയ്‌നും ചേർന്നുള്ള ആദ്യത്തെ സഹകരണ ലൈവ് ആൽബമാണ് അമൂർത്ത ലോജിക് , 1995 ൽ ഡേ എട്ട് മ്യൂസിക് വഴി പുറത്തിറങ്ങി; പുതുക്കിയ ട്രാക്ക് ലിസ്റ്റിംഗും രണ്ട് അധിക ട്രാക്കുകളും അടങ്ങിയ പുനർ‌നിർമ്മിച്ചതും പുനർ‌നിർമ്മിച്ചതുമായ ഒരു പതിപ്പ് 2004 ൽ ബാർ‌ഡോ റെക്കോർ‌ഡ്സ് വഴി വീണ്ടും വിതരണം ചെയ്തു. ഈ ലൈനപ്പിനായി, ഡ്രമ്മർ കോഫി ബേക്കറും അവരോടൊപ്പം ചേരുന്നു.
അമൂർത്ത ലോജിക് (ആൽബം): ബാസിസ്റ്റ് ജോനാസ് ഹെൽ‌ബോർഗും ഗിറ്റാറിസ്റ്റ് ഷാൻ ലെയ്‌നും ചേർന്നുള്ള ആദ്യത്തെ സഹകരണ ലൈവ് ആൽബമാണ് അമൂർത്ത ലോജിക് , 1995 ൽ ഡേ എട്ട് മ്യൂസിക് വഴി പുറത്തിറങ്ങി; പുതുക്കിയ ട്രാക്ക് ലിസ്റ്റിംഗും രണ്ട് അധിക ട്രാക്കുകളും അടങ്ങിയ പുനർ‌നിർമ്മിച്ചതും പുനർ‌നിർമ്മിച്ചതുമായ ഒരു പതിപ്പ് 2004 ൽ ബാർ‌ഡോ റെക്കോർ‌ഡ്സ് വഴി വീണ്ടും വിതരണം ചെയ്തു. ഈ ലൈനപ്പിനായി, ഡ്രമ്മർ കോഫി ബേക്കറും അവരോടൊപ്പം ചേരുന്നു.
അമൂർത്ത ലോജിക്സ്: ജാസ് ഫ്യൂഷൻ, ലോകം, ജാം ബാൻഡ് സംഗീതം എന്നിവയിൽ പ്രത്യേകതയുള്ള നോർത്ത് കരോലിന ആസ്ഥാനമായുള്ള റെക്കോർഡ് ലേബലാണ് അമൂർത്ത ലോജിക്സ് . 2018 വരെ, ലോകമെമ്പാടുമുള്ള സംഗീതജ്ഞരിൽ നിന്ന് അമ്പതിലധികം ശീർഷകങ്ങൾ അബ്‌സ്ട്രാക്റ്റ് ലോജിക്സ് പുറത്തിറക്കിയിരുന്നു. 2019 ൽ ജാസ് ടൈംസ് മാഗസിൻ റീഡേഴ്സ് പോളിൽ "മികച്ച റെക്കോർഡ് ലേബൽ" ആയി തിരഞ്ഞെടുക്കപ്പെട്ടു.
അമൂർത്ത യന്ത്രം: ഒരു അമൂർത്ത കമ്പ്യൂട്ടർ എന്നും വിളിക്കപ്പെടുന്ന ഒരു അമൂർത്ത യന്ത്രം ഒരു കമ്പ്യൂട്ടർ മാതൃക നിർവചിക്കാൻ ഉപയോഗിക്കുന്ന ഒരു സൈദ്ധാന്തിക കമ്പ്യൂട്ടറാണ്. കമ്പ്യൂട്ടർ സയൻസ്, കമ്പ്യൂട്ടർ എഞ്ചിനീയറിംഗ് വിഭാഗങ്ങളിൽ കമ്പ്യൂട്ടിംഗ് പ്രക്രിയകളുടെ സംഗ്രഹം ഉപയോഗിക്കുന്നു, മാത്രമല്ല ഇത് ഒരു പ്രത്യേക സമയ മാതൃകയെ കണക്കാക്കുന്നു.
മാനിഫോൾഡ്: ഗണിതശാസ്ത്രത്തിൽ, ഓരോ പോയിന്റിനും സമീപമുള്ള യൂക്ലിഡിയൻ സ്ഥലവുമായി പ്രാദേശികമായി സാമ്യമുള്ള ഒരു ടോപ്പോളജിക്കൽ സ്പേസ് ആണ് മാനിഫോൾഡ് . കൂടുതൽ കൃത്യമായി, ഒരു n -ദിമെംസിഒനല് പലമടങ്ങ്, അല്ലെങ്കിൽ n ചുരുക്കത്തിൽ -മനിഫൊല്ദ്, ഓരോ പോയിന്റ് അളവിനും എന്ന യൂക്ലിഡിയൻ വരെ ഹൊമെഒമൊര്ഫിച് n ലേക്കുള്ള സമീപസ്ഥലങ്ങൾ ഉണ്ടെന്ന് പ്രോപ്പർട്ടി ഗുണനവും സ്ഥലം.
ശുദ്ധമായ ഗണിതശാസ്ത്രം: ഗണിതശാസ്ത്രത്തിന് പുറത്തുള്ള ഏതൊരു ആപ്ലിക്കേഷനിൽ നിന്നും സ്വതന്ത്രമായി ഗണിതശാസ്ത്ര ആശയങ്ങളെക്കുറിച്ചുള്ള പഠനമാണ് ശുദ്ധമായ ഗണിതശാസ്ത്രം. ഈ ആശയങ്ങൾ യഥാർത്ഥ ലോകത്തിലെ ആശങ്കകളിൽ നിന്ന് ഉത്ഭവിച്ചേക്കാം, ലഭിച്ച ഫലങ്ങൾ പിന്നീട് പ്രായോഗിക പ്രയോഗങ്ങൾക്ക് ഉപയോഗപ്രദമാകും, പക്ഷേ ശുദ്ധമായ ഗണിതശാസ്ത്രജ്ഞർ പ്രാഥമികമായി അത്തരം ആപ്ലിക്കേഷനുകളാൽ പ്രചോദിതരല്ല. പകരം, അടിസ്ഥാന തത്വങ്ങളുടെ യുക്തിസഹമായ പ്രത്യാഘാതങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള ബൗദ്ധിക വെല്ലുവിളിയും സൗന്ദര്യാത്മക സൗന്ദര്യവുമാണ് അപ്പീലിന് കാരണം.
അമൂർത്ത അർത്ഥ പ്രാതിനിധ്യം: ഒരു സെമാന്റിക് പ്രാതിനിധ്യ ഭാഷയാണ് അമൂർത്ത അർത്ഥ പ്രതിനിധാനം ( AMR ). എ‌എം‌ആർ‌ ഗ്രാഫുകൾ‌ റൂട്ട്, ലേബൽ‌, ഡയറക്‍ട്, അസൈക്ലിക് ഗ്രാഫുകൾ‌ (ഡി‌എ‌ജി), മുഴുവൻ വാക്യങ്ങളും ഉൾക്കൊള്ളുന്നു. വാക്യഘടന പ്രാതിനിധ്യങ്ങളിൽ നിന്ന് വിട്ടുനിൽക്കാനാണ് അവ ഉദ്ദേശിക്കുന്നത്, അർത്ഥത്തിൽ സമാനമായ വാക്യങ്ങൾ ഒരേ വാക്കിൽ ഇല്ലെങ്കിലും, ഒരേ എ‌എം‌ആർ നൽകണം. സ്വഭാവമനുസരിച്ച്, എ‌എം‌ആർ ഭാഷ ഇംഗ്ലീഷിനോട് പക്ഷപാതപരമാണ് - ഇത് ഒരു അന്താരാഷ്ട്ര സഹായ ഭാഷയായി പ്രവർത്തിക്കാൻ ഉദ്ദേശിച്ചുള്ളതല്ല.
സമ്പൂർണ്ണ സംഗീതം: ഒന്നിനെക്കുറിച്ചും വ്യക്തമായി "പറയാത്ത" സംഗീതമാണ് സമ്പൂർണ്ണ സംഗീതം ; പ്രോഗ്രാം സംഗീതത്തിന് വിപരീതമായി, അത് പ്രാതിനിധ്യമില്ലാത്തതാണ്. 18-ആം നൂറ്റാണ്ടിന്റെ അവസാനത്തിൽ ജർമ്മൻ റൊമാന്റിസിസത്തിന്റെ രചയിതാക്കളായ വിൽഹെം ഹെൻ‌റിക് വാക്കൻ‌റോഡർ, ലുഡ്‌വിഗ് ടിക്, ഇടി‌എ ഹോഫ്മാൻ എന്നിവരുടെ രചനകളിൽ കേവല സംഗീതത്തെക്കുറിച്ചുള്ള ആശയം വികസിപ്പിച്ചെങ്കിലും 1846 വരെ ഈ പദം ഉപയോഗിച്ചിരുന്നില്ല, അവിടെ ആദ്യമായി റിച്ചാർഡ് വാഗ്നർ ഉപയോഗിച്ചു ബീറ്റോവന്റെ ഒമ്പതാമത്തെ സിംഫണിയിലേക്കുള്ള ഒരു പ്രോഗ്രാമിൽ.
വെബ് ഓന്റോളജി ഭാഷ: ഒന്റോളജികൾ രചിക്കുന്നതിനുള്ള വിജ്ഞാന പ്രാതിനിധ്യ ഭാഷകളുടെ ഒരു കുടുംബമാണ് വെബ് ഒന്റോളജി ലാംഗ്വേജ് ( OWL ). വിവിധ ഡൊമെയ്‌നുകളുടെ അറിവിന്റെ ഘടനയെ നിർവചിക്കുന്ന ടാക്‌സോണമി, വർഗ്ഗീകരണ നെറ്റ്‌വർക്കുകൾ എന്നിവ വിവരിക്കുന്നതിനുള്ള ഒരു way പചാരിക മാർഗമാണ് ഒന്റോളജികൾ: ഒബ്ജക്റ്റുകളുടെ ക്ലാസുകളെ പ്രതിനിധീകരിക്കുന്ന നാമങ്ങൾ, വസ്തുക്കൾ തമ്മിലുള്ള ബന്ധത്തെ പ്രതിനിധീകരിക്കുന്ന ക്രിയകൾ.
അമൂർത്തമായ ഒബ്ജക്റ്റ് സിദ്ധാന്തം: അമൂർത്ത വസ്തുക്കളെ സംബന്ധിച്ച മെറ്റാഫിസിക്‌സിന്റെ ഒരു ശാഖയാണ് അബ്‌സ്ട്രാക്റ്റ് ഒബ്ജക്റ്റ് തിയറി ( AOT ). 1981 ൽ മെറ്റാഫിഷ്യൻ എഡ്വേർഡ് സാൽറ്റ ആവിഷ്കരിച്ച ഈ സിദ്ധാന്തം ഗണിതശാസ്ത്ര പ്ലാറ്റോണിസത്തിന്റെ വികാസമായിരുന്നു.
അമൂർത്ത ഓർക്കസ്ട്ര: റോബ് മിച്ചൽ 2011 ൽ സൃഷ്ടിച്ച ബ്രിട്ടീഷ് ഹിപ്-ഹോപ്പ് സംഗീത ഗ്രൂപ്പാണ് അബ്‌സ്ട്രാക്റ്റ് ഓർക്കസ്ട്ര . സ്വതന്ത്ര റെക്കോർഡ് ലേബലായ എടി‌എ റെക്കോർഡിലേക്ക് ഗ്രൂപ്പ് ഒപ്പിട്ടു. അബ്‌സ്ട്രാക്റ്റ് ഓർക്കസ്ട്ര അഞ്ച് സ്റ്റുഡിയോ ആൽബങ്ങൾ പുറത്തിറക്കി, ദില്ല (2017), മാഡ്‌വില്ലിൻ വോളിയം. 1 (2018), മാഡ്‌വില്ലിൻ വോളിയം. 2 (2019), ഫന്റാസ്റ്റിക് 2020 വാല്യം. 1 (2019), ഫന്റാസ്റ്റിക് 2020 വോളിയം. 2 (2019), അഞ്ച് സിംഗിൾസ്, ന്യൂ ഡേ (2017), ഫാൻസി ക്ല own ൺ (2018), എയർ അടി എംഎഫ് ഡൂം (2019), പ്രാർത്ഥിക്കുക (2020), അസൂയ (2020). "സമന്വയം അവരുടെ വ്യതിരിക്തമായ ശബ്ദത്തിന് പേരുകേട്ടതാണ്, ഇത് എക്കാലത്തെയും പ്രശസ്തമായ ചില ഹിപ്-ഹോപ്പ് നിർമ്മാണങ്ങളെ ബിഗ് ബാൻഡ് ജാസ്, ലൈവ് ഹിപ്-ഹോപ്പ് എന്നിവയുടെ അദ്വിതീയ മിശ്രിതമാക്കി പുനർവ്യാഖ്യാനം ചെയ്യുന്നു".
ശബ്ദ കവിത: സാഹിത്യ-സംഗീത രചനയെ ബന്ധിപ്പിക്കുന്ന ഒരു കലാരൂപമാണ് ശബ്ദ കവിത , അതിൽ കൂടുതൽ പരമ്പരാഗത സെമാന്റിക്, വാക്യഘടന മൂല്യങ്ങൾക്ക് പകരം മനുഷ്യന്റെ സംഭാഷണത്തിന്റെ സ്വരസൂചക വശങ്ങൾ മുൻ‌കൂട്ടി നിശ്ചയിച്ചിട്ടുണ്ട്; "വാക്കുകളില്ലാത്ത വാക്യം". നിർവചനം അനുസരിച്ച്, ശബ്ദ കവിത പ്രധാനമായും പ്രകടനത്തെ ഉദ്ദേശിച്ചുള്ളതാണ്.
ഫറാസ് അൻവർ: പാകിസ്താൻ സംഗീതജ്ഞൻ, സംഗീതസംവിധായകൻ, ഗായകൻ-ഗാനരചയിതാവ്, ബാൻഡ്‌ലീഡർ, മിസ്രാബ് സ്ഥാപിച്ച ഗിറ്റാറിസ്റ്റ് എന്നിവരാണ് ഫറാസ് അൻവർ - പാക്കിസ്ഥാൻ ആസ്ഥാനമായി പ്രവർത്തിക്കുന്ന ഹെവി മെറ്റൽ സംഗീതവും ഹാർഡ് റോക്ക് വിഭാഗവും. ഇലക്ട്രിക് ഗിറ്റാറിലെ അദ്ദേഹത്തിന്റെ സംഗീത പ്രവർത്തനം രാജ്യത്തെ സംഗീത വിമർശകർ "പാകിസ്ഥാന്റെ പുരോഗമന പാറയുടെ മാസ്റ്റർ" എന്ന് വിശേഷിപ്പിച്ചിരിക്കുന്നു. അൻവർ നിലവിൽ ലയൺ മ്യൂസിക്ക് - ഫിന്നിഷ് നിർമ്മാണ, റെക്കോർഡ് ലേബൽ കമ്പനിയാണ്.
അമൂർത്ത കാഴ്ചപ്പാട്: ഗിറ്റാറിസ്റ്റ് ഫറാസ് അൻവറിന്റെ സ്റ്റുഡിയോ ആൽബമാണ് അബ്‌സ്ട്രാക്റ്റ് പോയിന്റ് ഓഫ് വ്യൂ , 2001 ഡിസംബറിൽ ഗ്നാർലി ഗീസർ റെക്കോർഡ്സ് വഴി പുറത്തിറക്കി 2004 സെപ്റ്റംബർ 21 ന് ലയൺ മ്യൂസിക് വഴി വീണ്ടും പുറത്തിറക്കി.
അവരുടെ യുക്തിപരമായ തീവ്രതകളിലേക്ക് എടുത്ത അമൂർത്ത തത്വങ്ങൾ: ഇംഗ്ലണ്ടിലെ ലണ്ടനിൽ നിന്നുള്ള ഡെത്ത് മെറ്റൽ ബാൻഡായ ഡാർക്ക് ഹെറസിയുടെ ഏക ആൽബമാണ് അമൂർത്ത തത്ത്വങ്ങൾ അവരുടെ യുക്തിസഹമായ തീവ്രത 1995 ൽ പുറത്തിറങ്ങിയത്.
അമൂർത്ത മാറ്റിയെഴുത്ത് യന്ത്രം: ചുരുങ്ങിയ ടേം റീറൈറ്റിംഗ് സിസ്റ്റങ്ങൾക്കായി ടേം റീറൈറ്റിംഗ് നടപ്പിലാക്കുന്ന ഒരു വെർച്വൽ മെഷീനാണ് അബ്‌സ്ട്രാക്റ്റ് റീറൈറ്റിംഗ് മെഷീൻ (ARM).
അമൂർത്തമായ പരുക്കൻ: കാലിഫോർണിയയിലെ ലോസ് ഏഞ്ചൽസിൽ നിന്നുള്ള റാപ്പറാണ് ആരോൺ പോയിന്റർ .
സെൻസ് ഡാറ്റ: ഇരുപതാം നൂറ്റാണ്ടിന്റെ തുടക്കത്തിൽ ബെർട്രാൻഡ് റസ്സൽ, സിഡി ബ്രോഡ്, എച്ച് എച്ച് പ്രൈസ്, എ ജെ അയർ, ജി ഇ മൂർ തുടങ്ങിയ തത്ത്വചിന്തകർ പ്രചാരത്തിലുണ്ടായിരുന്ന ഗർഭധാരണ തത്ത്വചിന്തയിലെ ഒരു കാഴ്ചയാണ് സെൻസ് ഡാറ്റയുടെ സിദ്ധാന്തം. ഇന്ദ്രിയ ഡാറ്റയെ മനസ്സിനെ ആശ്രയിച്ചുള്ള വസ്‌തുക്കളായി കണക്കാക്കുന്നു, അവയുടെ നിലനിൽപ്പും ഗുണങ്ങളും ഗർഭധാരണത്തിൽ നമുക്ക് നേരിട്ട് അറിയാം. ഈ വസ്‌തുക്കൾ മനസിനുള്ളിലെ വിശകലനം ചെയ്യാത്ത അനുഭവങ്ങളാണ്, അവ തുടർന്നുള്ള കൂടുതൽ വിപുലമായ മാനസിക പ്രവർത്തനങ്ങൾക്ക് ദൃശ്യമാകുന്നു.
അമൂർത്ത ലളിതമായ സങ്കീർണ്ണത: കോമ്പിനേറ്ററിക്സിൽ, ഒരു അമൂർത്ത സിംപ്ലിസിയൽ കോംപ്ലക്സ് (എ‌എസ്‌സി) എന്നത് ഒരു കൂട്ടം സെറ്റുകളാണ്, അത് ഉപസെറ്റുകൾ എടുക്കുന്നതിനനുസരിച്ച് അടച്ചിരിക്കുന്നു, അതായത്, കുടുംബത്തിലെ ഒരു സെറ്റിന്റെ എല്ലാ ഉപസെറ്റുകളും കുടുംബത്തിലുണ്ട്. ലളിതമായ ഒരു സമുച്ചയത്തിന്റെ ജ്യാമിതീയ സങ്കൽപ്പത്തിന്റെ പൂർണ്ണമായും സംയോജിത വിവരണമാണിത്. ഉദാഹരണത്തിന്, ഒരു ദ്വിമാന ലളിതമായ സമുച്ചയത്തിൽ, കുടുംബത്തിലെ സെറ്റുകൾ ത്രികോണങ്ങൾ, അവയുടെ അരികുകൾ, അവയുടെ ലംബങ്ങൾ എന്നിവയാണ്.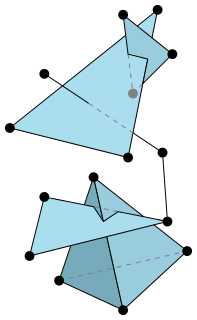
അമൂർത്ത വേഗത + ശബ്‌ദം: ഇറ്റാലിയൻ ഫ്യൂച്ചറിസ്റ്റ് ചിത്രകാരനായ ജിയാക്കോമോ ബല്ലയുടെ ചിത്രമാണ് അബ്‌സ്ട്രാക്റ്റ് സ്പീഡ് + സൗണ്ട് , 1913–14 ൽ ആർട്ടിസ്റ്റ് സൃഷ്ടിച്ച ചലനത്തെക്കുറിച്ചുള്ള നിരവധി പഠനങ്ങളിൽ ഒന്ന്. അബ്സ്ട്രാക്റ്റ് സ്പീഡ് (1913) മുതൽ അബ്‌സ്ട്രാക്റ്റ് സ്പീഡ് - ദി കാർ ഹാസ് പാസ് (1913) എന്ന് അവസാനിക്കുന്ന ഒരു ലാൻഡ്‌സ്‌കേപ്പിലൂടെ ഒരു റേസിംഗ് കാർ കടന്നുപോകുന്നത് വിവരിക്കുന്ന ഒരു ട്രിപ്റ്റിച്ചിലെ രണ്ടാമത്തെ ചിത്രമാണിത്. മൂന്ന് പെയിന്റിംഗുകൾ ഒരൊറ്റ ലാൻഡ്‌സ്‌കേപ്പിന്റെ സൂചനകൾ പങ്കിടുന്നു, ഓരോ പെയിന്റിംഗും അതിന്റെ ഫ്രെയിമിൽ തുടരുന്നു.
അമൂർത്ത സ്റ്റേറ്റ് മെഷീൻ: കമ്പ്യൂട്ടർ സയൻസിൽ, അനിയന്ത്രിതമായ ഡാറ്റാ ഘടനകളുള്ള സംസ്ഥാനങ്ങളിൽ പ്രവർത്തിക്കുന്ന ഒരു സ്റ്റേറ്റ് മെഷീനാണ് അമൂർത്ത സ്റ്റേറ്റ് മെഷീൻ ( ASM ).
അമൂർത്ത സംസ്ഥാന യന്ത്ര ഭാഷ: മൈക്രോസോഫ്റ്റ് വികസിപ്പിച്ചെടുത്ത അമൂർത്ത സ്റ്റേറ്റ് മെഷീനുകളുടെ formal പചാരിക രീതിയെ അടിസ്ഥാനമാക്കിയുള്ള ഒരു പ്രോഗ്രാമിംഗ് ഭാഷയാണ് അബ്‌സ്ട്രാക്റ്റ് സ്റ്റേറ്റ് മെഷീൻ ലാംഗ്വേജ് ( AsmL ). AsmL ഒരു പ്രവർത്തന ഭാഷയാണ്.
അമൂർത്ത സ്റ്റേറ്റ് മെഷീൻ: കമ്പ്യൂട്ടർ സയൻസിൽ, അനിയന്ത്രിതമായ ഡാറ്റാ ഘടനകളുള്ള സംസ്ഥാനങ്ങളിൽ പ്രവർത്തിക്കുന്ന ഒരു സ്റ്റേറ്റ് മെഷീനാണ് അമൂർത്ത സ്റ്റേറ്റ് മെഷീൻ ( ASM ).
ടെറി മൂർ (കാർട്ടൂണിസ്റ്റ്): അമേരിക്കൻ കാർട്ടൂണിസ്റ്റാണ് ടെറി മൂർ , അപരിചിതർ ഇൻ പാരഡൈസ് , റേച്ചൽ റൈസിംഗ് , ഹോമേജ് കോമിക്സിന്റെ സ്ഥാപനം എന്നിവയ്ക്ക് പേരുകേട്ടതാണ്.
ക്രിസ്റ്റോഫ് നെയ്മാൻ: ക്രിസ്റ്റോഫ് നെയ്മാൻ ഒരു ചിത്രകാരൻ, ഗ്രാഫിക് ഡിസൈനർ, കുട്ടികളുടെ പുസ്തക രചയിതാവ്.
അമൂർത്ത വാക്യഘടന: കമ്പ്യൂട്ടർ സയൻസിൽ, ഏതെങ്കിലും പ്രത്യേക പ്രാതിനിധ്യത്തിൽ നിന്നോ എൻകോഡിംഗിൽ നിന്നോ വിഭിന്നമായി ഡാറ്റാ തരമായി വിവരിച്ചിരിക്കുന്ന അതിന്റെ ഘടനയാണ് ഡാറ്റയുടെ അമൂർത്ത വാക്യഘടന . കമ്പ്യൂട്ടർ ഭാഷകളിലെ വാചകത്തിന്റെ പ്രാതിനിധ്യത്തിൽ ഇത് പ്രത്യേകിച്ചും ഉപയോഗിക്കുന്നു, അവ സാധാരണയായി ഒരു ട്രീ ഘടനയിൽ ഒരു അമൂർത്ത വാക്യഘടന ട്രീ ആയി സൂക്ഷിക്കുന്നു. ഡാറ്റയുടെ ഘടന മാത്രം ഉൾക്കൊള്ളുന്ന അമൂർത്ത വാക്യഘടന കോൺക്രീറ്റ് വാക്യഘടനയുമായി വിഭിന്നമാണ്, അതിൽ പ്രാതിനിധ്യത്തെക്കുറിച്ചുള്ള വിവരങ്ങളും ഉൾപ്പെടുന്നു. ഉദാഹരണത്തിന്, കോൺക്രീറ്റ് വാക്യഘടനയിൽ പരാൻതീസിസ് അല്ലെങ്കിൽ കോമ പോലുള്ള സവിശേഷതകൾ ഉൾപ്പെടുന്നു, അവ അമൂർത്ത വാക്യഘടനയിൽ ഉൾപ്പെടുത്തിയിട്ടില്ല, കാരണം അവ ഘടനയിൽ ഉൾക്കൊള്ളുന്നു.
ASN.1: ക്രോസ്-പ്ലാറ്റ്ഫോം രീതിയിൽ സീരിയലൈസ് ചെയ്യാനും ഡിസീരിയലൈസ് ചെയ്യാനും കഴിയുന്ന ഡാറ്റാ ഘടനകളെ നിർവചിക്കുന്നതിനുള്ള ഒരു സ്റ്റാൻഡേർഡ് ഇന്റർഫേസ് വിവരണ ഭാഷയാണ് അമൂർത്ത സിന്റാക്സ് നൊട്ടേഷൻ വൺ ( ASN.1 ). ടെലികമ്മ്യൂണിക്കേഷൻ, കമ്പ്യൂട്ടർ നെറ്റ്‌വർക്കിംഗ്, പ്രത്യേകിച്ച് ക്രിപ്റ്റോഗ്രഫി എന്നിവയിൽ ഇത് വ്യാപകമായി ഉപയോഗിക്കുന്നു.
ASN.1: ക്രോസ്-പ്ലാറ്റ്ഫോം രീതിയിൽ സീരിയലൈസ് ചെയ്യാനും ഡിസീരിയലൈസ് ചെയ്യാനും കഴിയുന്ന ഡാറ്റാ ഘടനകളെ നിർവചിക്കുന്നതിനുള്ള ഒരു സ്റ്റാൻഡേർഡ് ഇന്റർഫേസ് വിവരണ ഭാഷയാണ് അമൂർത്ത സിന്റാക്സ് നൊട്ടേഷൻ വൺ ( ASN.1 ). ടെലികമ്മ്യൂണിക്കേഷൻ, കമ്പ്യൂട്ടർ നെറ്റ്‌വർക്കിംഗ്, പ്രത്യേകിച്ച് ക്രിപ്റ്റോഗ്രഫി എന്നിവയിൽ ഇത് വ്യാപകമായി ഉപയോഗിക്കുന്നു.
ASN.1: ക്രോസ്-പ്ലാറ്റ്ഫോം രീതിയിൽ സീരിയലൈസ് ചെയ്യാനും ഡിസീരിയലൈസ് ചെയ്യാനും കഴിയുന്ന ഡാറ്റാ ഘടനകളെ നിർവചിക്കുന്നതിനുള്ള ഒരു സ്റ്റാൻഡേർഡ് ഇന്റർഫേസ് വിവരണ ഭാഷയാണ് അമൂർത്ത സിന്റാക്സ് നൊട്ടേഷൻ വൺ ( ASN.1 ). ടെലികമ്മ്യൂണിക്കേഷൻ, കമ്പ്യൂട്ടർ നെറ്റ്‌വർക്കിംഗ്, പ്രത്യേകിച്ച് ക്രിപ്റ്റോഗ്രഫി എന്നിവയിൽ ഇത് വ്യാപകമായി ഉപയോഗിക്കുന്നു.
ASN.1: ക്രോസ്-പ്ലാറ്റ്ഫോം രീതിയിൽ സീരിയലൈസ് ചെയ്യാനും ഡിസീരിയലൈസ് ചെയ്യാനും കഴിയുന്ന ഡാറ്റാ ഘടനകളെ നിർവചിക്കുന്നതിനുള്ള ഒരു സ്റ്റാൻഡേർഡ് ഇന്റർഫേസ് വിവരണ ഭാഷയാണ് അമൂർത്ത സിന്റാക്സ് നൊട്ടേഷൻ വൺ ( ASN.1 ). ടെലികമ്മ്യൂണിക്കേഷൻ, കമ്പ്യൂട്ടർ നെറ്റ്‌വർക്കിംഗ്, പ്രത്യേകിച്ച് ക്രിപ്റ്റോഗ്രഫി എന്നിവയിൽ ഇത് വ്യാപകമായി ഉപയോഗിക്കുന്നു.
അമൂർത്ത വാക്യഘടന ട്രീ: കമ്പ്യൂട്ടർ സയൻസിൽ, ഒരു പ്രോഗ്രാമിംഗ് ഭാഷയിൽ എഴുതിയ സോഴ്‌സ് കോഡിന്റെ അമൂർത്ത വാക്യഘടനയുടെ ഒരു ട്രീ പ്രാതിനിധ്യമാണ് അമൂർത്ത സിന്റാക്സ് ട്രീ ( എഎസ്ടി ) അല്ലെങ്കിൽ സിന്റാക്സ് ട്രീ . ട്രീയുടെ ഓരോ നോഡും ഉറവിട കോഡിൽ സംഭവിക്കുന്ന ഒരു നിർമ്മാണത്തെ സൂചിപ്പിക്കുന്നു.
അമൂർത്ത സിദ്ധാന്തം: മുൻ അഞ്ച് അംഗം ആബ്സ് പുറത്തിറക്കിയ ആദ്യ സോളോ ആൽബമാണ് അബ്‌സ്ട്രാക്റ്റ് തിയറി . ഈ ആൽബം 2003 സെപ്റ്റംബർ 1 ന് പുറത്തിറങ്ങി, യുകെ ആൽബങ്ങളുടെ ചാർട്ടിൽ 29 ആം സ്ഥാനത്തെത്തി. മറ്റെവിടെയെങ്കിലും വിജയം കണ്ടെത്തുന്നതിൽ ഈ ആൽബം പരാജയപ്പെട്ടു, മാസങ്ങൾക്കുശേഷം അബ്സിനെ റെക്കോർഡ് ലേബലിൽ നിന്ന് ഒഴിവാക്കുകയും ചെയ്തു. "വാട്ട് യു ഗോറ്റ്", "സ്റ്റോപ്പ് സൈൻ", "ലജ്ജ", "7 വഴികൾ", "മിസ് പെർഫെക്റ്റ്" എന്നീ അഞ്ച് സിംഗിൾ‌സുകളാണ് ഈ ആൽബം സൃഷ്ടിച്ചത്. ഈ ആൽബം നിരൂപകരിൽ നിന്ന് നല്ല അവലോകനങ്ങൾ നേടി, അദ്ദേഹത്തിന്റെ മെറ്റീരിയലിനെ അദ്ദേഹത്തിന്റെ മുൻ ബാൻഡായ ഫൈവുമായി താരതമ്യപ്പെടുത്തി.
അമൂർത്തമായ പരുക്കൻ: കാലിഫോർണിയയിലെ ലോസ് ഏഞ്ചൽസിൽ നിന്നുള്ള റാപ്പറാണ് ആരോൺ പോയിന്റർ .
അമൂർത്തമായ സത്യം: 1969 ൽ ദക്ഷിണാഫ്രിക്കയിലെ ക്വാസുലു-നടാലിലെ ഡർബനിൽ രൂപീകരിച്ച ഒരു പുരോഗമന റോക്ക് ബാൻഡാണ് അബ്‌സ്ട്രാക്റ്റ് ട്രൂത്ത് . കോർ അംഗം കെൻ ഇ ഹെൻസണിനെ ചുറ്റിപ്പറ്റിയാണ് ബാൻഡ് രൂപീകരിച്ചത്.
അമൂർത്തമായ സത്യം: 1969 ൽ ദക്ഷിണാഫ്രിക്കയിലെ ക്വാസുലു-നടാലിലെ ഡർബനിൽ രൂപീകരിച്ച ഒരു പുരോഗമന റോക്ക് ബാൻഡാണ് അബ്‌സ്ട്രാക്റ്റ് ട്രൂത്ത് . കോർ അംഗം കെൻ ഇ ഹെൻസണിനെ ചുറ്റിപ്പറ്റിയാണ് ബാൻഡ് രൂപീകരിച്ചത്.
അമൂർത്ത വീനർ സ്പേസ്: അനന്ത-ഡൈമൻഷണൽ സ്പെയ്സുകളിലെ ഗ aus സിയൻ നടപടികളുടെ ഘടന മനസിലാക്കാൻ ലിയോനാർഡ് ഗ്രോസ് വികസിപ്പിച്ച ഗണിതശാസ്ത്ര നിർമ്മാണമാണ് അമൂർത്തമായ വീനർ സ്പേസ് എന്ന ആശയം. കാമറൂൺ-മാർട്ടിൻ സ്പേസ് വഹിക്കുന്ന അടിസ്ഥാന പങ്ക് നിർമാണത്തിന് emphas ന്നൽ നൽകുന്നു. ക്ലാസിക്കൽ വീനർ സ്പേസ് പ്രോട്ടോടൈപ്പിക്കൽ ഉദാഹരണമാണ്.
വിക്കി ഫംഗ്ഷനുകൾ: കോഡ് സൃഷ്ടിക്കുന്നതിനും പരിഷ്‌ക്കരിക്കുന്നതിനും പുനരുപയോഗിക്കുന്നതിനും അനുവദിക്കാൻ ലക്ഷ്യമിട്ടുള്ള ഫംഗ്ഷനുകളുടെ സഹകരണത്തോടെ എഡിറ്റുചെയ്‌ത കാറ്റലോഗാണ് വിക്കി ഫംഗ്ഷനുകൾ. ഇത് ഘടനാപരമായ ഡാറ്റ ഉപയോഗിച്ച് വിക്കിപീഡിയയുടെ ഭാഷ-സ്വതന്ത്ര പതിപ്പ് സൃഷ്ടിക്കാൻ ലക്ഷ്യമിടുന്ന വിക്കിഡാറ്റയിലേക്കുള്ള വിപുലീകരണമായ അബ്‌സ്ട്രാക്റ്റ് വിക്കിപീഡിയയുമായി അടുത്ത ബന്ധപ്പെട്ടിരിക്കുന്നു. പ്രാരംഭ പേരുകൾ താൽക്കാലികമായി കണക്കാക്കി; 2020 ഡിസംബർ 22 ന് വിക്കി ഫംഗ്ഷനുകളുടെ കൃത്യമായ പേര് പ്രഖ്യാപിച്ചു.
അമൂർത്ത വിൻഡോ ടൂൾകിറ്റ്: സ്വിംഗിനു മുമ്പുള്ള ജാവയുടെ യഥാർത്ഥ പ്ലാറ്റ്ഫോം-ആശ്രിത വിൻഡോസിംഗ്, ഗ്രാഫിക്സ്, ഉപയോക്തൃ-ഇന്റർഫേസ് വിജറ്റ് ടൂൾകിറ്റ് എന്നിവയാണ് അമൂർത്ത വിൻഡോ ടൂൾകിറ്റ് ( AWT ). ജാവ പ്രോഗ്രാമിനായി ഗ്രാഫിക്കൽ യൂസർ ഇന്റർഫേസ് (ജിയുഐ) നൽകുന്നതിനുള്ള സ്റ്റാൻഡേർഡ് എപിഐ ജാവ ഫ Foundation ണ്ടേഷൻ ക്ലാസുകളുടെ (ജെഎഫ്സി) ഭാഗമാണ് എഡബ്ല്യുടി. നിരവധി ജാവ എംഇ പ്രൊഫൈലുകൾക്കുള്ള ജിയുഐ ടൂൾകിറ്റ് കൂടിയാണ് എഡബ്ല്യുടി. ഉദാഹരണത്തിന്, ബന്ധിപ്പിച്ച ഉപകരണ കോൺഫിഗറേഷൻ പ്രൊഫൈലുകൾക്ക് മൊബൈൽ ടെലിഫോണുകളിൽ ജാവാ റൺടൈമുകൾ അമൂർത്ത വിൻഡോ ടൂൾകിറ്റിനെ പിന്തുണയ്‌ക്കാൻ ആവശ്യമാണ്.
അമൂർത്ത വിൻഡോ ടൂൾകിറ്റ്: സ്വിംഗിനു മുമ്പുള്ള ജാവയുടെ യഥാർത്ഥ പ്ലാറ്റ്ഫോം-ആശ്രിത വിൻഡോസിംഗ്, ഗ്രാഫിക്സ്, ഉപയോക്തൃ-ഇന്റർഫേസ് വിജറ്റ് ടൂൾകിറ്റ് എന്നിവയാണ് അമൂർത്ത വിൻഡോ ടൂൾകിറ്റ് ( AWT ). ജാവ പ്രോഗ്രാമിനായി ഗ്രാഫിക്കൽ യൂസർ ഇന്റർഫേസ് (ജിയുഐ) നൽകുന്നതിനുള്ള സ്റ്റാൻഡേർഡ് എപിഐ ജാവ ഫ Foundation ണ്ടേഷൻ ക്ലാസുകളുടെ (ജെഎഫ്സി) ഭാഗമാണ് എഡബ്ല്യുടി. നിരവധി ജാവ എംഇ പ്രൊഫൈലുകൾക്കുള്ള ജിയുഐ ടൂൾകിറ്റ് കൂടിയാണ് എഡബ്ല്യുടി. ഉദാഹരണത്തിന്, ബന്ധിപ്പിച്ച ഉപകരണ കോൺഫിഗറേഷൻ പ്രൊഫൈലുകൾക്ക് മൊബൈൽ ടെലിഫോണുകളിൽ ജാവാ റൺടൈമുകൾ അമൂർത്ത വിൻഡോ ടൂൾകിറ്റിനെ പിന്തുണയ്‌ക്കാൻ ആവശ്യമാണ്.
സയണിസം: ചരിത്രപരമായ ഇസ്രായേൽ ഭൂമി എന്ന് നിർവചിക്കപ്പെട്ടിട്ടുള്ള പ്രദേശത്ത് ഒരു ജൂത രാഷ്ട്രത്തെ പുന -സ്ഥാപിക്കുന്നതിനും പിന്തുണയ്ക്കുന്നതിനും സഹായിക്കുന്ന ഒരു പ്രത്യയശാസ്ത്രവും ദേശീയ പ്രസ്ഥാനവുമാണ് സയണിസം . പത്തൊൻപതാം നൂറ്റാണ്ടിന്റെ അവസാനത്തിൽ മധ്യ-കിഴക്കൻ യൂറോപ്പിൽ ഒരു ദേശീയ പുനരുജ്ജീവന പ്രസ്ഥാനമായി ആധുനിക സയണിസം ഉയർന്നുവന്നു, ഇത് പുതിയ ആന്റിസെമിറ്റിസം തരംഗങ്ങളോടുള്ള പ്രതികരണമായും ഹസ്‌കലയോടോ യഹൂദ പ്രബുദ്ധതയിലോ ഉള്ള പ്രതികരണമായി. ഇതിനു തൊട്ടുപിന്നാലെ, പ്രസ്ഥാനത്തിന്റെ ഭൂരിഭാഗം നേതാക്കളും പ്രധാന ലക്ഷ്യത്തെ പലസ്തീനിൽ ആവശ്യമുള്ള സംസ്ഥാനം സൃഷ്ടിക്കുന്നതുമായി ബന്ധപ്പെടുത്തി, തുടർന്ന് ഓട്ടോമൻ സാമ്രാജ്യത്തിന്റെ നിയന്ത്രണത്തിലുള്ള പ്രദേശമായിരുന്നു.
അമൂർത്ത അഡിറ്റീവ് ഷ്വാർസ് രീതി: ഗണിതശാസ്ത്രം, ഹെർമൻ Schwarz പേരിലാണ് അമൂർത്തമായ അധിക Schwarz രീതി,, ഭാഗിക ഡിഫറൻഷ്യൽ സമവാക്യങ്ങളുടെ അതിർത്തി മൂല്യം പ്രശ്നങ്ങൾ, ഡൊമെയ്നുകളുടെ റഫറൻസ് ഇല്ലാതെ ലീനിയർ ആൽജിബ്രാ കണക്കിലെടുത്ത് രൂപം വേണ്ടി അധിക Schwarz രീതി ഒരു സംഗ്രഹവും പതിപ്പാണ്, ഉപഡൊമെയ്നുകൾ, മുതലായവ പല എങ്കിൽ എല്ലാ ഡൊമെയ്ൻ വിഘടിപ്പിക്കൽ രീതികളും അമൂർത്ത അഡിറ്റീവ് ഷ്വാർസ് രീതിയായി കാസ്റ്റുചെയ്യാൻ കഴിയില്ല, ഇത് പലപ്പോഴും അവരുടെ വിശകലനത്തിനുള്ള ആദ്യത്തേതും ഏറ്റവും സൗകര്യപ്രദവുമായ സമീപനമാണ്.
അമൂർത്ത അഡിറ്റീവ് ഷ്വാർസ് രീതി: ഗണിതശാസ്ത്രം, ഹെർമൻ Schwarz പേരിലാണ് അമൂർത്തമായ അധിക Schwarz രീതി,, ഭാഗിക ഡിഫറൻഷ്യൽ സമവാക്യങ്ങളുടെ അതിർത്തി മൂല്യം പ്രശ്നങ്ങൾ, ഡൊമെയ്നുകളുടെ റഫറൻസ് ഇല്ലാതെ ലീനിയർ ആൽജിബ്രാ കണക്കിലെടുത്ത് രൂപം വേണ്ടി അധിക Schwarz രീതി ഒരു സംഗ്രഹവും പതിപ്പാണ്, ഉപഡൊമെയ്നുകൾ, മുതലായവ പല എങ്കിൽ എല്ലാ ഡൊമെയ്ൻ വിഘടിപ്പിക്കൽ രീതികളും അമൂർത്ത അഡിറ്റീവ് ഷ്വാർസ് രീതിയായി കാസ്റ്റുചെയ്യാൻ കഴിയില്ല, ഇത് പലപ്പോഴും അവരുടെ വിശകലനത്തിനുള്ള ആദ്യത്തേതും ഏറ്റവും സൗകര്യപ്രദവുമായ സമീപനമാണ്.
അമൂർത്ത ബീജഗണിതം: ഗണിതശാസ്ത്രത്തിന്റെ വിശാലമായ വിഭജനമായ ബീജഗണിതത്തിൽ , ബീജഗണിത ഘടനകളെക്കുറിച്ചുള്ള പഠനമാണ് അമൂർത്ത ബീജഗണിതം . ബീജഗണിത ഘടനയിൽ ഗ്രൂപ്പുകൾ, വളയങ്ങൾ, ഫീൽഡുകൾ, മൊഡ്യൂളുകൾ, വെക്റ്റർ ഇടങ്ങൾ, ലാറ്റിസുകൾ, ബീജഗണിതങ്ങൾ എന്നിവ ഉൾപ്പെടുന്നു. ബീജഗണിതത്തിന്റെ മറ്റ് ഭാഗങ്ങളിൽ നിന്ന് ഈ പഠന മേഖലയെ വേർതിരിച്ചറിയാൻ ഇരുപതാം നൂറ്റാണ്ടിന്റെ തുടക്കത്തിൽ അമൂർത്ത ബീജഗണിതം എന്ന പദം ഉപയോഗിച്ചു.
ലെബ്നിസ് ഓപ്പറേറ്റർ: ഗണിതശാസ്ത്ര യുക്തിയുടെ ഒരു ശാഖയായ അമൂർത്ത ബീജഗണിത യുക്തിയിൽ, കൃത്യമായ സാങ്കേതിക നിർവചനമുള്ളതും ധാരാളം ലോജിക്കുകൾ പിടിച്ചെടുക്കുന്നതുമായ കിഴിവ് സംവിധാനങ്ങളെ തരംതിരിക്കാനുള്ള ഉപകരണമാണ് ലീബ്നിസ് ഓപ്പറേറ്റർ . ഈ മേഖലയുടെ സ്ഥാപകരിൽ രണ്ടുപേരായ വിം ബ്ലോക്കും ഡോൺ പിഗോസിയും ചേർന്നാണ് ലെബ്നിസ് ഓപ്പറേറ്റർ അവതരിപ്പിച്ചത്, അറിയപ്പെടുന്ന ലിൻഡെൻബാം-ടാർസ്കി പ്രക്രിയയെ സംഗ്രഹിക്കുന്നതിനുള്ള ഒരു മാർഗമായി, ഇത് ബൂലിയൻ ആൾജിബ്രകളെ ക്ലാസിക്കൽ പ്രൊപ്പോസിഷണൽ കാൽക്കുലസുമായി ബന്ധപ്പെടുത്തുന്നതിലേക്ക് നയിക്കുന്നു, കഴിയുന്നത്ര വൈവിധ്യമാർന്ന അയയ്‌ക്കൽ ലോജിക്കുകൾക്ക് ബാധകമാണ്. തന്നിരിക്കുന്ന സെൻഡൻഷ്യൽ ലോജിക്കിന്റെ തന്നിരിക്കുന്ന ഒരു സിദ്ധാന്തത്തിലേക്ക് നിയോഗിക്കുന്ന ഒരു ഓപ്പറേറ്ററാണ് ഇത്, ഒരു സ്വതന്ത്ര ബീജഗണിതമായി അതിന്റെ പ്രപഞ്ചത്തിൽ ഒരു പരിണതഫലമായി പ്രവർത്തിക്കുന്നു, ഇത് ബീജഗണിതത്തിലെ ഏറ്റവും വലിയ സാമാന്യതയാണ്.
അമൂർത്ത ബീജഗണിത യുക്തി: ഗണിതശാസ്ത്രപരമായ യുക്തിയിൽ, അറിയപ്പെടുന്ന ലിൻഡെൻബാം-ടാർസ്കി ബീജഗണിതത്തിന്റെ ഒരു സംഗ്രഹമായി കിഴിവ് വ്യവസ്ഥകളുടെ ബീജഗണിതവൽക്കരണത്തെക്കുറിച്ചും അതിന്റെ ഫലമായുണ്ടാകുന്ന ബീജഗണിതങ്ങൾ ലോജിക്കൽ സിസ്റ്റങ്ങളുമായി എങ്ങനെ ബന്ധപ്പെട്ടിരിക്കുന്നുവെന്നും പഠിക്കുന്നതാണ് അമൂർത്ത ബീജഗണിത യുക്തി .
ബീജഗണിത ഇനം: ഗണിതശാസ്ത്രത്തിന്റെ ഉപമേഖലയായ ബീജഗണിത ജ്യാമിതിയിലെ പഠനത്തിന്റെ കേന്ദ്ര വസ്‌തുക്കളാണ് ബീജഗണിത ഇനങ്ങൾ . ക്ലാസിക്കലായി, ഒരു ബീജഗണിത വൈവിധ്യത്തെ യഥാർത്ഥ അല്ലെങ്കിൽ സങ്കീർണ്ണ സംഖ്യകളെക്കാൾ പോളിനോമിയൽ സമവാക്യങ്ങളുടെ പരിഹാരങ്ങളുടെ കൂട്ടമായി നിർവചിച്ചിരിക്കുന്നു. യഥാർത്ഥ നിർവചനത്തിന് പിന്നിലുള്ള ജ്യാമിതീയ അവബോധം സംരക്ഷിക്കാൻ ശ്രമിക്കുമ്പോൾ ആധുനിക നിർവചനങ്ങൾ ഈ ആശയത്തെ പലവിധത്തിൽ സാമാന്യവൽക്കരിക്കുന്നു.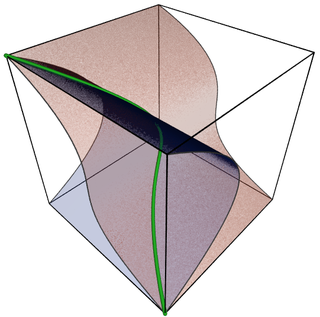
അമൂർത്ത ബീജഗണിതം: ഗണിതശാസ്ത്രത്തിന്റെ വിശാലമായ വിഭജനമായ ബീജഗണിതത്തിൽ , ബീജഗണിത ഘടനകളെക്കുറിച്ചുള്ള പഠനമാണ് അമൂർത്ത ബീജഗണിതം . ബീജഗണിത ഘടനയിൽ ഗ്രൂപ്പുകൾ, വളയങ്ങൾ, ഫീൽഡുകൾ, മൊഡ്യൂളുകൾ, വെക്റ്റർ ഇടങ്ങൾ, ലാറ്റിസുകൾ, ബീജഗണിതങ്ങൾ എന്നിവ ഉൾപ്പെടുന്നു. ബീജഗണിതത്തിന്റെ മറ്റ് ഭാഗങ്ങളിൽ നിന്ന് ഈ പഠന മേഖലയെ വേർതിരിച്ചറിയാൻ ഇരുപതാം നൂറ്റാണ്ടിന്റെ തുടക്കത്തിൽ അമൂർത്ത ബീജഗണിതം എന്ന പദം ഉപയോഗിച്ചു.
വിശകലന പ്രവർത്തനം: ഗണിതശാസ്ത്രത്തിൽ, ഒരു സംയോജിത പവർ സീരീസ് പ്രാദേശികമായി നൽകുന്ന ഒരു ഫംഗ്ഷനാണ് അനലിറ്റിക് ഫംഗ്ഷൻ . യഥാർത്ഥ വിശകലന പ്രവർത്തനങ്ങളും സങ്കീർണ്ണമായ വിശകലന പ്രവർത്തനങ്ങളും നിലവിലുണ്ട്. ഓരോ തരത്തിലുമുള്ള പ്രവർത്തനങ്ങൾ അനന്തമായി വ്യത്യാസപ്പെട്ടിരിക്കുന്നു, പക്ഷേ സങ്കീർണ്ണമായ വിശകലന പ്രവർത്തനങ്ങൾ യഥാർത്ഥ അനലിറ്റിക് ഫംഗ്ഷനുകൾക്ക് പൊതുവെ കൈവശം വയ്ക്കാത്ത സവിശേഷതകൾ പ്രദർശിപ്പിക്കുന്നു. X 0 നെക്കുറിച്ചുള്ള ടെയ്‌ലർ സീരീസ് അതിന്റെ ഡൊമെയ്‌നിലെ ഓരോ x 0 നും ചില സമീപസ്ഥലങ്ങളിലെ ഫംഗ്ഷനിലേക്ക് സംയോജിക്കുന്നുവെങ്കിൽ മാത്രമേ ഒരു ഫംഗ്ഷൻ വിശകലനം ചെയ്യൂ.
അമൂർത്ത വിശകലന സംഖ്യ സിദ്ധാന്തം: ക്ലാസിക്കൽ അനലിറ്റിക് നമ്പർ സിദ്ധാന്തത്തിന്റെ ആശയങ്ങളും സാങ്കേതികതകളും എടുത്ത് വിവിധ ഗണിതശാസ്ത്ര മേഖലകളിൽ പ്രയോഗിക്കുന്ന ഗണിതശാസ്ത്രത്തിന്റെ ഒരു ശാഖയാണ് അമൂർത്ത അനലിറ്റിക് നമ്പർ സിദ്ധാന്തം . ക്ലാസിക്കൽ പ്രൈം നമ്പർ സിദ്ധാന്തം ഒരു പ്രോട്ടോടൈപ്പിക്കൽ ഉദാഹരണമായി വർത്തിക്കുന്നു, കൂടാതെ അമൂർത്ത അസിംപ്റ്റോട്ടിക് വിതരണ ഫലങ്ങൾക്ക് is ന്നൽ നൽകുന്നു. ഇരുപതാം നൂറ്റാണ്ടിൽ ഗണിതശാസ്ത്രജ്ഞന്മാരായ ജോൺ നോപ്മാക്കർ, ആർനെ ബർലിംഗ് എന്നിവർ ഈ സിദ്ധാന്തം കണ്ടുപിടിക്കുകയും വികസിപ്പിക്കുകയും ചെയ്തു.
അമൂർത്തവും പ്രായോഗികവുമായ വിശകലനം: അമൂർത്തവും പ്രായോഗികവുമായ വിശകലന മേഖലകളും ലീനിയർ, നോൺ-ലീനിയർ സാധാരണ, ഭാഗിക ഡിഫറൻഷ്യൽ സമവാക്യങ്ങൾ, ഒപ്റ്റിമൈസേഷൻ സിദ്ധാന്തം, നിയന്ത്രണ സിദ്ധാന്തം എന്നിവപോലുള്ള പരമ്പരാഗത വിശകലന രീതികളും ഉൾക്കൊള്ളുന്ന ഒരു പിയർ അവലോകനം ചെയ്ത ഗണിതശാസ്ത്ര ജേണലാണ് അബ്‌സ്ട്രാക്റ്റ് ആൻഡ് അപ്ലൈഡ് അനാലിസിസ് . ഹിന്ദാവി പബ്ലിഷിംഗ് കോർപ്പറേഷനാണ് ഇത് പ്രസിദ്ധീകരിക്കുന്നത്. 2005 വരെ എഡിറ്റർ‌-ഇൻ-ചീഫ് ആയിരുന്ന 1996 ൽ അത്തനാസിയോസ് ജി. -ഇൻ-ചീഫ്, എഡിറ്റോറിയൽ ബോർഡ് അംഗങ്ങൾ എടുത്ത എഡിറ്റോറിയൽ തീരുമാനങ്ങളുമായി. അപാകത ഉദ്ധരണി പാറ്റേണുകൾക്കായി ജേണൽ സൈറ്റേഷൻ റിപ്പോർട്ടുകളിൽ നിന്ന് ഒഴിവാക്കുന്നത് ജേണൽ നേരിട്ടു.
അമൂർത്തവും പ്രായോഗികവുമായ വിശകലനം: അമൂർത്തവും പ്രായോഗികവുമായ വിശകലന മേഖലകളും ലീനിയർ, നോൺ-ലീനിയർ സാധാരണ, ഭാഗിക ഡിഫറൻഷ്യൽ സമവാക്യങ്ങൾ, ഒപ്റ്റിമൈസേഷൻ സിദ്ധാന്തം, നിയന്ത്രണ സിദ്ധാന്തം എന്നിവപോലുള്ള പരമ്പരാഗത വിശകലന രീതികളും ഉൾക്കൊള്ളുന്ന ഒരു പിയർ അവലോകനം ചെയ്ത ഗണിതശാസ്ത്ര ജേണലാണ് അബ്‌സ്ട്രാക്റ്റ് ആൻഡ് അപ്ലൈഡ് അനാലിസിസ് . ഹിന്ദാവി പബ്ലിഷിംഗ് കോർപ്പറേഷനാണ് ഇത് പ്രസിദ്ധീകരിക്കുന്നത്. 2005 വരെ എഡിറ്റർ‌-ഇൻ-ചീഫ് ആയിരുന്ന 1996 ൽ അത്തനാസിയോസ് ജി. -ഇൻ-ചീഫ്, എഡിറ്റോറിയൽ ബോർഡ് അംഗങ്ങൾ എടുത്ത എഡിറ്റോറിയൽ തീരുമാനങ്ങളുമായി. അപാകത ഉദ്ധരണി പാറ്റേണുകൾക്കായി ജേണൽ സൈറ്റേഷൻ റിപ്പോർട്ടുകളിൽ നിന്ന് ഒഴിവാക്കുന്നത് ജേണൽ നേരിട്ടു.
അവലംബ സൂചിക: ഒരു ഉദ്ധരണി സൂചിക എന്നത് ഒരുതരം ഗ്രന്ഥസൂചിക സൂചികയാണ്, പ്രസിദ്ധീകരണങ്ങൾ തമ്മിലുള്ള അവലംബങ്ങളുടെ സൂചികയാണ്, മുമ്പത്തെ ഏത് രേഖകളാണ് ഉദ്ധരിക്കുന്നതെന്ന് പിന്നീട് സ്ഥാപിക്കാൻ ഉപയോക്താവിനെ അനുവദിക്കുന്നു. പന്ത്രണ്ടാം നൂറ്റാണ്ടിലെ എബ്രായ മതസാഹിത്യത്തിലാണ് ഉദ്ധരണി സൂചികയുടെ ഒരു രൂപം ആദ്യമായി കണ്ടെത്തിയത്. പതിനെട്ടാം നൂറ്റാണ്ടിൽ നിയമപരമായ അവലംബ സൂചികകൾ കണ്ടെത്തിയിട്ടുണ്ട്, അവ ഷെപ്പേർഡ്സ് സൈറ്റേഷൻസ് (1873) പോലുള്ള സൈറ്റേറ്റർമാർ ജനപ്രിയമാക്കി. 1960-ൽ യൂജിൻ ഗാർഫീൽഡിന്റെ ഇൻസ്റ്റിറ്റ്യൂട്ട് ഫോർ സയന്റിഫിക് ഇൻഫർമേഷൻ (ഐ.എസ്.ഐ) അക്കാദമിക് ജേണലുകളിൽ പ്രസിദ്ധീകരിച്ച പ്രബന്ധങ്ങൾക്കായുള്ള ആദ്യത്തെ അവലംബ സൂചിക അവതരിപ്പിച്ചു, ആദ്യം സയൻസ് സൈറ്റേഷൻ ഇൻഡെക്സ് (എസ്‌സി‌ഐ), പിന്നീട് സോഷ്യൽ സയൻസസ് സൈറ്റേഷൻ ഇൻഡെക്സ് (എസ്എസ്സിഐ), ആർട്സ് ആൻഡ് ഹ്യൂമാനിറ്റീസ് സൈറ്റേഷൻ ഇൻഡെക്സ് (AHCI). ആദ്യത്തെ ഓട്ടോമേറ്റഡ് സൈറ്റേഷൻ ഇൻഡെക്സിംഗ് 1997 ൽ സൈറ്റ്സീർ ചെയ്തു, പേറ്റന്റ് നേടി. അത്തരം ഡാറ്റയുടെ മറ്റ് ഉറവിടങ്ങളിൽ Google സ്കോളർ, എൽസെവിയേഴ്സ് സ്കോപ്പസ് എന്നിവ ഉൾപ്പെടുന്നു.
അമൂർത്തവും കോൺക്രീറ്റും: മെറ്റാഫിസിക്‌സിൽ, അമൂർത്തവും കോൺക്രീറ്റും തമ്മിലുള്ള വ്യത്യാസം രണ്ട് തരം എന്റിറ്റികൾ തമ്മിലുള്ള വിഭജനത്തെ സൂചിപ്പിക്കുന്നു. ഈ വ്യത്യാസത്തിന് അടിസ്ഥാന മെറ്റാഫിസിക്കൽ പ്രാധാന്യമുണ്ടെന്ന് പല തത്ത്വചിന്തകരും അഭിപ്രായപ്പെടുന്നു. കോൺക്രീറ്റ് വസ്തുക്കളുടെ ഉദാഹരണങ്ങളിൽ സസ്യങ്ങൾ, മനുഷ്യർ, ഗ്രഹങ്ങൾ എന്നിവ ഉൾപ്പെടുന്നു, അതേസമയം സംഖ്യകൾ, സെറ്റുകൾ, നിർദ്ദേശങ്ങൾ എന്നിവ അമൂർത്ത വസ്തുക്കളാണ് . ദൃ ret തയുടെയും അമൂർത്തതയുടെയും സ്വഭാവ ചിഹ്നങ്ങൾ എന്താണെന്നതിന് പൊതുവായ അഭിപ്രായ സമന്വയമില്ല. (1) സ്ഥല-സമയത്തിനകത്തോ പുറത്തോ ഉള്ള അസ്തിത്വം, (2) കാരണങ്ങളും ഫലങ്ങളും ഉണ്ടോ ഇല്ലയോ, (3) അനിശ്ചിതത്വത്തിലോ ആവശ്യമുള്ളതോ ഉള്ള അസ്തിത്വം, (4) പ്രത്യേകമോ സാർവത്രികമോ (5) ശാരീരികമോ മാനസികമോ ആയ മേഖലയിലോ അല്ലാതെയോ. ഈ വൈവിധ്യമാർന്ന കാഴ്ചപ്പാടുകൾ ഉണ്ടായിരുന്നിട്ടും, മിക്ക വസ്തുക്കളും അമൂർത്തമോ കോൺക്രീറ്റോ ആണോ എന്നതിനെക്കുറിച്ച് വിശാലമായ ധാരണയുണ്ട്. അതിനാൽ മിക്ക വ്യാഖ്യാനങ്ങളിലും, ഈ കാഴ്ചപ്പാടുകളെല്ലാം സമ്മതിക്കും, ഉദാഹരണത്തിന്, സസ്യങ്ങൾ കോൺക്രീറ്റ് വസ്തുക്കളാണ്, അക്കങ്ങൾ അമൂർത്ത വസ്തുക്കളാണ്.
നോൺ-നോറേറ്റീവ് ഫിലിം: നോൺ-നോറേറ്റീവ് ഫിലിം സിനിമാറ്റിക് ഫിലിമിന്റെ സൗന്ദര്യാത്മകമാണ്, അത് "ഒരു സംഭവത്തെ യഥാർത്ഥമോ സാങ്കൽപ്പികമോ" എന്ന് വിവരിക്കുകയോ വിവരിക്കുകയോ ഇല്ല. ഇത് സാധാരണയായി ഒരു കലാ ചലച്ചിത്രത്തിന്റെ അല്ലെങ്കിൽ പരീക്ഷണാത്മക സിനിമയാണ്, ഇത് പൊതു വിനോദത്തിനായി നിർമ്മിച്ചിട്ടില്ല.
അപീറോജോൺ: ജ്യാമിതിയിൽ, എണ്ണമറ്റ അനന്തമായ വശങ്ങളുള്ള ഒരു സാമാന്യവൽക്കരിച്ച പോളിഗോണാണ് അപീറോൺ അല്ലെങ്കിൽ അനന്തമായ പോളിഗോൺ . അനന്തമായ പോളിറ്റോപ്പുകളുടെ ദ്വിമാന കേസാണ് അപീറോഗോണുകൾ.
അപീറോടോപ്പ്: അനന്തമായ നിരവധി വശങ്ങളുള്ള ഒരു സാമാന്യവൽക്കരിച്ച പോളിറ്റോപ്പാണ് അപീറോടോപ്പ് അല്ലെങ്കിൽ അനന്തമായ പോളിറ്റോപ്പ് .
അമൂർത്ത കല: ലോകത്തിലെ വിഷ്വൽ റഫറൻസുകളിൽ നിന്ന് ഒരു പരിധിവരെ സ്വാതന്ത്ര്യത്തോടുകൂടിയ ഒരു രചന സൃഷ്ടിക്കാൻ അമൂർത്ത കല രൂപം, രൂപം, നിറം, രേഖ എന്നിവയുടെ വിഷ്വൽ ഭാഷ ഉപയോഗിക്കുന്നു. പാശ്ചാത്യ കല, നവോത്ഥാനം മുതൽ പത്തൊൻപതാം നൂറ്റാണ്ടിന്റെ മദ്ധ്യകാലം വരെ, കാഴ്ചപ്പാടിന്റെ യുക്തിയും ദൃശ്യമായ യാഥാർത്ഥ്യത്തിന്റെ ഒരു മിഥ്യാധാരണയെ പുനർനിർമ്മിക്കാനുള്ള ശ്രമവുമാണ്. പത്തൊൻപതാം നൂറ്റാണ്ടിന്റെ അവസാനത്തോടെ സാങ്കേതികവിദ്യ, ശാസ്ത്രം, തത്ത്വചിന്ത എന്നിവയിൽ സംഭവിക്കുന്ന അടിസ്ഥാനപരമായ മാറ്റങ്ങൾ ഉൾക്കൊള്ളുന്ന ഒരു പുതിയ തരം കല സൃഷ്ടിക്കേണ്ടതുണ്ടെന്ന് പല കലാകാരന്മാർക്കും തോന്നി. വ്യക്തിഗത കലാകാരന്മാർ അവരുടെ സൈദ്ധാന്തിക വാദങ്ങൾ ഉന്നയിച്ച ഉറവിടങ്ങൾ വൈവിധ്യപൂർണ്ണമായിരുന്നു, അക്കാലത്ത് പാശ്ചാത്യ സംസ്കാരത്തിന്റെ എല്ലാ മേഖലകളിലെയും സാമൂഹികവും ബ ual ദ്ധികവുമായ മുൻ‌തൂക്കങ്ങൾ പ്രതിഫലിപ്പിച്ചു.
അമൂർത്ത കല: ലോകത്തിലെ വിഷ്വൽ റഫറൻസുകളിൽ നിന്ന് ഒരു പരിധിവരെ സ്വാതന്ത്ര്യത്തോടുകൂടിയ ഒരു രചന സൃഷ്ടിക്കാൻ അമൂർത്ത കല രൂപം, രൂപം, നിറം, രേഖ എന്നിവയുടെ വിഷ്വൽ ഭാഷ ഉപയോഗിക്കുന്നു. പാശ്ചാത്യ കല, നവോത്ഥാനം മുതൽ പത്തൊൻപതാം നൂറ്റാണ്ടിന്റെ മദ്ധ്യകാലം വരെ, കാഴ്ചപ്പാടിന്റെ യുക്തിയും ദൃശ്യമായ യാഥാർത്ഥ്യത്തിന്റെ ഒരു മിഥ്യാധാരണയെ പുനർനിർമ്മിക്കാനുള്ള ശ്രമവുമാണ്. പത്തൊൻപതാം നൂറ്റാണ്ടിന്റെ അവസാനത്തോടെ സാങ്കേതികവിദ്യ, ശാസ്ത്രം, തത്ത്വചിന്ത എന്നിവയിൽ സംഭവിക്കുന്ന അടിസ്ഥാനപരമായ മാറ്റങ്ങൾ ഉൾക്കൊള്ളുന്ന ഒരു പുതിയ തരം കല സൃഷ്ടിക്കേണ്ടതുണ്ടെന്ന് പല കലാകാരന്മാർക്കും തോന്നി. വ്യക്തിഗത കലാകാരന്മാർ അവരുടെ സൈദ്ധാന്തിക വാദങ്ങൾ ഉന്നയിച്ച ഉറവിടങ്ങൾ വൈവിധ്യപൂർണ്ണമായിരുന്നു, അക്കാലത്ത് പാശ്ചാത്യ സംസ്കാരത്തിന്റെ എല്ലാ മേഖലകളിലെയും സാമൂഹികവും ബ ual ദ്ധികവുമായ മുൻ‌തൂക്കങ്ങൾ പ്രതിഫലിപ്പിച്ചു.
അമൂർത്ത കല: ലോകത്തിലെ വിഷ്വൽ റഫറൻസുകളിൽ നിന്ന് ഒരു പരിധിവരെ സ്വാതന്ത്ര്യത്തോടുകൂടിയ ഒരു രചന സൃഷ്ടിക്കാൻ അമൂർത്ത കല രൂപം, രൂപം, നിറം, രേഖ എന്നിവയുടെ വിഷ്വൽ ഭാഷ ഉപയോഗിക്കുന്നു. പാശ്ചാത്യ കല, നവോത്ഥാനം മുതൽ പത്തൊൻപതാം നൂറ്റാണ്ടിന്റെ മദ്ധ്യകാലം വരെ, കാഴ്ചപ്പാടിന്റെ യുക്തിയും ദൃശ്യമായ യാഥാർത്ഥ്യത്തിന്റെ ഒരു മിഥ്യാധാരണയെ പുനർനിർമ്മിക്കാനുള്ള ശ്രമവുമാണ്. പത്തൊൻപതാം നൂറ്റാണ്ടിന്റെ അവസാനത്തോടെ സാങ്കേതികവിദ്യ, ശാസ്ത്രം, തത്ത്വചിന്ത എന്നിവയിൽ സംഭവിക്കുന്ന അടിസ്ഥാനപരമായ മാറ്റങ്ങൾ ഉൾക്കൊള്ളുന്ന ഒരു പുതിയ തരം കല സൃഷ്ടിക്കേണ്ടതുണ്ടെന്ന് പല കലാകാരന്മാർക്കും തോന്നി. വ്യക്തിഗത കലാകാരന്മാർ അവരുടെ സൈദ്ധാന്തിക വാദങ്ങൾ ഉന്നയിച്ച ഉറവിടങ്ങൾ വൈവിധ്യപൂർണ്ണമായിരുന്നു, അക്കാലത്ത് പാശ്ചാത്യ സംസ്കാരത്തിന്റെ എല്ലാ മേഖലകളിലെയും സാമൂഹികവും ബ ual ദ്ധികവുമായ മുൻ‌തൂക്കങ്ങൾ പ്രതിഫലിപ്പിച്ചു.
പ്രോപ്പർട്ടി (തത്ത്വചിന്ത): യുക്തിയിലും തത്ത്വചിന്തയിലും ഒരു സ്വത്ത് ഒരു വസ്തുവിന്റെ സ്വഭാവമാണ്; ഒരു ചുവന്ന വസ്തുവിന് ചുവപ്പിന്റെ സ്വത്ത് ഉണ്ടെന്ന് പറയപ്പെടുന്നു. പ്രോപ്പർട്ടി സ്വന്തമായി ഒരു വസ്തുവിന്റെ രൂപമായി കണക്കാക്കാം, മറ്റ് സ്വത്തുക്കൾ കൈവശം വയ്ക്കാൻ കഴിയും. എന്നിരുന്നാലും, ഒരു സ്വത്ത് വ്യക്തിഗത വസ്‌തുക്കളിൽ നിന്ന് വ്യത്യസ്‌തമാണ്, അത് തൽക്ഷണം ചെയ്യപ്പെടാം, പലപ്പോഴും ഒന്നിലധികം കാര്യങ്ങളിൽ. ക്ലാസ്സിന്റെ ലോജിക്കൽ / മാത്തമാറ്റിക്കൽ സങ്കൽപ്പത്തിൽ നിന്ന് എക്സ്റ്റെൻഷണാലിറ്റി എന്ന ആശയം ഇല്ലാത്തതിനാൽ ഇത് വ്യത്യാസപ്പെട്ടിരിക്കുന്നു, കൂടാതെ ക്ലാസ് എന്ന ദാർശനിക സങ്കൽപ്പത്തിൽ നിന്ന് ഒരു സ്വത്ത് കൈവശമുള്ള വസ്തുക്കളിൽ നിന്ന് വ്യത്യസ്തമാണെന്ന് കണക്കാക്കപ്പെടുന്നു. വ്യത്യസ്‌ത വ്യക്തിഗത എന്റിറ്റികൾക്ക് ചില അർത്ഥത്തിൽ സമാനമായ ചില സ്വഭാവങ്ങൾ എങ്ങനെ ഉണ്ടെന്ന് മനസ്സിലാക്കുന്നത് സാർവത്രിക പ്രശ്‌നത്തിന്റെ അടിസ്ഥാനമാണ്.
സംഗ്രഹം: നിർദ്ദിഷ്ട ഉദാഹരണങ്ങൾ, അക്ഷര സൂചകങ്ങൾ, ആദ്യ തത്ത്വങ്ങൾ അല്ലെങ്കിൽ മറ്റ് രീതികളുടെ ഉപയോഗത്തിൽ നിന്നും വർഗ്ഗീകരണത്തിൽ നിന്നും പൊതുവായ നിയമങ്ങളും ആശയങ്ങളും ഉരുത്തിരിഞ്ഞ ഒരു ആശയപരമായ പ്രക്രിയയാണ് അതിന്റെ പ്രധാന അർത്ഥത്തിൽ അമൂർത്തീകരണം .
ക്ലാസ് (കമ്പ്യൂട്ടർ പ്രോഗ്രാമിംഗ്): ഒബ്ജക്റ്റ്-ഓറിയന്റഡ് പ്രോഗ്രാമിംഗിൽ, ഒബ്ജക്റ്റുകൾ സൃഷ്ടിക്കുന്നതിനും സംസ്ഥാനത്തിന് പ്രാരംഭ മൂല്യങ്ങൾ നൽകുന്നതിനും പെരുമാറ്റത്തിന്റെ നടപ്പാക്കലിനുമുള്ള വിപുലീകരിക്കാവുന്ന പ്രോഗ്രാം-കോഡ്-ടെംപ്ലേറ്റാണ് ക്ലാസ് . പല ഭാഷകളിലും, ക്ലാസ് നാമം ക്ലാസിന്റെ പേരായും ക്ലാസിന്റെ സ്ഥിരസ്ഥിതി കൺ‌സ്‌ട്രക്റ്ററുടെ പേരായും ക്ലാസ് ഇൻസ്റ്റാളുചെയ്യുന്നതിലൂടെ സൃഷ്ടിക്കുന്ന ഒബ്‌ജക്റ്റുകളുടെ പേരായും ഉപയോഗിക്കുന്നു; ഈ വ്യതിരിക്തമായ ആശയങ്ങൾ എളുപ്പത്തിൽ പരസ്പരം ബന്ധപ്പെട്ടിരിക്കുന്നു. ആശയക്കുഴപ്പത്തിന്റെ ഘട്ടത്തിൽ, ഒരു ഭാഷയിൽ അതിന്റെ സ്വഭാവ സവിശേഷത കാരണം ഒരു ഭാഷയിൽ അന്തർലീനമായ ഒരു സവിശേഷതയാണെന്നും പോളിമോർഫിസം ഇല്ലാത്ത ഭാഷകളുമായി താരതമ്യപ്പെടുത്തുമ്പോൾ ഈ ഭാഷകൾ എന്തിനാണ് ശക്തവും ചലനാത്മകവും ഉപയോഗത്തിന് അനുയോജ്യവുമാണെന്നും വാദിക്കാൻ കഴിയുന്നത്. അതിനാൽ അവർക്ക് ചലനാത്മക സംവിധാനങ്ങളെ കൂടുതൽ എളുപ്പത്തിൽ മാതൃകയാക്കാൻ കഴിയും.
ഫ്യൂട്ടോൺ ബയസ്: ഫുട്ടൺ ബയസ് എന്നത് ഒരു തരം പ്രസിദ്ധീകരണ പക്ഷപാതമാണ്, അതിലൂടെ പണ്ഡിതന്മാർ അക്കാദമിക് ജേണലുകളെ ഓപ്പൺ ആക്സസ് ഉപയോഗിച്ച് ഉദ്ധരിക്കുന്നു is അതായത് ടോൾ ആക്സസ് പ്രസിദ്ധീകരണങ്ങൾക്ക് മുൻഗണന നൽകിക്കൊണ്ട് അവരുടെ മുഴുവൻ പാഠവും ഇൻറർനെറ്റിൽ ലഭ്യമാക്കുന്ന ജേണലുകൾ. ചില മേഖലകളിലെ പണ്ഡിതന്മാർക്ക് ഓൺ‌ലൈനിൽ ലഭ്യമായ മുഴുവൻ ലേഖനങ്ങളും എളുപ്പത്തിൽ കണ്ടെത്താനും ആക്‌സസ് ചെയ്യാനും കഴിയും, ഇത് രചയിതാക്കൾക്ക് ഈ ലേഖനങ്ങൾ വായിക്കാനും ഉദ്ധരിക്കാനുമുള്ള സാധ്യത വർദ്ധിപ്പിക്കുന്നു, ഇത് ആദ്യം ഉന്നയിച്ചതും പ്രധാനമായും മെഡിക്കൽ ഗവേഷണവുമായി ബന്ധപ്പെട്ട് പഠിച്ചതുമാണ്. തെളിവുകൾ അടിസ്ഥാനമാക്കിയുള്ള മരുന്നിന്റെ പശ്ചാത്തലത്തിൽ, ഓപ്പൺ ആക്സസ് (OA) നൽകാത്ത വിലയേറിയ ജേണലുകളിലെ ലേഖനങ്ങൾ "തെളിവുകൾക്ക് പുറത്തുള്ളവ" ആയിരിക്കാം, ഇത് ഫ്യൂട്ടോൺ പ്രസിദ്ധീകരണങ്ങൾക്ക് കൂടുതൽ ഭാരം നൽകുന്നു. ഓപ്പൺ ആക്‌സസ് ഇല്ലാത്ത ജേണലുകളുമായി താരതമ്യപ്പെടുത്തുമ്പോൾ ഫ്യൂട്ടൺ ബയസ് ഓപ്പൺ ആക്‌സസ് ജേണലുകളുടെ ഇംപാക്ട് ഫാക്ടർ വർദ്ധിപ്പിക്കും.
അമൂർത്ത തന്ത്ര ഗെയിം: കളിയുടെ അനുഭവത്തിന് തീം പ്രധാനമല്ലാത്ത ഒരു തന്ത്ര ഗെയിമാണ് അമൂർത്ത തന്ത്ര ഗെയിം . ലോകത്തെ പല ക്ലാസിക് ബോർഡ് ഗെയിമുകളായ ചെസ്സ്, ഗോ, ചെക്കറുകളും ഡ്രാഫ്റ്റുകളും, സിയാങ്‌കി, ഷോഗി, റിവേർ‌സി, ഒൻപത് പുരുഷന്മാരുടെ മോറിസ്, മിക്ക മങ്കാല വേരിയന്റുകളും ഈ വിഭാഗത്തിൽ‌ ഉൾ‌പ്പെടുന്നു, ഡാമിയോ, ഹൈവ്, യിൻ‌ഷ് എന്നിവപോലുള്ള ആധുനിക ആവർത്തനങ്ങൾ‌ പോലെ .
വിഭാഗം (ഗണിതശാസ്ത്രം): ഗണിതശാസ്ത്രത്തിൽ, "അമ്പടയാളങ്ങളാൽ" ബന്ധിപ്പിച്ചിരിക്കുന്ന "ഒബ്ജക്റ്റുകളുടെ" ഒരു ശേഖരമാണ് ഒരു വിഭാഗം . ഒരു വിഭാഗത്തിന് രണ്ട് അടിസ്ഥാന ഗുണങ്ങളുണ്ട്: അമ്പുകൾ അനുബന്ധമായി രചിക്കാനുള്ള കഴിവ്, ഓരോ ഒബ്ജക്റ്റിനും ഒരു ഐഡന്റിറ്റി അമ്പടയാളം. ഒരു ലളിതമായ ഉദാഹരണം സെറ്റുകളുടെ വിഭാഗമാണ്, ആരുടെ ഒബ്ജക്റ്റുകൾ സെറ്റുകളാണ്, അമ്പടയാളങ്ങൾ ഫംഗ്ഷനുകൾ.
അമൂർത്ത സെൽ സമുച്ചയം: ഗണിതശാസ്ത്രത്തിൽ, അലക്സാണ്ട്രോവ് ടോപ്പോളജി ഉൾക്കൊള്ളുന്ന ഒരു അമൂർത്ത സെറ്റാണ് അമൂർത്ത സെൽ കോംപ്ലക്സ് , അതിൽ ഓരോ പോയിന്റിനും അളവ് എന്ന് വിളിക്കപ്പെടുന്ന നെഗറ്റീവ് അല്ലാത്ത സംഖ്യ സംഖ്യ നിശ്ചയിച്ചിരിക്കുന്നു. യൂക്ലിഡിയൻ, സിഡബ്ല്യു കോംപ്ലക്സുകളിൽ സ്ഥിതി ചെയ്യുന്നതിനാൽ കോശങ്ങളെ "സെല്ലുകൾ" എന്ന് വിളിക്കുന്ന ഹ aus സ്ഡോർഫ് സ്ഥലത്തിന്റെ ഉപവിഭാഗങ്ങളല്ലാത്തതിനാൽ അതിനെ "അമൂർത്ത" എന്ന് വിളിക്കുന്നു. ഇമേജ് വിശകലനത്തിലും കമ്പ്യൂട്ടർ ഗ്രാഫിക്സിലും അമൂർത്ത സെൽ കോംപ്ലക്സുകൾ ഒരു പ്രധാന പങ്ക് വഹിക്കുന്നു.
അമൂർത്ത സെൽ സമുച്ചയം: ഗണിതശാസ്ത്രത്തിൽ, അലക്സാണ്ട്രോവ് ടോപ്പോളജി ഉൾക്കൊള്ളുന്ന ഒരു അമൂർത്ത സെറ്റാണ് അമൂർത്ത സെൽ കോംപ്ലക്സ് , അതിൽ ഓരോ പോയിന്റിനും അളവ് എന്ന് വിളിക്കപ്പെടുന്ന നെഗറ്റീവ് അല്ലാത്ത സംഖ്യ സംഖ്യ നിശ്ചയിച്ചിരിക്കുന്നു. യൂക്ലിഡിയൻ, സിഡബ്ല്യു കോംപ്ലക്സുകളിൽ സ്ഥിതി ചെയ്യുന്നതിനാൽ കോശങ്ങളെ "സെല്ലുകൾ" എന്ന് വിളിക്കുന്ന ഹ aus സ്ഡോർഫ് സ്ഥലത്തിന്റെ ഉപവിഭാഗങ്ങളല്ലാത്തതിനാൽ അതിനെ "അമൂർത്ത" എന്ന് വിളിക്കുന്നു. ഇമേജ് വിശകലനത്തിലും കമ്പ്യൂട്ടർ ഗ്രാഫിക്സിലും അമൂർത്ത സെൽ കോംപ്ലക്സുകൾ ഒരു പ്രധാന പങ്ക് വഹിക്കുന്നു.
സംഗ്രഹ തരം: പ്രോഗ്രാമിംഗ് ഭാഷകളിൽ, നേരിട്ട് തൽക്ഷണം ചെയ്യാൻ കഴിയാത്ത ഒരു നാമനിർദ്ദേശ തരം സിസ്റ്റത്തിലെ ഒരു തരമാണ് അമൂർത്ത തരം ; അമൂർത്തമല്ലാത്ത ഒരു തരം - തൽക്ഷണം ചെയ്യാൻ കഴിയുന്ന - ഒരു കോൺക്രീറ്റ് തരം എന്ന് വിളിക്കുന്നു. ഒരു അമൂർത്ത തരത്തിന്റെ ഓരോ ഉദാഹരണവും ചില കോൺക്രീറ്റ് ഉപതരം ഉദാഹരണമാണ്. അമൂർത്ത തരങ്ങളെ അസ്തിത്വ തരങ്ങൾ എന്നും വിളിക്കുന്നു.
അടയ്ക്കൽ (ഗണിതശാസ്ത്രം): ഗണിതശാസ്ത്രത്തിൽ, സെറ്റിലെ അംഗങ്ങളിൽ ആ പ്രവർത്തനം നടത്തുന്നത് എല്ലായ്പ്പോഴും ആ സെറ്റിലെ ഒരു അംഗത്തെ സൃഷ്ടിക്കുന്നുവെങ്കിൽ ഒരു ഓപ്പറേഷന് കീഴിൽ ഒരു സെറ്റ് അടയ്ക്കും . ഉദാഹരണത്തിന്, പോസിറ്റീവ് പൂർണ്ണസംഖ്യകളാണ് സങ്കലനത്തിനുകീഴിലും, എന്നാൽ കുറയ്ക്കല് കീഴിൽ അടച്ചിടുന്ന: 1 - 2 1 2 രണ്ട് പോസിറ്റീവ് പൂർണ്ണസംഖ്യകളാണ് പോലും ഒരു പോസിറ്റീവ് സംഖ്യ അല്ല. മറ്റൊരു ഉദാഹരണം പൂജ്യം മാത്രമുള്ള സെറ്റ് ആണ്, ഇത് സങ്കലനം, കുറയ്ക്കൽ, ഗുണനം എന്നിവ പ്രകാരം അടച്ചിരിക്കുന്നു.
അടയ്ക്കൽ (ഗണിതശാസ്ത്രം): ഗണിതശാസ്ത്രത്തിൽ, സെറ്റിലെ അംഗങ്ങളിൽ ആ പ്രവർത്തനം നടത്തുന്നത് എല്ലായ്പ്പോഴും ആ സെറ്റിലെ ഒരു അംഗത്തെ സൃഷ്ടിക്കുന്നുവെങ്കിൽ ഒരു ഓപ്പറേഷന് കീഴിൽ ഒരു സെറ്റ് അടയ്ക്കും . ഉദാഹരണത്തിന്, പോസിറ്റീവ് പൂർണ്ണസംഖ്യകളാണ് സങ്കലനത്തിനുകീഴിലും, എന്നാൽ കുറയ്ക്കല് കീഴിൽ അടച്ചിടുന്ന: 1 - 2 1 2 രണ്ട് പോസിറ്റീവ് പൂർണ്ണസംഖ്യകളാണ് പോലും ഒരു പോസിറ്റീവ് സംഖ്യ അല്ല. മറ്റൊരു ഉദാഹരണം പൂജ്യം മാത്രമുള്ള സെറ്റ് ആണ്, ഇത് സങ്കലനം, കുറയ്ക്കൽ, ഗുണനം എന്നിവ പ്രകാരം അടച്ചിരിക്കുന്നു.
അമൂർത്ത കോമിക്സ്: വിഷ്വൽ അമൂർത്തതയെക്കുറിച്ചുള്ള ആശയങ്ങൾ കോമിക് സ്ട്രിപ്പിന്റെ പരമ്പരാഗത തുടർച്ചയുമായി സംയോജിപ്പിക്കുന്ന കോമിക്സുകളാണ് അമൂർത്ത കോമിക്സ് .
അമൂർത്ത യന്ത്രം: ഒരു അമൂർത്ത കമ്പ്യൂട്ടർ എന്നും വിളിക്കപ്പെടുന്ന ഒരു അമൂർത്ത യന്ത്രം ഒരു കമ്പ്യൂട്ടർ മാതൃക നിർവചിക്കാൻ ഉപയോഗിക്കുന്ന ഒരു സൈദ്ധാന്തിക കമ്പ്യൂട്ടറാണ്. കമ്പ്യൂട്ടർ സയൻസ്, കമ്പ്യൂട്ടർ എഞ്ചിനീയറിംഗ് വിഭാഗങ്ങളിൽ കമ്പ്യൂട്ടിംഗ് പ്രക്രിയകളുടെ സംഗ്രഹം ഉപയോഗിക്കുന്നു, മാത്രമല്ല ഇത് ഒരു പ്രത്യേക സമയ മാതൃകയെ കണക്കാക്കുന്നു.
ആശയം: ആശയങ്ങൾ, അബ്സ്ട്രാക്റ്റ് ആശയങ്ങളോ മനസ്സിൽ സംഭവിക്കുന്ന പൊതു സങ്കൽപങ്ങളിൽ നിർവചിച്ചിരിക്കുന്നത് പ്രസംഗത്തിൽ, ആശയമോ ൽ ചെയ്യുന്നു. ചിന്തകളുടെയും വിശ്വാസങ്ങളുടെയും അടിസ്ഥാന നിർമാണഘടകങ്ങളാണിവ. വിജ്ഞാനത്തിന്റെ എല്ലാ വശങ്ങളിലും അവ ഒരു പ്രധാന പങ്ക് വഹിക്കുന്നു. അതുപോലെ, ഭാഷാശാസ്ത്രം, മന psych ശാസ്ത്രം, തത്ത്വചിന്ത എന്നിങ്ങനെയുള്ള നിരവധി വിഷയങ്ങൾ ആശയങ്ങൾ പഠിക്കുന്നു, കൂടാതെ ഈ വിഷയങ്ങൾ ആശയങ്ങളുടെ യുക്തിപരവും മന psych ശാസ്ത്രപരവുമായ ഘടനയെക്കുറിച്ചും ചിന്തകളും വാക്യങ്ങളും എങ്ങനെ രൂപപ്പെടുത്തുന്നുവെന്നും താൽപ്പര്യപ്പെടുന്നു. കോഗ്നിറ്റീവ് സയൻസ് എന്നറിയപ്പെടുന്ന വളർന്നുവരുന്ന ഇന്റർ ഡിസിപ്ലിനറി സമീപനത്തിന്റെ ഒരു പ്രധാന ഘടകമാണ് ആശയങ്ങളെക്കുറിച്ചുള്ള പഠനം.
സംഗ്രഹം: നിർദ്ദിഷ്ട ഉദാഹരണങ്ങൾ, അക്ഷര സൂചകങ്ങൾ, ആദ്യ തത്ത്വങ്ങൾ അല്ലെങ്കിൽ മറ്റ് രീതികളുടെ ഉപയോഗത്തിൽ നിന്നും വർഗ്ഗീകരണത്തിൽ നിന്നും പൊതുവായ നിയമങ്ങളും ആശയങ്ങളും ഉരുത്തിരിഞ്ഞ ഒരു ആശയപരമായ പ്രക്രിയയാണ് അതിന്റെ പ്രധാന അർത്ഥത്തിൽ അമൂർത്തീകരണം .
അമൂർത്ത ഡാറ്റ തരം: കമ്പ്യൂട്ടർ സയൻസിൽ, ഡാറ്റ തരങ്ങൾക്കുള്ള ഗണിതശാസ്ത്ര മോഡലാണ് അമൂർത്ത ഡാറ്റാ തരം ( ADT ). ഒരു ഉപയോക്താവിന്റെ കാഴ്ചപ്പാടിൽ നിന്ന്, ഡാറ്റയുടെ, പ്രത്യേകിച്ചും സാധ്യമായ മൂല്യങ്ങൾ, ഈ തരത്തിലുള്ള ഡാറ്റയിൽ സാധ്യമായ പ്രവർത്തനങ്ങൾ, ഈ പ്രവർത്തനങ്ങളുടെ പെരുമാറ്റം എന്നിവയിൽ നിന്ന് ഒരു അമൂർത്ത ഡാറ്റാ തരം അതിന്റെ പെരുമാറ്റം (സെമാന്റിക്സ്) നിർവചിക്കുന്നു. ഈ ഗണിതശാസ്ത്ര മാതൃക ഡാറ്റാ ഘടനകളുമായി വിരുദ്ധമാണ്, അവ ഡാറ്റയുടെ ദൃ represent മായ പ്രാതിനിധ്യങ്ങളാണ്, മാത്രമല്ല ഇത് ഒരു ഉപയോക്താവല്ല, നടപ്പിലാക്കുന്നവന്റെ കാഴ്ചപ്പാടാണ്.
അമൂർത്ത ഡാറ്റ തരം: കമ്പ്യൂട്ടർ സയൻസിൽ, ഡാറ്റ തരങ്ങൾക്കുള്ള ഗണിതശാസ്ത്ര മോഡലാണ് അമൂർത്ത ഡാറ്റാ തരം ( ADT ). ഒരു ഉപയോക്താവിന്റെ കാഴ്ചപ്പാടിൽ നിന്ന്, ഡാറ്റയുടെ, പ്രത്യേകിച്ചും സാധ്യമായ മൂല്യങ്ങൾ, ഈ തരത്തിലുള്ള ഡാറ്റയിൽ സാധ്യമായ പ്രവർത്തനങ്ങൾ, ഈ പ്രവർത്തനങ്ങളുടെ പെരുമാറ്റം എന്നിവയിൽ നിന്ന് ഒരു അമൂർത്ത ഡാറ്റാ തരം അതിന്റെ പെരുമാറ്റം (സെമാന്റിക്സ്) നിർവചിക്കുന്നു. ഈ ഗണിതശാസ്ത്ര മാതൃക ഡാറ്റാ ഘടനകളുമായി വിരുദ്ധമാണ്, അവ ഡാറ്റയുടെ ദൃ represent മായ പ്രാതിനിധ്യങ്ങളാണ്, മാത്രമല്ല ഇത് ഒരു ഉപയോക്താവല്ല, നടപ്പിലാക്കുന്നവന്റെ കാഴ്ചപ്പാടാണ്.
അമൂർത്ത ഡാറ്റ തരം: കമ്പ്യൂട്ടർ സയൻസിൽ, ഡാറ്റ തരങ്ങൾക്കുള്ള ഗണിതശാസ്ത്ര മോഡലാണ് അമൂർത്ത ഡാറ്റാ തരം ( ADT ). ഒരു ഉപയോക്താവിന്റെ കാഴ്ചപ്പാടിൽ നിന്ന്, ഡാറ്റയുടെ, പ്രത്യേകിച്ചും സാധ്യമായ മൂല്യങ്ങൾ, ഈ തരത്തിലുള്ള ഡാറ്റയിൽ സാധ്യമായ പ്രവർത്തനങ്ങൾ, ഈ പ്രവർത്തനങ്ങളുടെ പെരുമാറ്റം എന്നിവയിൽ നിന്ന് ഒരു അമൂർത്ത ഡാറ്റാ തരം അതിന്റെ പെരുമാറ്റം (സെമാന്റിക്സ്) നിർവചിക്കുന്നു. ഈ ഗണിതശാസ്ത്ര മാതൃക ഡാറ്റാ ഘടനകളുമായി വിരുദ്ധമാണ്, അവ ഡാറ്റയുടെ ദൃ represent മായ പ്രാതിനിധ്യങ്ങളാണ്, മാത്രമല്ല ഇത് ഒരു ഉപയോക്താവല്ല, നടപ്പിലാക്കുന്നവന്റെ കാഴ്ചപ്പാടാണ്.
അമൂർത്ത ഡാറ്റ തരം: കമ്പ്യൂട്ടർ സയൻസിൽ, ഡാറ്റ തരങ്ങൾക്കുള്ള ഗണിതശാസ്ത്ര മോഡലാണ് അമൂർത്ത ഡാറ്റാ തരം ( ADT ). ഒരു ഉപയോക്താവിന്റെ കാഴ്ചപ്പാടിൽ നിന്ന്, ഡാറ്റയുടെ, പ്രത്യേകിച്ചും സാധ്യമായ മൂല്യങ്ങൾ, ഈ തരത്തിലുള്ള ഡാറ്റയിൽ സാധ്യമായ പ്രവർത്തനങ്ങൾ, ഈ പ്രവർത്തനങ്ങളുടെ പെരുമാറ്റം എന്നിവയിൽ നിന്ന് ഒരു അമൂർത്ത ഡാറ്റാ തരം അതിന്റെ പെരുമാറ്റം (സെമാന്റിക്സ്) നിർവചിക്കുന്നു. ഈ ഗണിതശാസ്ത്ര മാതൃക ഡാറ്റാ ഘടനകളുമായി വിരുദ്ധമാണ്, അവ ഡാറ്റയുടെ ദൃ represent മായ പ്രാതിനിധ്യങ്ങളാണ്, മാത്രമല്ല ഇത് ഒരു ഉപയോക്താവല്ല, നടപ്പിലാക്കുന്നവന്റെ കാഴ്ചപ്പാടാണ്.
അമൂർത്ത ഡാറ്റ തരം: കമ്പ്യൂട്ടർ സയൻസിൽ, ഡാറ്റ തരങ്ങൾക്കുള്ള ഗണിതശാസ്ത്ര മോഡലാണ് അമൂർത്ത ഡാറ്റാ തരം ( ADT ). ഒരു ഉപയോക്താവിന്റെ കാഴ്ചപ്പാടിൽ നിന്ന്, ഡാറ്റയുടെ, പ്രത്യേകിച്ചും സാധ്യമായ മൂല്യങ്ങൾ, ഈ തരത്തിലുള്ള ഡാറ്റയിൽ സാധ്യമായ പ്രവർത്തനങ്ങൾ, ഈ പ്രവർത്തനങ്ങളുടെ പെരുമാറ്റം എന്നിവയിൽ നിന്ന് ഒരു അമൂർത്ത ഡാറ്റാ തരം അതിന്റെ പെരുമാറ്റം (സെമാന്റിക്സ്) നിർവചിക്കുന്നു. ഈ ഗണിതശാസ്ത്ര മാതൃക ഡാറ്റാ ഘടനകളുമായി വിരുദ്ധമാണ്, അവ ഡാറ്റയുടെ ദൃ represent മായ പ്രാതിനിധ്യങ്ങളാണ്, മാത്രമല്ല ഇത് ഒരു ഉപയോക്താവല്ല, നടപ്പിലാക്കുന്നവന്റെ കാഴ്ചപ്പാടാണ്.
അമൂർത്ത കല: ലോകത്തിലെ വിഷ്വൽ റഫറൻസുകളിൽ നിന്ന് ഒരു പരിധിവരെ സ്വാതന്ത്ര്യത്തോടുകൂടിയ ഒരു രചന സൃഷ്ടിക്കാൻ അമൂർത്ത കല രൂപം, രൂപം, നിറം, രേഖ എന്നിവയുടെ വിഷ്വൽ ഭാഷ ഉപയോഗിക്കുന്നു. പാശ്ചാത്യ കല, നവോത്ഥാനം മുതൽ പത്തൊൻപതാം നൂറ്റാണ്ടിന്റെ മദ്ധ്യകാലം വരെ, കാഴ്ചപ്പാടിന്റെ യുക്തിയും ദൃശ്യമായ യാഥാർത്ഥ്യത്തിന്റെ ഒരു മിഥ്യാധാരണയെ പുനർനിർമ്മിക്കാനുള്ള ശ്രമവുമാണ്. പത്തൊൻപതാം നൂറ്റാണ്ടിന്റെ അവസാനത്തോടെ സാങ്കേതികവിദ്യ, ശാസ്ത്രം, തത്ത്വചിന്ത എന്നിവയിൽ സംഭവിക്കുന്ന അടിസ്ഥാനപരമായ മാറ്റങ്ങൾ ഉൾക്കൊള്ളുന്ന ഒരു പുതിയ തരം കല സൃഷ്ടിക്കേണ്ടതുണ്ടെന്ന് പല കലാകാരന്മാർക്കും തോന്നി. വ്യക്തിഗത കലാകാരന്മാർ അവരുടെ സൈദ്ധാന്തിക വാദങ്ങൾ ഉന്നയിച്ച ഉറവിടങ്ങൾ വൈവിധ്യപൂർണ്ണമായിരുന്നു, അക്കാലത്ത് പാശ്ചാത്യ സംസ്കാരത്തിന്റെ എല്ലാ മേഖലകളിലെയും സാമൂഹികവും ബ ual ദ്ധികവുമായ മുൻ‌തൂക്കങ്ങൾ പ്രതിഫലിപ്പിച്ചു.
അമൂർത്തവും കോൺക്രീറ്റും: മെറ്റാഫിസിക്‌സിൽ, അമൂർത്തവും കോൺക്രീറ്റും തമ്മിലുള്ള വ്യത്യാസം രണ്ട് തരം എന്റിറ്റികൾ തമ്മിലുള്ള വിഭജനത്തെ സൂചിപ്പിക്കുന്നു. ഈ വ്യത്യാസത്തിന് അടിസ്ഥാന മെറ്റാഫിസിക്കൽ പ്രാധാന്യമുണ്ടെന്ന് പല തത്ത്വചിന്തകരും അഭിപ്രായപ്പെടുന്നു. കോൺക്രീറ്റ് വസ്തുക്കളുടെ ഉദാഹരണങ്ങളിൽ സസ്യങ്ങൾ, മനുഷ്യർ, ഗ്രഹങ്ങൾ എന്നിവ ഉൾപ്പെടുന്നു, അതേസമയം സംഖ്യകൾ, സെറ്റുകൾ, നിർദ്ദേശങ്ങൾ എന്നിവ അമൂർത്ത വസ്തുക്കളാണ് . ദൃ ret തയുടെയും അമൂർത്തതയുടെയും സ്വഭാവ ചിഹ്നങ്ങൾ എന്താണെന്നതിന് പൊതുവായ അഭിപ്രായ സമന്വയമില്ല. (1) സ്ഥല-സമയത്തിനകത്തോ പുറത്തോ ഉള്ള അസ്തിത്വം, (2) കാരണങ്ങളും ഫലങ്ങളും ഉണ്ടോ ഇല്ലയോ, (3) അനിശ്ചിതത്വത്തിലോ ആവശ്യമുള്ളതോ ഉള്ള അസ്തിത്വം, (4) പ്രത്യേകമോ സാർവത്രികമോ (5) ശാരീരികമോ മാനസികമോ ആയ മേഖലയിലോ അല്ലാതെയോ. ഈ വൈവിധ്യമാർന്ന കാഴ്ചപ്പാടുകൾ ഉണ്ടായിരുന്നിട്ടും, മിക്ക വസ്തുക്കളും അമൂർത്തമോ കോൺക്രീറ്റോ ആണോ എന്നതിനെക്കുറിച്ച് വിശാലമായ ധാരണയുണ്ട്. അതിനാൽ മിക്ക വ്യാഖ്യാനങ്ങളിലും, ഈ കാഴ്ചപ്പാടുകളെല്ലാം സമ്മതിക്കും, ഉദാഹരണത്തിന്, സസ്യങ്ങൾ കോൺക്രീറ്റ് വസ്തുക്കളാണ്, അക്കങ്ങൾ അമൂർത്ത വസ്തുക്കളാണ്.
അമൂർത്ത ഡിഫറൻഷ്യൽ സമവാക്യം: ഗണിതശാസ്ത്രത്തിൽ, ഒരു അബ്സ്ട്രാക്ട് ഡിഫറൻഷ്യൽ സമവാക്യം ഒരു ഡിഫറൻഷ്യൽ സമവാക്യമാണ്, അതിൽ അജ്ഞാതമായ പ്രവർത്തനവും അതിന്റെ ഡെറിവേറ്റീവുകളും ചില ജനറിക് അമൂർത്ത സ്ഥലത്ത് മൂല്യങ്ങൾ എടുക്കുന്നു. ഭാഗിക ഡിഫറൻഷ്യൽ സമവാക്യങ്ങളുടെ പഠനത്തിൽ ഇത്തരത്തിലുള്ള സമവാക്യങ്ങൾ ഉയർന്നുവരുന്നു: വേരിയബിളുകളിലൊന്നിന് ഒരു പ്രത്യേക പദവി നൽകുകയും മറ്റുള്ളവയെല്ലാം ഒരുമിച്ച് ചേർക്കുകയും ചെയ്താൽ, തെളിവുകളിൽ ഉൾപ്പെടുത്തിയിട്ടുള്ള വേരിയബിളിനെ സംബന്ധിച്ച് ഒരു സാധാരണ "ഡിഫറൻഷ്യൽ" സമവാക്യം ലഭിച്ചു. ചില സ function കര്യപ്രദമായ ഫംഗ്ഷൻ സ്പെയ്സുകളിൽ പരിഹാരങ്ങൾ പരിഗണിച്ച് അതിർത്തി വ്യവസ്ഥകൾ ചേർക്കുന്നത് പലപ്പോഴും വിവർത്തനം ചെയ്യാനാകും.
അമൂർത്ത ഡിഫറൻഷ്യൽ ജ്യാമിതി: അബ്‌സ്ട്രാക്റ്റ് എന്ന നാമവിശേഷണം മുമ്പ് ഡിഫറൻഷ്യൽ ജ്യാമിതിയിൽ പലപ്പോഴും പ്രയോഗിക്കപ്പെട്ടിട്ടുണ്ട്, എന്നാൽ ഈ ലേഖനത്തിന്റെ അമൂർത്ത ഡിഫറൻഷ്യൽ ജ്യാമിതി (എ.ഡി.ജി) സുഗമതയെക്കുറിച്ചുള്ള കാൽക്കുലസ് സങ്കൽപ്പമില്ലാതെ ഡിഫറൻഷ്യൽ ജ്യാമിതിയുടെ ഒരു രൂപമാണ്, 1998 മുതൽ അനസ്താസിയോസ് മല്ലിയോസും ഇയോന്നിസ് റാപ്റ്റിസും വികസിപ്പിച്ചെടുത്തത്.
ചലനാത്മക സിസ്റ്റങ്ങളുടെയും ഡിഫറൻഷ്യൽ സമവാക്യ വിഷയങ്ങളുടെയും പട്ടിക: വിക്കിപീഡിയ പേജ് ചലനാത്മക സംവിധാനത്തിന്റെയും ഡിഫറൻഷ്യൽ സമവാക്യ വിഷയങ്ങളുടെയും പട്ടികയാണിത് . ഭാഗിക ഡിഫറൻഷ്യൽ സമവാക്യ വിഷയങ്ങളുടെ പട്ടിക, സമവാക്യങ്ങളുടെ പട്ടിക എന്നിവയും കാണുക.
അമൂർത്ത സമ്പദ്‌വ്യവസ്ഥ: സൈദ്ധാന്തിക സാമ്പത്തിക ശാസ്ത്രത്തിൽ, മൈക്രോ ഇക്കണോമിക്സിലെ ഒരു എക്സ്ചേഞ്ച് സമ്പദ്‌വ്യവസ്ഥയുടെ സ്റ്റാൻഡേർഡ് മോഡലിനെയും ഗെയിം തിയറിയിലെ ഗെയിമിന്റെ സ്റ്റാൻഡേർഡ് മോഡലിനെയും സാമാന്യവൽക്കരിക്കുന്ന ഒരു മാതൃകയാണ് അമൂർത്ത സമ്പദ്‌വ്യവസ്ഥ . അമൂർത്തമായ സമ്പദ് ഭൂമോപരിതലത്തിലെ മൈക്രോഇക്കണോമിക്സ് ഒരു വല്രസിഅന് സന്തുലനത്തിന്റെ ഇരുവരും ഇടാം, ഗെയിം-സിദ്ധാന്തം ഒരു നാഷ് സന്തുലനത്തിന്റെ.
അമൂർത്ത പ്രാഥമിക ക്ലാസ്: മോഡൽ സിദ്ധാന്തത്തിൽ, ഗണിതശാസ്ത്ര യുക്തിക്കുള്ളിലെ ഒരു അച്ചടക്കം, ഒരു അമൂർത്ത പ്രാഥമിക ക്ലാസ് അല്ലെങ്കിൽ ചുരുക്കത്തിൽ AEC , ഫസ്റ്റ് ഓർഡർ മോഡൽ സിദ്ധാന്തത്തിലെ ഒരു പ്രാഥമിക ക്ലാസിന്റെ പ്രാഥമിക സബ്‌സ്ട്രക്ചറുമായി ബന്ധിപ്പിക്കുന്നതിന് സമാനമായ ഭാഗിക ക്രമമുള്ള മോഡലുകളുടെ ഒരു വിഭാഗമാണ്. സഹാറൻ ഷെലയാണ് അവ അവതരിപ്പിച്ചത്.
ഉൾച്ചേർക്കൽ: ഗണിതശാസ്ത്രത്തിൽ, ഒരു ഉപഗ്രൂപ്പായ ഒരു ഗ്രൂപ്പ് പോലുള്ള മറ്റൊരു ഗണിതഘടനയുടെ മറ്റൊരു ഉദാഹരണമാണ് ഉൾച്ചേർക്കൽ .
സോഷ്യോളജിക്കൽ ഇമാജിനേഷൻ: അമേരിക്കൻ സോഷ്യോളജിസ്റ്റ് സി. റൈറ്റ് മിൽസ് 1959 ൽ ഓക്സ്ഫോർഡ് യൂണിവേഴ്സിറ്റി പ്രസ്സ് പ്രസിദ്ധീകരിച്ച പുസ്തകമാണ് ദി സോഷ്യോളജിക്കൽ ഇമാജിനേഷൻ . അതിൽ, സാമൂഹ്യശാസ്ത്ര ഭാവന എന്ന ആശയം അദ്ദേഹം വികസിപ്പിച്ചെടുക്കുന്നു, സ്വയവും സമൂഹവും തമ്മിലുള്ള ബന്ധം മനസ്സിലാക്കാൻ കഴിയുന്ന മാർഗ്ഗം.
അമൂർത്തവും കോൺക്രീറ്റും: മെറ്റാഫിസിക്‌സിൽ, അമൂർത്തവും കോൺക്രീറ്റും തമ്മിലുള്ള വ്യത്യാസം രണ്ട് തരം എന്റിറ്റികൾ തമ്മിലുള്ള വിഭജനത്തെ സൂചിപ്പിക്കുന്നു. ഈ വ്യത്യാസത്തിന് അടിസ്ഥാന മെറ്റാഫിസിക്കൽ പ്രാധാന്യമുണ്ടെന്ന് പല തത്ത്വചിന്തകരും അഭിപ്രായപ്പെടുന്നു. കോൺക്രീറ്റ് വസ്തുക്കളുടെ ഉദാഹരണങ്ങളിൽ സസ്യങ്ങൾ, മനുഷ്യർ, ഗ്രഹങ്ങൾ എന്നിവ ഉൾപ്പെടുന്നു, അതേസമയം സംഖ്യകൾ, സെറ്റുകൾ, നിർദ്ദേശങ്ങൾ എന്നിവ അമൂർത്ത വസ്തുക്കളാണ് . ദൃ ret തയുടെയും അമൂർത്തതയുടെയും സ്വഭാവ ചിഹ്നങ്ങൾ എന്താണെന്നതിന് പൊതുവായ അഭിപ്രായ സമന്വയമില്ല. (1) സ്ഥല-സമയത്തിനകത്തോ പുറത്തോ ഉള്ള അസ്തിത്വം, (2) കാരണങ്ങളും ഫലങ്ങളും ഉണ്ടോ ഇല്ലയോ, (3) അനിശ്ചിതത്വത്തിലോ ആവശ്യമുള്ളതോ ഉള്ള അസ്തിത്വം, (4) പ്രത്യേകമോ സാർവത്രികമോ (5) ശാരീരികമോ മാനസികമോ ആയ മേഖലയിലോ അല്ലാതെയോ. ഈ വൈവിധ്യമാർന്ന കാഴ്ചപ്പാടുകൾ ഉണ്ടായിരുന്നിട്ടും, മിക്ക വസ്തുക്കളും അമൂർത്തമോ കോൺക്രീറ്റോ ആണോ എന്നതിനെക്കുറിച്ച് വിശാലമായ ധാരണയുണ്ട്. അതിനാൽ മിക്ക വ്യാഖ്യാനങ്ങളിലും, ഈ കാഴ്ചപ്പാടുകളെല്ലാം സമ്മതിക്കും, ഉദാഹരണത്തിന്, സസ്യങ്ങൾ കോൺക്രീറ്റ് വസ്തുക്കളാണ്, അക്കങ്ങൾ അമൂർത്ത വസ്തുക്കളാണ്.
അസ്തിത്വവാദം: അസ്തിത്വവാദം (അല്ലെങ്കിൽ) എന്നത് മനുഷ്യന്റെ നിലനിൽപ്പിന്റെ പ്രശ്നം പര്യവേക്ഷണം ചെയ്യുന്ന ഒരു വ്യക്തിയുടെ ചിന്തയുടെയും വികാരത്തിന്റെയും അഭിനയത്തിന്റെയും ജീവിതാനുഭവത്തെ കേന്ദ്രീകരിക്കുന്ന ഒരു ദാർശനിക അന്വേഷണമാണ്. അസ്തിത്വവാദിയുടെ വീക്ഷണത്തിൽ, വ്യക്തിയുടെ ആരംഭ പോയിന്റിനെ "അസ്തിത്വപരമായ ഭയം" എന്ന് വിളിക്കുന്നു, പ്രത്യക്ഷത്തിൽ അർത്ഥശൂന്യമായ അല്ലെങ്കിൽ അസംബന്ധമായ ഒരു ലോകത്തിന് മുന്നിൽ ഭയം, വഴിതെറ്റിക്കൽ, ആശയക്കുഴപ്പം അല്ലെങ്കിൽ ഉത്കണ്ഠ. അസ്തിത്വവാദ ചിന്തകർ മനുഷ്യ അസ്തിത്വത്തിന്റെ അർത്ഥം, ലക്ഷ്യം, മൂല്യം എന്നിവയുമായി ബന്ധപ്പെട്ട പ്രശ്നങ്ങൾ പതിവായി പര്യവേക്ഷണം ചെയ്യുന്നു.
അമൂർത്ത പദപ്രയോഗം: 1940 കളിൽ ന്യൂയോർക്കിൽ വികസിപ്പിച്ച അമേരിക്കൻ പെയിന്റിംഗിലെ രണ്ടാം ലോക മഹായുദ്ധാനന്തര കലാ പ്രസ്ഥാനമാണ് അമൂർത്ത എക്സ്പ്രഷനിസം . അന്താരാഷ്ട്ര സ്വാധീനം നേടുകയും ന്യൂയോർക്ക് നഗരത്തെ പാശ്ചാത്യ കലാ ലോകത്തിന്റെ കേന്ദ്രത്തിൽ ഉൾപ്പെടുത്തുകയും ചെയ്ത ആദ്യത്തെ അമേരിക്കൻ പ്രസ്ഥാനമാണിത്. മുമ്പ് പാരീസ് നിറച്ച ഈ പങ്ക്. "അമൂർത്ത എക്സ്പ്രഷനിസം" എന്ന പദം അമേരിക്കൻ കലയിൽ ആദ്യമായി കലാ നിരൂപകനായ റോബർട്ട് കോട്ട്സ് പ്രയോഗിച്ചെങ്കിലും, ജർമ്മൻ എക്സ്പ്രഷനിസത്തെക്കുറിച്ച് 1919 ൽ ജർമ്മനിയിൽ ആദ്യമായി ഡെർ സ്റ്റർം മാസികയിൽ ഇത് ഉപയോഗിച്ചു. അമേരിക്കൻ ഐക്യനാടുകളിൽ, വാസിലി കാൻഡിൻസ്കിയുടെ കൃതികളുമായി ബന്ധപ്പെട്ട് 1929 ൽ ആദ്യമായി ഈ പദം ഉപയോഗിച്ചതാണ് ആൽഫ്രഡ് ബാർ.
അമൂർത്ത പദപ്രയോഗം: 1940 കളിൽ ന്യൂയോർക്കിൽ വികസിപ്പിച്ച അമേരിക്കൻ പെയിന്റിംഗിലെ രണ്ടാം ലോക മഹായുദ്ധാനന്തര കലാ പ്രസ്ഥാനമാണ് അമൂർത്ത എക്സ്പ്രഷനിസം . അന്താരാഷ്ട്ര സ്വാധീനം നേടുകയും ന്യൂയോർക്ക് നഗരത്തെ പാശ്ചാത്യ കലാ ലോകത്തിന്റെ കേന്ദ്രത്തിൽ ഉൾപ്പെടുത്തുകയും ചെയ്ത ആദ്യത്തെ അമേരിക്കൻ പ്രസ്ഥാനമാണിത്. മുമ്പ് പാരീസ് നിറച്ച ഈ പങ്ക്. "അമൂർത്ത എക്സ്പ്രഷനിസം" എന്ന പദം അമേരിക്കൻ കലയിൽ ആദ്യമായി കലാ നിരൂപകനായ റോബർട്ട് കോട്ട്സ് പ്രയോഗിച്ചെങ്കിലും, ജർമ്മൻ എക്സ്പ്രഷനിസത്തെക്കുറിച്ച് 1919 ൽ ജർമ്മനിയിൽ ആദ്യമായി ഡെർ സ്റ്റർം മാസികയിൽ ഇത് ഉപയോഗിച്ചു. അമേരിക്കൻ ഐക്യനാടുകളിൽ, വാസിലി കാൻഡിൻസ്കിയുടെ കൃതികളുമായി ബന്ധപ്പെട്ട് 1929 ൽ ആദ്യമായി ഈ പദം ഉപയോഗിച്ചതാണ് ആൽഫ്രഡ് ബാർ.