Abstract expressionism, Abstract expressionism, Abstract factory pattern

അമൂർത്ത പദപ്രയോഗം: 1940 കളിൽ ന്യൂയോർക്കിൽ വികസിപ്പിച്ച അമേരിക്കൻ പെയിന്റിംഗിലെ രണ്ടാം ലോക മഹായുദ്ധാനന്തര കലാ പ്രസ്ഥാനമാണ് അമൂർത്ത എക്സ്പ്രഷനിസം . അന്താരാഷ്ട്ര സ്വാധീനം നേടുകയും ന്യൂയോർക്ക് നഗരത്തെ പാശ്ചാത്യ കലാ ലോകത്തിന്റെ കേന്ദ്രത്തിൽ ഉൾപ്പെടുത്തുകയും ചെയ്ത ആദ്യത്തെ അമേരിക്കൻ പ്രസ്ഥാനമായിരുന്നു ഇത്, മുമ്പ് പാരീസ് നിറച്ച ഈ പങ്ക്. "അമൂർത്ത എക്സ്പ്രഷനിസം" എന്ന പദം അമേരിക്കൻ കലയിൽ ആദ്യമായി കലാവിമർശകൻ റോബർട്ട് കോട്ട്സ് പ്രയോഗിച്ചെങ്കിലും, ജർമ്മനിയിൽ ആദ്യമായി 1919 ൽ ജർമ്മനിയിൽ ഡെർ സ്റ്റർം മാസികയിൽ ജർമ്മൻ എക്സ്പ്രഷനിസത്തെക്കുറിച്ച് ഉപയോഗിച്ചു. അമേരിക്കൻ ഐക്യനാടുകളിൽ, വാസിലി കാൻഡിൻസ്കിയുടെ കൃതികളുമായി ബന്ധപ്പെട്ട് 1929 ൽ ആദ്യമായി ഈ പദം ഉപയോഗിച്ചതാണ് ആൽഫ്രഡ് ബാർ.
അമൂർത്ത പദപ്രയോഗം: 1940 കളിൽ ന്യൂയോർക്കിൽ വികസിപ്പിച്ച അമേരിക്കൻ പെയിന്റിംഗിലെ രണ്ടാം ലോക മഹായുദ്ധാനന്തര കലാ പ്രസ്ഥാനമാണ് അമൂർത്ത എക്സ്പ്രഷനിസം . അന്താരാഷ്ട്ര സ്വാധീനം നേടുകയും ന്യൂയോർക്ക് നഗരത്തെ പാശ്ചാത്യ കലാ ലോകത്തിന്റെ കേന്ദ്രത്തിൽ ഉൾപ്പെടുത്തുകയും ചെയ്ത ആദ്യത്തെ അമേരിക്കൻ പ്രസ്ഥാനമായിരുന്നു ഇത്, മുമ്പ് പാരീസ് നിറച്ച ഈ പങ്ക്. "അമൂർത്ത എക്സ്പ്രഷനിസം" എന്ന പദം അമേരിക്കൻ കലയിൽ ആദ്യമായി കലാവിമർശകൻ റോബർട്ട് കോട്ട്സ് പ്രയോഗിച്ചെങ്കിലും, ജർമ്മനിയിൽ ആദ്യമായി 1919 ൽ ജർമ്മനിയിൽ ഡെർ സ്റ്റർം മാസികയിൽ ജർമ്മൻ എക്സ്പ്രഷനിസത്തെക്കുറിച്ച് ഉപയോഗിച്ചു. അമേരിക്കൻ ഐക്യനാടുകളിൽ, വാസിലി കാൻഡിൻസ്കിയുടെ കൃതികളുമായി ബന്ധപ്പെട്ട് 1929 ൽ ആദ്യമായി ഈ പദം ഉപയോഗിച്ചതാണ് ആൽഫ്രഡ് ബാർ.
അമൂർത്ത ഫാക്ടറി പാറ്റേൺ: അമൂർത്തമായ ഫാക്ടറി പാറ്റേൺ ഒരു കൂട്ടം വ്യക്തിഗത ഫാക്ടറികളുടെ കോൺക്രീറ്റ് ക്ലാസുകൾ വ്യക്തമാക്കാതെ ഒരു പൊതു തീം ഉൾക്കൊള്ളുന്ന ഒരു മാർഗ്ഗം ഉൾക്കൊള്ളുന്നു. സാധാരണ ഉപയോഗത്തിൽ, ക്ലയന്റ് സോഫ്റ്റ്വെയർ അമൂർത്ത ഫാക്ടറിയുടെ ഒരു ശക്തമായ നടപ്പാക്കൽ സൃഷ്ടിക്കുകയും തുടർന്ന് തീമിന്റെ ഭാഗമായ കോൺക്രീറ്റ് വസ്തുക്കൾ സൃഷ്ടിക്കുന്നതിന് ഫാക്ടറിയുടെ ജനറിക് ഇന്റർഫേസ് ഉപയോഗിക്കുകയും ചെയ്യുന്നു. ഈ ആന്തരിക ഫാക്ടറികളിൽ നിന്ന് ഏത് കോൺക്രീറ്റ് വസ്തുക്കൾ ലഭിക്കുന്നുവെന്ന് ക്ലയന്റിന് അറിയില്ല, കാരണം ഇത് അവരുടെ ഉൽപ്പന്നങ്ങളുടെ ജനറിക് ഇന്റർഫേസുകൾ മാത്രം ഉപയോഗിക്കുന്നു. ഫാക്ടറി ഇന്റർഫേസിൽ തുറന്നുകാണിക്കുന്ന രീതികളിൽ ഒബ്ജക്റ്റ് സൃഷ്ടിക്കൽ നടപ്പിലാക്കുന്നതിനാൽ ഈ പാറ്റേൺ ഒരു കൂട്ടം ഒബ്ജക്റ്റുകൾ അവയുടെ പൊതുവായ ഉപയോഗത്തിൽ നിന്ന് വേർതിരിക്കുകയും ഒബ്ജക്റ്റ് കോമ്പോസിഷനെ ആശ്രയിക്കുകയും ചെയ്യുന്നു.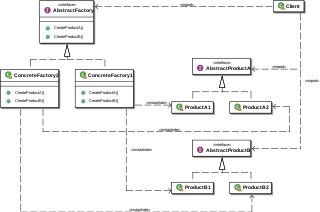
അമൂർത്ത ഫാക്ടറി പാറ്റേൺ: അമൂർത്തമായ ഫാക്ടറി പാറ്റേൺ ഒരു കൂട്ടം വ്യക്തിഗത ഫാക്ടറികളുടെ കോൺക്രീറ്റ് ക്ലാസുകൾ വ്യക്തമാക്കാതെ ഒരു പൊതു തീം ഉൾക്കൊള്ളുന്ന ഒരു മാർഗ്ഗം ഉൾക്കൊള്ളുന്നു. സാധാരണ ഉപയോഗത്തിൽ, ക്ലയന്റ് സോഫ്റ്റ്വെയർ അമൂർത്ത ഫാക്ടറിയുടെ ഒരു ശക്തമായ നടപ്പാക്കൽ സൃഷ്ടിക്കുകയും തുടർന്ന് തീമിന്റെ ഭാഗമായ കോൺക്രീറ്റ് വസ്തുക്കൾ സൃഷ്ടിക്കുന്നതിന് ഫാക്ടറിയുടെ ജനറിക് ഇന്റർഫേസ് ഉപയോഗിക്കുകയും ചെയ്യുന്നു. ഈ ആന്തരിക ഫാക്ടറികളിൽ നിന്ന് ഏത് കോൺക്രീറ്റ് വസ്തുക്കൾ ലഭിക്കുന്നുവെന്ന് ക്ലയന്റിന് അറിയില്ല, കാരണം ഇത് അവരുടെ ഉൽപ്പന്നങ്ങളുടെ ജനറിക് ഇന്റർഫേസുകൾ മാത്രം ഉപയോഗിക്കുന്നു. ഫാക്ടറി ഇന്റർഫേസിൽ തുറന്നുകാണിക്കുന്ന രീതികളിൽ ഒബ്ജക്റ്റ് സൃഷ്ടിക്കൽ നടപ്പിലാക്കുന്നതിനാൽ ഈ പാറ്റേൺ ഒരു കൂട്ടം ഒബ്ജക്റ്റുകൾ അവയുടെ പൊതുവായ ഉപയോഗത്തിൽ നിന്ന് വേർതിരിക്കുകയും ഒബ്ജക്റ്റ് കോമ്പോസിഷനെ ആശ്രയിക്കുകയും ചെയ്യുന്നു.
അമൂർത്ത ഫാക്ടറി പാറ്റേൺ: അമൂർത്തമായ ഫാക്ടറി പാറ്റേൺ ഒരു കൂട്ടം വ്യക്തിഗത ഫാക്ടറികളുടെ കോൺക്രീറ്റ് ക്ലാസുകൾ വ്യക്തമാക്കാതെ ഒരു പൊതു തീം ഉൾക്കൊള്ളുന്ന ഒരു മാർഗ്ഗം ഉൾക്കൊള്ളുന്നു. സാധാരണ ഉപയോഗത്തിൽ, ക്ലയന്റ് സോഫ്റ്റ്വെയർ അമൂർത്ത ഫാക്ടറിയുടെ ഒരു ശക്തമായ നടപ്പാക്കൽ സൃഷ്ടിക്കുകയും തുടർന്ന് തീമിന്റെ ഭാഗമായ കോൺക്രീറ്റ് വസ്തുക്കൾ സൃഷ്ടിക്കുന്നതിന് ഫാക്ടറിയുടെ ജനറിക് ഇന്റർഫേസ് ഉപയോഗിക്കുകയും ചെയ്യുന്നു. ഈ ആന്തരിക ഫാക്ടറികളിൽ നിന്ന് ഏത് കോൺക്രീറ്റ് വസ്തുക്കൾ ലഭിക്കുന്നുവെന്ന് ക്ലയന്റിന് അറിയില്ല, കാരണം ഇത് അവരുടെ ഉൽപ്പന്നങ്ങളുടെ ജനറിക് ഇന്റർഫേസുകൾ മാത്രം ഉപയോഗിക്കുന്നു. ഫാക്ടറി ഇന്റർഫേസിൽ തുറന്നുകാണിക്കുന്ന രീതികളിൽ ഒബ്ജക്റ്റ് സൃഷ്ടിക്കൽ നടപ്പിലാക്കുന്നതിനാൽ ഈ പാറ്റേൺ ഒരു കൂട്ടം ഒബ്ജക്റ്റുകൾ അവയുടെ പൊതുവായ ഉപയോഗത്തിൽ നിന്ന് വേർതിരിക്കുകയും ഒബ്ജക്റ്റ് കോമ്പോസിഷനെ ആശ്രയിക്കുകയും ചെയ്യുന്നു.
സ്വീകർത്താക്കളുടെ അമൂർത്ത കുടുംബം: സാമാന്യവൽക്കരിച്ച സ്വീകർത്താക്കളുടെ ഒരു ഗ്രൂപ്പാണ് സ്വീകർത്താക്കളുടെ ഒരു അമൂർത്ത കുടുംബം (AFA) . അനൗപചാരികമായി, ഒരു സ്വീകർത്താവ് ഒരു പരിമിത സംസ്ഥാന നിയന്ത്രണമുള്ള ഒരു ഉപകരണമാണ്, പരിമിതമായ എണ്ണം ഇൻപുട്ട് ചിഹ്നങ്ങൾ, ഒരു റീഡ് ആൻഡ് റൈറ്റ് ഫംഗ്ഷൻ ഉള്ള ഒരു ആന്തരിക സ്റ്റോർ. ഓരോ സ്വീകർത്താവിനും ഒരു ആരംഭ സംസ്ഥാനവും ഒരു കൂട്ടം സ്വീകരിക്കുന്ന സംസ്ഥാനങ്ങളും ഉണ്ട്. ഓരോ ഇൻപുട്ട് ചിഹ്നത്തിനും ഉപകരണം ചിഹ്നങ്ങളുടെ ഒരു ശ്രേണി വായിക്കുന്നു. ഉപകരണം സ്വീകാര്യമായ അവസ്ഥയിൽ അവസാനിക്കുകയാണെങ്കിൽ, ഉപകരണം ചിഹ്നങ്ങളുടെ ക്രമം സ്വീകരിക്കുന്നതായി പറയപ്പെടുന്നു. ഒരേ തരത്തിലുള്ള ആന്തരിക സ്റ്റോറുള്ള സ്വീകർത്താക്കളുടെ ഒരു കൂട്ടമാണ് സ്വീകർത്താക്കളുടെ കുടുംബം. എ.എഫ്.എൽ സിദ്ധാന്തം എ.എഫ്.എൽ സിദ്ധാന്തത്തിന്റെ ഭാഗമാണ്.
ഭാഷകളുടെ അമൂർത്ത കുടുംബം: കമ്പ്യൂട്ടർ സയൻസിൽ, പ്രത്യേകിച്ചും formal പചാരിക ഭാഷാ സിദ്ധാന്തത്തിന്റെ മേഖലയിൽ, ഭാഷകളുടെ ഒരു അമൂർത്ത കുടുംബം എന്നത് സാധാരണ ഭാഷകൾക്കും സന്ദർഭരഹിതമായ ഭാഷകൾക്കും ആവർത്തിച്ചുള്ള എണ്ണമറ്റ ഭാഷകൾക്കും പഠിച്ച formal പചാരിക ഭാഷകളുടെ മറ്റ് കുടുംബങ്ങൾക്കും പൊതുവായുള്ള സവിശേഷതകളെ സാമാന്യവൽക്കരിക്കുന്ന ഒരു അമൂർത്ത ഗണിത സങ്കൽപ്പമാണ്. ശാസ്ത്രസാഹിത്യത്തിൽ.
നോൺ-നോറേറ്റീവ് ഫിലിം: നോൺ-നോറേറ്റീവ് ഫിലിം സിനിമാറ്റിക് ഫിലിമിന്റെ സൗന്ദര്യാത്മകമാണ്, അത് "ഒരു സംഭവത്തെ യഥാർത്ഥമോ സാങ്കൽപ്പികമോ" എന്ന് വിവരിക്കുകയോ വിവരിക്കുകയോ ഇല്ല. ഇത് സാധാരണയായി ഒരു കലാ ചലച്ചിത്രത്തിന്റെ അല്ലെങ്കിൽ പരീക്ഷണാത്മക സിനിമയാണ്, ഇത് ബഹുജന വിനോദത്തിനായി നിർമ്മിച്ചിട്ടില്ല.
നോൺ-നോറേറ്റീവ് ഫിലിം: നോൺ-നോറേറ്റീവ് ഫിലിം സിനിമാറ്റിക് ഫിലിമിന്റെ സൗന്ദര്യാത്മകമാണ്, അത് "ഒരു സംഭവത്തെ യഥാർത്ഥമോ സാങ്കൽപ്പികമോ" എന്ന് വിവരിക്കുകയോ വിവരിക്കുകയോ ഇല്ല. ഇത് സാധാരണയായി ഒരു കലാ ചലച്ചിത്രത്തിന്റെ അല്ലെങ്കിൽ പരീക്ഷണാത്മക സിനിമയാണ്, ഇത് ബഹുജന വിനോദത്തിനായി നിർമ്മിച്ചിട്ടില്ല.
സംഗ്രഹം: സംഗ്രഹം ഇനിപ്പറയുന്നവയെ പരാമർശിക്കാം: അബ്‌സ്ട്രാക്റ്റ് (ആൽബം) , ജോ ഹാരിയറ്റിന്റെ 1962 ആൽബം സംഗ്രഹം (നിയമം), ഒരു നിയമ പ്രമാണത്തിന്റെ സംഗ്രഹം അക്കാദമിക് പ്രസിദ്ധീകരണത്തിൽ സംഗ്രഹം (സംഗ്രഹം) അമൂർത്ത കല, യാഥാർത്ഥ്യത്തെയോ കോൺക്രീറ്റ് വിഷയങ്ങളെയോ പ്രതിനിധീകരിക്കാൻ ശ്രമിക്കാത്ത കലാസൃഷ്ടികൾ സംഗ്രഹം: ആർട്ട് ഓഫ് ഡിസൈൻ , 2017 നെറ്റ്ഫ്ലിക്സ് ഡോക്യുമെന്ററി സീരീസ് അമൂർത്ത സംഗീതം, പ്രാതിനിധ്യമില്ലാത്ത സംഗീതം തത്ത്വചിന്തയിലെ അമൂർത്തമായ വസ്‌തു ഗണിതത്തിലെ അമൂർത്ത ഘടന കമ്പ്യൂട്ടർ സയൻസിലെ അമൂർത്ത തരം ഒരു സംഗ്രഹത്തിന്റെ സ്വത്ത് ക്യൂ-ടിപ്പ് (സംഗീതജ്ഞൻ), "ദി അബ്‌സ്ട്രാക്റ്റ്" എന്നും അറിയപ്പെടുന്നു
അമൂർത്ത തന്ത്ര ഗെയിം: കളിയുടെ അനുഭവത്തിന് തീം പ്രധാനമല്ലാത്ത ഒരു തന്ത്ര ഗെയിമാണ് അമൂർത്ത തന്ത്ര ഗെയിം . ലോകത്തെ പല ക്ലാസിക് ബോർഡ് ഗെയിമുകളായ ചെസ്സ്, ഗോ, ചെക്കറുകളും ഡ്രാഫ്റ്റുകളും, സിയാങ്‌കി, ഷോഗി, റിവേർ‌സി, ഒൻപത് പുരുഷന്മാരുടെ മോറിസ്, മിക്ക മങ്കാല വേരിയന്റുകളും ഈ വിഭാഗത്തിൽ‌ ഉൾ‌പ്പെടുന്നു, ഡാമിയോ, ഹീവ്, യിൻ‌ഷ് എന്നിവപോലുള്ള ആധുനിക ആവർത്തനങ്ങൾ‌ പോലെ .
അമൂർത്ത ഗ്രാഫിക്കൽ ഡാറ്റ തരം: കമ്പ്യൂട്ടർ ഗ്രാഫിക്സിനായുള്ള ഒരു അമൂർത്ത ഡാറ്റാ തരത്തിന്റെ വിപുലീകരണമാണ് അമൂർത്ത ഗ്രാഫിക്കൽ ഡാറ്റ തരം ( എജിഡിടി ). എ.ജി.ഡി.ടികൾ എ.ഡി.ടികളുടെ ഗുണങ്ങൾ ഗ്രാഫിക്കൽ വസ്തുക്കൾ ഘടനാപരമായ രീതിയിൽ നിർമ്മിക്കാനുള്ള സൗകര്യങ്ങൾ നൽകുന്നു. G ദ്യോഗികമായി, ഒരു എജിഡിടിയെ "ഗ്രാഫിക്കൽ ഒബ്ജക്റ്റുകളുടെ ക്ലാസ്" എന്ന് നിർവചിക്കാം, അതിന്റെ ലോജിക്കൽ സ്വഭാവം ഒരു കൂട്ടം ഗ്രാഫിക്കൽ സ്വഭാവങ്ങളും ഒരു കൂട്ടം ഗ്രാഫിക്കൽ പ്രവർത്തനങ്ങളും നിർവചിക്കുന്നു.
ഗ്രൂപ്പ് സിദ്ധാന്തം: ഗണിതത്തിലും അമൂർത്ത ബീജഗണിതത്തിലും ഗ്രൂപ്പ് സിദ്ധാന്തം ഗ്രൂപ്പുകൾ എന്നറിയപ്പെടുന്ന ബീജഗണിത ഘടനകളെ പഠിക്കുന്നു. ഒരു ഗ്രൂപ്പിന്റെ ആശയം അമൂർത്ത ബീജഗണിതത്തിന്റെ കേന്ദ്രമാണ്: വളയങ്ങൾ, ഫീൽഡുകൾ, വെക്റ്റർ സ്പെയ്സുകൾ എന്നിവ പോലുള്ള മറ്റ് അറിയപ്പെടുന്ന ബീജഗണിത ഘടനകളെല്ലാം അധിക പ്രവർത്തനങ്ങളും പ്രപഞ്ചങ്ങളും ഉൾക്കൊള്ളുന്ന ഗ്രൂപ്പുകളായി കാണാൻ കഴിയും. ഗണിതത്തിലുടനീളം ഗ്രൂപ്പുകൾ ആവർത്തിക്കുന്നു, ഗ്രൂപ്പ് സിദ്ധാന്തത്തിന്റെ രീതികൾ ബീജഗണിതത്തിന്റെ പല ഭാഗങ്ങളെയും സ്വാധീനിച്ചിട്ടുണ്ട്. ലീനിയർ ബീജഗണിത ഗ്രൂപ്പുകളും ലീ ഗ്രൂപ്പുകളും ഗ്രൂപ്പ് സിദ്ധാന്തത്തിന്റെ രണ്ട് ശാഖകളാണ്, അവ മുന്നേറ്റങ്ങൾ അനുഭവിക്കുകയും അവരുടേതായ വിഷയ മേഖലകളായി മാറുകയും ചെയ്തു.
ഹാർമോണിക് വിശകലനം: അടിസ്ഥാന തരംഗങ്ങളുടെ സൂപ്പർപോസിഷനായി ഫംഗ്ഷനുകളെയോ സിഗ്നലുകളെയോ പ്രതിനിധീകരിക്കുന്നതുമായി ബന്ധപ്പെട്ട ഗണിതശാസ്ത്രത്തിന്റെ ഒരു ശാഖയാണ് ഹാർമോണിക് വിശകലനം , കൂടാതെ ഫ്യൂറിയർ സീരീസ്, ഫൂറിയർ ട്രാൻസ്ഫോർമുകൾ എന്നിവയുടെ പഠനങ്ങളും സാമാന്യവൽക്കരണവും. കഴിഞ്ഞ രണ്ട് നൂറ്റാണ്ടുകളിൽ, നമ്പർ തിയറി, പ്രാതിനിധ്യ സിദ്ധാന്തം, സിഗ്നൽ പ്രോസസ്സിംഗ്, ക്വാണ്ടം മെക്കാനിക്സ്, ടൈഡൽ അനാലിസിസ്, ന്യൂറോ സയൻസ് എന്നിങ്ങനെ വൈവിധ്യമാർന്ന മേഖലകളിലെ പ്രയോഗങ്ങളുള്ള ഒരു വിശാലമായ വിഷയമായി ഇത് മാറിയിരിക്കുന്നു.
ഇതര ഹിപ് ഹോപ്പ്: മുഖ്യധാരയായി സാധാരണ തിരിച്ചറിയപ്പെടാത്ത വൈവിധ്യമാർന്ന ശൈലികൾ ഉൾക്കൊള്ളുന്ന ഹിപ് ഹോപ്പ് സംഗീതത്തിന്റെ ഉപവിഭാഗമാണ് ഇതര ഹിപ് ഹോപ്പ് . ഓൾ‌ മ്യൂസിക് ഇതിനെ ഇനിപ്പറയുന്ന രീതിയിൽ നിർ‌വ്വചിക്കുന്നു: "റാങ്‌സിന്റെ പരമ്പരാഗത സ്റ്റീരിയോടൈപ്പുകളായ ഗ്യാങ്‌സ്റ്റ, ബാസ്, ഹാർഡ്‌കോർ, പോപ്പ്, പാർട്ടി റാപ്പ് എന്നിവയുമായി പൊരുത്തപ്പെടാൻ വിസമ്മതിക്കുന്ന ഹിപ് ഹോപ്പ് ഗ്രൂപ്പുകളെയാണ് ഇതര റാപ്പ് എന്ന് പറയുന്നത്. പകരം, ഫങ്കിൽ നിന്ന് തുല്യമായി വരയ്ക്കുന്ന വിഭാഗങ്ങളെ അവ്യക്തമാക്കുന്നു. പോപ്പ് / റോക്ക്, ജാസ്, സോൾ, റെഗ്ഗെ, നാടോടി എന്നിവയും.
ഇതര ഹിപ് ഹോപ്പ്: മുഖ്യധാരയായി സാധാരണ തിരിച്ചറിയപ്പെടാത്ത വൈവിധ്യമാർന്ന ശൈലികൾ ഉൾക്കൊള്ളുന്ന ഹിപ് ഹോപ്പ് സംഗീതത്തിന്റെ ഉപവിഭാഗമാണ് ഇതര ഹിപ് ഹോപ്പ് . ഓൾ‌ മ്യൂസിക് ഇതിനെ ഇനിപ്പറയുന്ന രീതിയിൽ നിർ‌വ്വചിക്കുന്നു: "റാങ്‌സിന്റെ പരമ്പരാഗത സ്റ്റീരിയോടൈപ്പുകളായ ഗ്യാങ്‌സ്റ്റ, ബാസ്, ഹാർഡ്‌കോർ, പോപ്പ്, പാർട്ടി റാപ്പ് എന്നിവയുമായി പൊരുത്തപ്പെടാൻ വിസമ്മതിക്കുന്ന ഹിപ് ഹോപ്പ് ഗ്രൂപ്പുകളെയാണ് ഇതര റാപ്പ് എന്ന് പറയുന്നത്. പകരം, ഫങ്കിൽ നിന്ന് തുല്യമായി വരയ്ക്കുന്ന വിഭാഗങ്ങളെ അവ്യക്തമാക്കുന്നു. പോപ്പ് / റോക്ക്, ജാസ്, സോൾ, റെഗ്ഗെ, നാടോടി എന്നിവയും.
ഇതര ഹിപ് ഹോപ്പ്: മുഖ്യധാരയായി സാധാരണ തിരിച്ചറിയപ്പെടാത്ത വൈവിധ്യമാർന്ന ശൈലികൾ ഉൾക്കൊള്ളുന്ന ഹിപ് ഹോപ്പ് സംഗീതത്തിന്റെ ഉപവിഭാഗമാണ് ഇതര ഹിപ് ഹോപ്പ് . ഓൾ‌ മ്യൂസിക് ഇതിനെ ഇനിപ്പറയുന്ന രീതിയിൽ നിർ‌വ്വചിക്കുന്നു: "റാങ്‌സിന്റെ പരമ്പരാഗത സ്റ്റീരിയോടൈപ്പുകളായ ഗ്യാങ്‌സ്റ്റ, ബാസ്, ഹാർഡ്‌കോർ, പോപ്പ്, പാർട്ടി റാപ്പ് എന്നിവയുമായി പൊരുത്തപ്പെടാൻ വിസമ്മതിക്കുന്ന ഹിപ് ഹോപ്പ് ഗ്രൂപ്പുകളെയാണ് ഇതര റാപ്പ് എന്ന് പറയുന്നത്. പകരം, ഫങ്കിൽ നിന്ന് തുല്യമായി വരയ്ക്കുന്ന വിഭാഗങ്ങളെ അവ്യക്തമാക്കുന്നു. പോപ്പ് / റോക്ക്, ജാസ്, സോൾ, റെഗ്ഗെ, നാടോടി എന്നിവയും.
ഹോമോടോപ്പി സിദ്ധാന്തം: ഗണിതശാസ്ത്രത്തിൽ, മാപ്പുകൾ അവയ്ക്കിടയിൽ ഹോമോടോപ്പികളുമായി വരുന്ന സാഹചര്യങ്ങളെക്കുറിച്ചുള്ള ആസൂത്രിതമായ പഠനമാണ് ഹോമോടോപ്പി സിദ്ധാന്തം . ബീജഗണിത ടോപ്പോളജിയിലെ ഒരു വിഷയമായിട്ടാണ് ഇത് ഉത്ഭവിച്ചത്, എന്നാൽ ഇപ്പോൾ ഇത് ഒരു സ്വതന്ത്ര ശിക്ഷണമായി പഠിക്കപ്പെടുന്നു. ബീജഗണിത ടോപ്പോളജി കൂടാതെ, ഗണിതത്തിലെ മറ്റ് മേഖലകളായ ബീജഗണിത ജ്യാമിതി (ഉദാ. എ 1 ഹോമോടോപ്പി സിദ്ധാന്തം ), കാറ്റഗറി തിയറി (പ്രത്യേകിച്ചും ഉയർന്ന വിഭാഗങ്ങളെക്കുറിച്ചുള്ള പഠനം) എന്നിവയിലും ഈ സിദ്ധാന്തം ഉപയോഗിച്ചിട്ടുണ്ട്.
അമൂർത്ത മിഥ്യാധാരണ: 1967 ൽ കലാചരിത്രകാരിയും നിരൂപകനുമായ ബാർബറ റോസ് ആവിഷ്‌കരിച്ച അബ്‌സ്ട്രാക്റ്റ് മായവാദം. 1970 കളുടെ മധ്യത്തിൽ അമേരിക്കയിൽ പ്രചാരത്തിലുണ്ടായ ഒരു കലാപരമായ പ്രസ്ഥാനത്തെ നിർവചിക്കാൻ ലൂയിസ് കെ. മീസൽ സ്വതന്ത്രമായി ഈ പദം ഉപയോഗിച്ചു.
അമൂർത്ത കല: ലോകത്തിലെ വിഷ്വൽ റഫറൻസുകളിൽ നിന്ന് ഒരു പരിധിവരെ സ്വാതന്ത്ര്യത്തോടുകൂടിയ ഒരു രചന സൃഷ്ടിക്കാൻ അമൂർത്ത കല രൂപം, രൂപം, നിറം, രേഖ എന്നിവയുടെ വിഷ്വൽ ഭാഷ ഉപയോഗിക്കുന്നു. പാശ്ചാത്യ കല, നവോത്ഥാനം മുതൽ പത്തൊൻപതാം നൂറ്റാണ്ടിന്റെ മദ്ധ്യകാലം വരെ, കാഴ്ചപ്പാടിന്റെ യുക്തിയും ദൃശ്യമായ യാഥാർത്ഥ്യത്തിന്റെ ഒരു മിഥ്യാധാരണയെ പുനർനിർമ്മിക്കാനുള്ള ശ്രമവുമാണ്. പത്തൊൻപതാം നൂറ്റാണ്ടിന്റെ അവസാനത്തോടെ സാങ്കേതികവിദ്യ, ശാസ്ത്രം, തത്ത്വചിന്ത എന്നിവയിൽ സംഭവിക്കുന്ന അടിസ്ഥാനപരമായ മാറ്റങ്ങൾ ഉൾക്കൊള്ളുന്ന ഒരു പുതിയ തരം കല സൃഷ്ടിക്കേണ്ടതുണ്ടെന്ന് പല കലാകാരന്മാർക്കും തോന്നി. വ്യക്തിഗത കലാകാരന്മാർ അവരുടെ സൈദ്ധാന്തിക വാദങ്ങൾ ഉന്നയിച്ച ഉറവിടങ്ങൾ വൈവിധ്യപൂർണ്ണമായിരുന്നു, അക്കാലത്ത് പാശ്ചാത്യ സംസ്കാരത്തിന്റെ എല്ലാ മേഖലകളിലെയും സാമൂഹികവും ബ ual ദ്ധികവുമായ മുൻ‌തൂക്കങ്ങൾ പ്രതിഫലിപ്പിച്ചു.
അമൂർത്ത ഇമാജിസ്റ്റുകൾ: 1961 ൽ ​​ന്യൂയോർക്കിലെ ഗുഗ്ഗൻഹൈം മ്യൂസിയത്തിൽ നടന്ന ഒരു എക്സിബിഷനിൽ നിന്ന് അമേരിക്കൻ അബ്‌സ്ട്രാക്റ്റ് എക്‌സ്‌പ്രഷനിസ്റ്റുകളും ഇമാജിസ്റ്റുകളും എന്ന പദത്തിൽ നിന്നാണ് ഉരുത്തിരിഞ്ഞത് . അമേരിക്കൻ, യൂറോപ്യൻ പെയിന്റിംഗ്, ശില്പം എന്നിവയിലെ പ്രവണതകളെക്കുറിച്ച് അന്വേഷിക്കുന്നതിനുള്ള പ്രോഗ്രാമുകളുടെ പരമ്പരയിലെ ആദ്യത്തേതാണ് ഈ എക്സിബിഷൻ.
അമൂർത്ത ഇമാജിസ്റ്റുകൾ: 1961 ൽ ​​ന്യൂയോർക്കിലെ ഗുഗ്ഗൻഹൈം മ്യൂസിയത്തിൽ നടന്ന ഒരു എക്സിബിഷനിൽ നിന്ന് അമേരിക്കൻ അബ്‌സ്ട്രാക്റ്റ് എക്‌സ്‌പ്രഷനിസ്റ്റുകളും ഇമാജിസ്റ്റുകളും എന്ന പദത്തിൽ നിന്നാണ് ഉരുത്തിരിഞ്ഞത് . അമേരിക്കൻ, യൂറോപ്യൻ പെയിന്റിംഗ്, ശില്പം എന്നിവയിലെ പ്രവണതകളെക്കുറിച്ച് അന്വേഷിക്കുന്നതിനുള്ള പ്രോഗ്രാമുകളുടെ പരമ്പരയിലെ ആദ്യത്തേതാണ് ഈ എക്സിബിഷൻ.
അമൂർത്ത ഇംപ്രഷനിസം: 1940 കളിൽ ന്യൂയോർക്ക് സിറ്റിയിൽ ആരംഭിച്ച ഒരു കലാ പ്രസ്ഥാനമാണ് അമൂർത്ത ഇംപ്രഷനിസം . ഇംപ്രഷനിസ്റ്റ് ശൈലിയിൽ യഥാർത്ഥ ജീവിത രംഗങ്ങൾ, വസ്തുക്കൾ അല്ലെങ്കിൽ ആളുകൾ (ഛായാചിത്രങ്ങൾ) പോലുള്ള ഒരു വിഷയത്തിന്റെ പെയിന്റിംഗ് ഇതിൽ ഉൾപ്പെടുന്നു, എന്നാൽ വ്യത്യസ്ത അമൂർത്ത നടപടികൾക്ക് emphas ന്നൽ നൽകുന്നു. പെയിന്റിംഗുകൾ പലപ്പോഴും പെയിന്റ് ചെയ്യുന്നത് എൻ പ്ലെയിൻ എയർ ആണ്, ആർട്ടിസ്റ്റിന് മുന്നിൽ ലാൻഡ്സ്കേപ്പിനൊപ്പം നേരിട്ട് പെയിന്റിംഗ് ഉൾപ്പെടുന്ന ഒരു കലാപരമായ ശൈലി. ശുദ്ധമായ അമൂർത്തതയുടെ വരകൾക്കും പെയിന്റിംഗിലെ യാഥാർത്ഥ്യത്തിന്റെ ഒരു അലവൻസ് അലവൻസുകൾക്കുമിടയിൽ ഈ ചലനം അതിമനോഹരമായി പ്രവർത്തിക്കുന്നു.
അമൂർത്ത ഇംപ്രഷനിസം: 1940 കളിൽ ന്യൂയോർക്ക് സിറ്റിയിൽ ആരംഭിച്ച ഒരു കലാ പ്രസ്ഥാനമാണ് അമൂർത്ത ഇംപ്രഷനിസം . ഇംപ്രഷനിസ്റ്റ് ശൈലിയിൽ യഥാർത്ഥ ജീവിത രംഗങ്ങൾ, വസ്തുക്കൾ അല്ലെങ്കിൽ ആളുകൾ (ഛായാചിത്രങ്ങൾ) പോലുള്ള ഒരു വിഷയത്തിന്റെ പെയിന്റിംഗ് ഇതിൽ ഉൾപ്പെടുന്നു, എന്നാൽ വ്യത്യസ്ത അമൂർത്ത നടപടികൾക്ക് emphas ന്നൽ നൽകുന്നു. പെയിന്റിംഗുകൾ പലപ്പോഴും പെയിന്റ് ചെയ്യുന്നത് എൻ പ്ലെയിൻ എയർ ആണ്, ആർട്ടിസ്റ്റിന് മുന്നിൽ ലാൻഡ്സ്കേപ്പിനൊപ്പം നേരിട്ട് പെയിന്റിംഗ് ഉൾപ്പെടുന്ന ഒരു കലാപരമായ ശൈലി. ശുദ്ധമായ അമൂർത്തതയുടെ വരകൾക്കും പെയിന്റിംഗിലെ യാഥാർത്ഥ്യത്തിന്റെ ഒരു അലവൻസ് അലവൻസുകൾക്കുമിടയിൽ ഈ ചലനം അതിമനോഹരമായി പ്രവർത്തിക്കുന്നു.
അമൂർത്ത സൂചിക നൊട്ടേഷൻ: ഒരു പ്രത്യേക അടിസ്ഥാനത്തിൽ അവയുടെ ഘടകങ്ങളേക്കാൾ അവയുടെ തരം സൂചിപ്പിക്കുന്നതിന് സൂചികകൾ ഉപയോഗിക്കുന്ന ടെൻസറുകൾക്കും സ്പിന്നർമാർക്കും വേണ്ടിയുള്ള ഒരു ഗണിതശാസ്ത്ര നൊട്ടേഷനാണ് അമൂർത്ത സൂചിക നൊട്ടേഷൻ . സൂചികകൾ കേവലം പ്ലെയ്‌സ്‌ഹോൾഡറുകളാണ്, അവ ഏതെങ്കിലും അടിസ്ഥാനവുമായി ബന്ധമില്ലാത്തതും പ്രത്യേകിച്ചും അക്കങ്ങളല്ലാത്തതുമാണ്. അതിനാൽ ഇത് റിച്ചി കാൽക്കുലസുമായി തെറ്റിദ്ധരിക്കരുത്. ആധുനിക അമൂർത്ത ടെൻസർ നൊട്ടേഷനിലെ സങ്കോചങ്ങളും കോവിയറന്റ് ഡിഫറൻസേഷനും വിവരിക്കുന്നതിലെ ബുദ്ധിമുട്ട് നികത്താൻ ഐൻ‌സ്റ്റൈൻ സമ്മേഷൻ കൺവെൻഷന്റെ formal പചാരിക വശങ്ങൾ ഉപയോഗിക്കുന്നതിനുള്ള ഒരു മാർഗമായി റോജർ പെൻറോസ് ഈ നൊട്ടേഷൻ അവതരിപ്പിച്ചു.
സൂചിക ഗ്രൂപ്പ്: ഗണിതശാസ്ത്ര ശാഖയായ ഓപ്പറേറ്റർ സിദ്ധാന്തത്തിൽ, ഓരോ ബനാച്ച് ആൾജിബ്രയെയും അതിന്റെ അമൂർത്ത സൂചിക ഗ്രൂപ്പ് എന്ന് വിളിക്കുന്ന ഒരു ഗ്രൂപ്പുമായി ബന്ധപ്പെടുത്താം.
അമൂർത്ത സൂചിക നൊട്ടേഷൻ: ഒരു പ്രത്യേക അടിസ്ഥാനത്തിൽ അവയുടെ ഘടകങ്ങളേക്കാൾ അവയുടെ തരം സൂചിപ്പിക്കുന്നതിന് സൂചികകൾ ഉപയോഗിക്കുന്ന ടെൻസറുകൾക്കും സ്പിന്നർമാർക്കും വേണ്ടിയുള്ള ഒരു ഗണിതശാസ്ത്ര നൊട്ടേഷനാണ് അമൂർത്ത സൂചിക നൊട്ടേഷൻ . സൂചികകൾ കേവലം പ്ലെയ്‌സ്‌ഹോൾഡറുകളാണ്, അവ ഏതെങ്കിലും അടിസ്ഥാനവുമായി ബന്ധമില്ലാത്തതും പ്രത്യേകിച്ചും അക്കങ്ങളല്ലാത്തതുമാണ്. അതിനാൽ ഇത് റിച്ചി കാൽക്കുലസുമായി തെറ്റിദ്ധരിക്കരുത്. ആധുനിക അമൂർത്ത ടെൻസർ നൊട്ടേഷനിലെ സങ്കോചങ്ങളും കോവിയറന്റ് ഡിഫറൻസേഷനും വിവരിക്കുന്നതിലെ ബുദ്ധിമുട്ട് നികത്താൻ ഐൻ‌സ്റ്റൈൻ സമ്മേഷൻ കൺവെൻഷന്റെ formal പചാരിക വശങ്ങൾ ഉപയോഗിക്കുന്നതിനുള്ള ഒരു മാർഗമായി റോജർ പെൻറോസ് ഈ നൊട്ടേഷൻ അവതരിപ്പിച്ചു.
അമൂർത്ത സൂചിക നൊട്ടേഷൻ: ഒരു പ്രത്യേക അടിസ്ഥാനത്തിൽ അവയുടെ ഘടകങ്ങളേക്കാൾ അവയുടെ തരം സൂചിപ്പിക്കുന്നതിന് സൂചികകൾ ഉപയോഗിക്കുന്ന ടെൻസറുകൾക്കും സ്പിന്നർമാർക്കും വേണ്ടിയുള്ള ഒരു ഗണിതശാസ്ത്ര നൊട്ടേഷനാണ് അമൂർത്ത സൂചിക നൊട്ടേഷൻ . സൂചികകൾ കേവലം പ്ലെയ്‌സ്‌ഹോൾഡറുകളാണ്, അവ ഏതെങ്കിലും അടിസ്ഥാനവുമായി ബന്ധമില്ലാത്തതും പ്രത്യേകിച്ചും അക്കങ്ങളല്ലാത്തതുമാണ്. അതിനാൽ ഇത് റിച്ചി കാൽക്കുലസുമായി തെറ്റിദ്ധരിക്കരുത്. ആധുനിക അമൂർത്ത ടെൻസർ നൊട്ടേഷനിലെ സങ്കോചങ്ങളും കോവിയറന്റ് ഡിഫറൻസേഷനും വിവരിക്കുന്നതിലെ ബുദ്ധിമുട്ട് നികത്താൻ ഐൻ‌സ്റ്റൈൻ സമ്മേഷൻ കൺവെൻഷന്റെ formal പചാരിക വശങ്ങൾ ഉപയോഗിക്കുന്നതിനുള്ള ഒരു മാർഗമായി റോജർ പെൻറോസ് ഈ നൊട്ടേഷൻ അവതരിപ്പിച്ചു.
ഇന്റലിജന്റ് ഏജന്റ്: ആർട്ടിഫിഷ്യൽ ഇന്റലിജൻസിൽ, ഇന്റലിജന്റ് ഏജന്റ് ( ഐ‌എ ) ഒരു സ്വയംഭരണ സ്ഥാപനത്തെ സൂചിപ്പിക്കുന്നു, അത് സെൻസറുകളിലൂടെയും അനന്തരഫലമായ ആക്യുവേറ്ററുകളിലൂടെയും നിരീക്ഷണം ഉപയോഗിക്കുന്ന ഒരു പരിതസ്ഥിതിയിൽ, ലക്ഷ്യങ്ങൾ കൈവരിക്കുന്നതിനായി അതിന്റെ പ്രവർത്തനത്തെ നയിക്കുന്നു. ഇന്റലിജന്റ് ഏജന്റുമാർ അവരുടെ ലക്ഷ്യങ്ങൾ നേടുന്നതിന് അറിവ് പഠിക്കുകയോ ഉപയോഗിക്കുകയോ ചെയ്യാം. അവ വളരെ ലളിതമോ സങ്കീർണ്ണമോ ആകാം. ഒരു തെർമോസ്റ്റാറ്റ് പോലുള്ള ഒരു റിഫ്ലെക്സ് മെഷീൻ ഒരു ബുദ്ധിമാനായ ഏജന്റിന്റെ ഉദാഹരണമായി കണക്കാക്കപ്പെടുന്നു.
അമൂർത്ത പാളി: കമ്പ്യൂട്ടിംഗിൽ, ഒരു സബ്സിസ്റ്റത്തിന്റെ പ്രവർത്തന വിശദാംശങ്ങൾ മറയ്ക്കുന്നതിനുള്ള ഒരു മാർഗമാണ് അമൂർത്ത പാളി അല്ലെങ്കിൽ അമൂർത്ത നില . നെറ്റ്വർക്ക് പ്രോട്ടോക്കോളുകൾ, ഓപ്പൺജിഎൽ, മറ്റ് ഗ്രാഫിക്സ് ലൈബ്രറികൾ എന്നിവയ്ക്കുള്ള ഒഎസ്ഐ മോഡൽ അമൂർത്തത്തിന്റെ പാളികൾ ഉപയോഗിക്കുന്ന സോഫ്റ്റ്വെയർ മോഡലുകളുടെ ഉദാഹരണങ്ങളിൽ ഉൾപ്പെടുന്നു.
അമൂർത്ത വ്യാഖ്യാനം: കമ്പ്യൂട്ടർ സയൻസിൽ, ഓർഡർ ചെയ്ത സെറ്റുകളിൽ, പ്രത്യേകിച്ച് ലാറ്റിസുകളിൽ മോണോടോണിക് ഫംഗ്ഷനുകളെ അടിസ്ഥാനമാക്കി കമ്പ്യൂട്ടർ പ്രോഗ്രാമുകളുടെ സെമാന്റിക്സിന്റെ ശബ്ദ ഏകദേശ സിദ്ധാന്തമാണ് അമൂർത്ത വ്യാഖ്യാനം . എല്ലാ കണക്കുകൂട്ടലുകളും നടത്താതെ തന്നെ അതിന്റെ അർത്ഥശാസ്ത്രത്തെക്കുറിച്ചുള്ള വിവരങ്ങൾ നേടുന്ന ഒരു കമ്പ്യൂട്ടർ പ്രോഗ്രാമിന്റെ ഭാഗിക നിർവ്വഹണമായി ഇതിനെ കാണാൻ കഴിയും.
അമൂർത്ത വ്യാഖ്യാനം: കമ്പ്യൂട്ടർ സയൻസിൽ, ഓർഡർ ചെയ്ത സെറ്റുകളിൽ, പ്രത്യേകിച്ച് ലാറ്റിസുകളിൽ മോണോടോണിക് ഫംഗ്ഷനുകളെ അടിസ്ഥാനമാക്കി കമ്പ്യൂട്ടർ പ്രോഗ്രാമുകളുടെ സെമാന്റിക്സിന്റെ ശബ്ദ ഏകദേശ സിദ്ധാന്തമാണ് അമൂർത്ത വ്യാഖ്യാനം . എല്ലാ കണക്കുകൂട്ടലുകളും നടത്താതെ തന്നെ അതിന്റെ അർത്ഥശാസ്ത്രത്തെക്കുറിച്ചുള്ള വിവരങ്ങൾ നേടുന്ന ഒരു കമ്പ്യൂട്ടർ പ്രോഗ്രാമിന്റെ ഭാഗിക നിർവ്വഹണമായി ഇതിനെ കാണാൻ കഴിയും.
അമൂർത്ത അധ്വാനവും കോൺക്രീറ്റ് അധ്വാനവും: രാഷ്ട്രീയ സമ്പദ്‌വ്യവസ്ഥയെ വിമർശിക്കുന്നതിൽ കാൾ മാർക്സ് നടത്തിയ വേർതിരിവാണ് അമൂർത്ത അധ്വാനവും കോൺക്രീറ്റ് അധ്വാനവും സൂചിപ്പിക്കുന്നത്. ഒരു പ്രത്യേക ഉപയോഗപ്രദമായ ഫലമുണ്ടാക്കുന്ന ഒരു പ്രത്യേക പ്രവർത്തനമെന്ന നിലയിൽ പൊതുവെ മനുഷ്യ അധ്വാനം സാമ്പത്തികമായി മൂല്യവത്തായ ജോലിസമയവും മനുഷ്യ അധ്വാനവും തമ്മിലുള്ള വ്യത്യാസത്തെ ഇത് സൂചിപ്പിക്കുന്നു.
അമൂർത്ത അധ്വാനവും കോൺക്രീറ്റ് അധ്വാനവും: രാഷ്ട്രീയ സമ്പദ്‌വ്യവസ്ഥയെ വിമർശിക്കുന്നതിൽ കാൾ മാർക്സ് നടത്തിയ വേർതിരിവാണ് അമൂർത്ത അധ്വാനവും കോൺക്രീറ്റ് അധ്വാനവും സൂചിപ്പിക്കുന്നത്. ഒരു പ്രത്യേക ഉപയോഗപ്രദമായ ഫലമുണ്ടാക്കുന്ന ഒരു പ്രത്യേക പ്രവർത്തനമെന്ന നിലയിൽ പൊതുവെ മനുഷ്യ അധ്വാനം സാമ്പത്തികമായി മൂല്യവത്തായ ജോലിസമയവും മനുഷ്യ അധ്വാനവും തമ്മിലുള്ള വ്യത്യാസത്തെ ഇത് സൂചിപ്പിക്കുന്നു.
അമൂർത്ത അധ്വാനവും കോൺക്രീറ്റ് അധ്വാനവും: രാഷ്ട്രീയ സമ്പദ്‌വ്യവസ്ഥയെ വിമർശിക്കുന്നതിൽ കാൾ മാർക്സ് നടത്തിയ വേർതിരിവാണ് അമൂർത്ത അധ്വാനവും കോൺക്രീറ്റ് അധ്വാനവും സൂചിപ്പിക്കുന്നത്. ഒരു പ്രത്യേക ഉപയോഗപ്രദമായ ഫലമുണ്ടാക്കുന്ന ഒരു പ്രത്യേക പ്രവർത്തനമെന്ന നിലയിൽ പൊതുവെ മനുഷ്യ അധ്വാനം സാമ്പത്തികമായി മൂല്യവത്തായ ജോലിസമയവും മനുഷ്യ അധ്വാനവും തമ്മിലുള്ള വ്യത്യാസത്തെ ഇത് സൂചിപ്പിക്കുന്നു.
അമൂർത്ത യുക്തി: ഗണിതശാസ്ത്ര യുക്തിയിൽ, ഒരു തരം വാക്യങ്ങളും സംഭവം, വികാസം, ഐസോമോറിസം, പേരുമാറ്റൽ, അളവ് എന്നിവയുമായി ബന്ധപ്പെട്ട പ്രത്യേക സവിശേഷതകളുമായുള്ള സംതൃപ്തി ബന്ധവും ഉൾക്കൊള്ളുന്ന ഒരു system പചാരിക സംവിധാനമാണ് അമൂർത്ത യുക്തി .
അമൂർത്ത യുക്തി (വ്യതിചലനം): ഒരു കൂട്ടം വാക്യങ്ങളും നിർദ്ദിഷ്ട സവിശേഷതകളുമായുള്ള സംതൃപ്തി ബന്ധവും അടങ്ങുന്ന formal പചാരിക സംവിധാനമാണ് അമൂർത്ത യുക്തി .
അമൂർത്തമായ എം-സ്പേസ്: ഗണിതശാസ്ത്രത്തിൽ, പ്രത്യേകിച്ചും ഓർഡർ തിയറിയിലും ഫംഗ്ഷണൽ വിശകലനത്തിലും, ഒരു അമൂർത്തമായ എം- സ്പേസ് അല്ലെങ്കിൽ എഎം-സ്പേസ് ഒരു ബനാച്ച് ലാറ്റിസ് ആണ് ആരുടെ മാനദണ്ഡം തൃപ്തിപ്പെടുത്തുന്നു X ന്റെ പോസിറ്റീവ് കോണിലെ എല്ലാ x , y എന്നിവയ്ക്കും. ഇടവേളയിൽ [- u , u ]: = { z ∈ X : - u ≤ z , z that എന്നിങ്ങനെ X- ൽ കുറച്ച് u ≥ 0 ഉണ്ടെങ്കിൽ, AM- സ്‌പേസ് X എന്നത് യൂണിറ്റുള്ള AM- സ്‌പെയ്‌സ് ആണെന്ന് ഞങ്ങൾ പറയുന്നു. u X എന്നത് X ന്റെ യൂണിറ്റ് ബോളിന് തുല്യമാണ്; അത്തരമൊരു ഘടകം യു അദ്വിതീയവും എക്‌സിന്റെ ഓർഡർ യൂണിറ്റുമാണ്.
അമൂർത്ത യന്ത്രം: ഒരു അമൂർത്ത കമ്പ്യൂട്ടർ എന്നും വിളിക്കപ്പെടുന്ന ഒരു അമൂർത്ത യന്ത്രം ഒരു കമ്പ്യൂട്ടർ മാതൃക നിർവചിക്കാൻ ഉപയോഗിക്കുന്ന ഒരു സൈദ്ധാന്തിക കമ്പ്യൂട്ടറാണ്. കമ്പ്യൂട്ടർ സയൻസ്, കമ്പ്യൂട്ടർ എഞ്ചിനീയറിംഗ് വിഭാഗങ്ങളിൽ കമ്പ്യൂട്ടിംഗ് പ്രക്രിയകളുടെ സംഗ്രഹം ഉപയോഗിക്കുന്നു, മാത്രമല്ല ഇത് ഒരു പ്രത്യേക സമയ മാതൃകയെ കണക്കാക്കുന്നു.
ബി രീതി: കമ്പ്യൂട്ടർ സോഫ്റ്റ്വെയറിന്റെ വികസനത്തിന് ഉപയോഗിക്കുന്ന ഒരു അമൂർത്ത മെഷീൻ നൊട്ടേഷനെ അടിസ്ഥാനമാക്കിയുള്ള ഉപകരണ-പിന്തുണയുള്ള formal പചാരിക രീതിയായ ബി അടിസ്ഥാനമാക്കിയുള്ള സോഫ്റ്റ്വെയർ വികസന രീതിയാണ് ബി രീതി . 1980 കളിൽ ഫ്രാൻസിലും യുകെയിലും ജീൻ-റെയ്മണ്ട് അബ്രിയൽ ഇത് വികസിപ്പിച്ചെടുത്തു. ബി ഇസഡ് നൊട്ടേഷനുമായി ബന്ധപ്പെട്ടതാണ് കൂടാതെ സവിശേഷതകളിൽ നിന്ന് പ്രോഗ്രാമിംഗ് ഭാഷാ കോഡ് വികസിപ്പിക്കുന്നതിനെ പിന്തുണയ്ക്കുന്നു. യൂറോപ്പിലെ പ്രധാന സുരക്ഷാ-നിർണായക സിസ്റ്റം ആപ്ലിക്കേഷനുകളിൽ ബി ഉപയോഗിച്ചു. സ്‌പെസിഫിക്കേഷൻ, ഡിസൈൻ, പ്രൂഫ്, കോഡ് ജനറേഷൻ എന്നിവയ്‌ക്കായി ഇതിന് ശക്തമായ, വാണിജ്യപരമായി ലഭ്യമായ ഉപകരണ പിന്തുണയുണ്ട്.
അമൂർത്ത മാനേജുമെന്റ്: ഒരു അക്കാദമിക് കോൺഫറൻസിൽ അവതരണത്തിനായി സംഗ്രഹങ്ങൾ സ്വീകരിക്കുകയും തയ്യാറാക്കുകയും ചെയ്യുന്ന പ്രക്രിയയാണ് അമൂർത്ത മാനേജുമെന്റ് . ജോലിയുടെ അമൂർത്തമായ അല്ലെങ്കിൽ സംഗ്രഹത്തിന്റെ ക്ഷണിക്കപ്പെട്ട അല്ലെങ്കിൽ ലാഭകരമായ സമർപ്പിക്കലുകൾ ഈ പ്രക്രിയയിൽ അടങ്ങിയിരിക്കുന്നു. സംക്ഷിപ്തം, ഗവേഷണത്തിലോ അന്വേഷണത്തിലോ ഉപയോഗിക്കുന്ന ഉപകരണങ്ങൾ, ശേഖരിച്ച ഡാറ്റ, ഡാറ്റയുടെ സംഗ്രഹം അല്ലെങ്കിൽ വ്യാഖ്യാനം എന്നിവ അമൂർത്തത്തിൽ സാധാരണ പറയുന്നു.
മാനിഫോൾഡ്: ഗണിതശാസ്ത്രത്തിൽ, ഓരോ പോയിന്റിനും സമീപമുള്ള യൂക്ലിഡിയൻ സ്ഥലവുമായി പ്രാദേശികമായി സാമ്യമുള്ള ഒരു ടോപ്പോളജിക്കൽ സ്പേസ് ആണ് മാനിഫോൾഡ് . കൂടുതൽ കൃത്യമായി, ഒരു n -ദിമെംസിഒനല് പലമടങ്ങ്, അല്ലെങ്കിൽ n ചുരുക്കത്തിൽ -മനിഫൊല്ദ്, ഓരോ പോയിന്റ് അളവിനും എന്ന യൂക്ലിഡിയൻ വരെ ഹൊമെഒമൊര്ഫിച് n ലേക്കുള്ള സമീപസ്ഥലങ്ങൾ ഉണ്ടെന്ന് പ്രോപ്പർട്ടി ഗുണനവും സ്ഥലം.
ശുദ്ധമായ ഗണിതശാസ്ത്രം: ഗണിതശാസ്ത്രത്തിന് പുറത്തുള്ള ഏതൊരു ആപ്ലിക്കേഷനിൽ നിന്നും സ്വതന്ത്രമായി ഗണിതശാസ്ത്ര ആശയങ്ങളെക്കുറിച്ചുള്ള പഠനമാണ് ശുദ്ധമായ ഗണിതശാസ്ത്രം. ഈ ആശയങ്ങൾ യഥാർത്ഥ ലോകത്തിലെ ആശങ്കകളിൽ നിന്ന് ഉത്ഭവിച്ചേക്കാം, ലഭിച്ച ഫലങ്ങൾ പിന്നീട് പ്രായോഗിക പ്രയോഗങ്ങൾക്ക് ഉപയോഗപ്രദമാകും, പക്ഷേ ശുദ്ധമായ ഗണിതശാസ്ത്രജ്ഞർ പ്രാഥമികമായി അത്തരം ആപ്ലിക്കേഷനുകളാൽ പ്രചോദിതരല്ല. പകരം, അടിസ്ഥാന തത്വങ്ങളുടെ യുക്തിസഹമായ പ്രത്യാഘാതങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള ബൗദ്ധിക വെല്ലുവിളിയും സൗന്ദര്യാത്മക സൗന്ദര്യവുമാണ് അപ്പീലിന് കാരണം.
ഗണിത വസ്‌തു: ഗണിതശാസ്ത്രത്തിൽ ഉടലെടുക്കുന്ന ഒരു അമൂർത്തമായ ആശയമാണ് ഗണിതശാസ്ത്ര ഒബ്ജക്റ്റ് . ഗണിതശാസ്ത്രത്തിന്റെ സാധാരണ ഭാഷയിൽ, ഒബ്ജക്റ്റ് formal ദ്യോഗികമായി നിർവചിക്കപ്പെട്ടിട്ടുള്ള ഒന്നാണ്, കൂടാതെ ഒരാൾക്ക് കിഴിവുള്ള യുക്തിയും ഗണിതശാസ്ത്ര തെളിവുകളും ചെയ്യാം. സാധാരണഗതിയിൽ, ഒരു ഗണിത വസ്‌തു ഒരു വേരിയബിളിന് നിർണ്ണയിക്കാവുന്ന ഒരു മൂല്യമാകാം, അതിനാൽ സൂത്രവാക്യങ്ങളിൽ ഉൾപ്പെടാം. സാധാരണയായി കണ്ടുമുട്ടുന്ന ഗണിത വസ്‌തുക്കളിൽ അക്കങ്ങൾ, സെറ്റുകൾ, പ്രവർത്തനങ്ങൾ, പദപ്രയോഗങ്ങൾ, ജ്യാമിതീയ രൂപങ്ങൾ, മറ്റ് ഗണിത വസ്തുക്കളുടെ രൂപാന്തരങ്ങൾ, ഇടങ്ങൾ എന്നിവ ഉൾപ്പെടുന്നു. ഗണിത വസ്‌തുക്കൾ വളരെ സങ്കീർണ്ണമായിരിക്കും; ഉദാഹരണത്തിന്, പ്രമേയം, തെളിവുകൾ, സിദ്ധാന്തങ്ങൾ എന്നിവ പോലും പ്രൂഫ് സിദ്ധാന്തത്തിലെ ഗണിത വസ്‌തുക്കളായി കണക്കാക്കപ്പെടുന്നു.
ഗണിത പ്രശ്‌നം: ഗണിതശാസ്ത്ര രീതികളുപയോഗിച്ച് പ്രതിനിധീകരിക്കാനും വിശകലനം ചെയ്യാനും പരിഹരിക്കാനും സാധ്യതയുള്ള ഒരു പ്രശ്നമാണ് ഗണിതശാസ്ത്ര പ്രശ്നം . സൗരയൂഥത്തിലെ ഗ്രഹങ്ങളുടെ ഭ്രമണപഥം കണക്കുകൂട്ടുക, അല്ലെങ്കിൽ ഹിൽബെർട്ടിന്റെ പ്രശ്നങ്ങൾ പോലുള്ള കൂടുതൽ അമൂർത്ത സ്വഭാവത്തിന്റെ പ്രശ്നം പോലുള്ള ഒരു യഥാർത്ഥ ലോക പ്രശ്‌നമാണിത്. റസ്സലിന്റെ വിരോധാഭാസം പോലുള്ള ഗണിതശാസ്ത്രത്തിന്റെ സ്വഭാവത്തെ സൂചിപ്പിക്കുന്ന ഒരു പ്രശ്നവുമാണിത്.
ശുദ്ധമായ ഗണിതശാസ്ത്രം: ഗണിതശാസ്ത്രത്തിന് പുറത്തുള്ള ഏതൊരു ആപ്ലിക്കേഷനിൽ നിന്നും സ്വതന്ത്രമായി ഗണിതശാസ്ത്ര ആശയങ്ങളെക്കുറിച്ചുള്ള പഠനമാണ് ശുദ്ധമായ ഗണിതശാസ്ത്രം. ഈ ആശയങ്ങൾ യഥാർത്ഥ ലോകത്തിലെ ആശങ്കകളിൽ നിന്ന് ഉത്ഭവിച്ചേക്കാം, ലഭിച്ച ഫലങ്ങൾ പിന്നീട് പ്രായോഗിക പ്രയോഗങ്ങൾക്ക് ഉപയോഗപ്രദമാകും, പക്ഷേ ശുദ്ധമായ ഗണിതശാസ്ത്രജ്ഞർ പ്രാഥമികമായി അത്തരം ആപ്ലിക്കേഷനുകളാൽ പ്രചോദിതരല്ല. പകരം, അടിസ്ഥാന തത്വങ്ങളുടെ യുക്തിസഹമായ പ്രത്യാഘാതങ്ങൾ പരിഹരിക്കുന്നതിനുള്ള ബൗദ്ധിക വെല്ലുവിളിയും സൗന്ദര്യാത്മക സൗന്ദര്യവുമാണ് അപ്പീലിന് കാരണം.
രീതി (കമ്പ്യൂട്ടർ പ്രോഗ്രാമിംഗ്): ഒബ്ജക്റ്റ് ഓറിയന്റഡ് പ്രോഗ്രാമിംഗിലെ ഒരു രീതി (ഒഒപി) ഒരു സന്ദേശവും ഒബ്ജക്റ്റുമായി ബന്ധപ്പെട്ട ഒരു പ്രക്രിയയാണ്. ഒരു വസ്തുവിൽ ഡാറ്റയും പെരുമാറ്റവും അടങ്ങിയിരിക്കുന്നു; ഇവ ഒരു ഇന്റർഫേസ് ഉൾക്കൊള്ളുന്നു, അത് അതിന്റെ വിവിധ ഉപഭോക്താക്കളിൽ ഏതെങ്കിലും ഒബ്ജക്റ്റ് എങ്ങനെ ഉപയോഗിക്കാമെന്ന് വ്യക്തമാക്കുന്നു.
ആശയപരമായ മാതൃക: മോഡൽ പ്രതിനിധീകരിക്കുന്ന ഒരു വിഷയം അറിയാനോ മനസിലാക്കാനോ അനുകരിക്കാനോ ആളുകളെ സഹായിക്കുന്നതിന് ഉപയോഗിക്കുന്ന ആശയങ്ങളുടെ ഘടനയിൽ നിർമ്മിച്ച ഒരു സിസ്റ്റത്തിന്റെ പ്രാതിനിധ്യമാണ് ഒരു ആശയപരമായ മാതൃക . ഇത് ഒരു കൂട്ടം സങ്കൽപ്പങ്ങൾ കൂടിയാണ്. വിപരീതമായി, ഭ physical തിക മാതൃകകൾ ഭ physical തിക വസ്തുക്കളാണ്; ഉദാഹരണത്തിന്, ഒരു കളിപ്പാട്ട മോഡൽ ഒത്തുചേരുകയും അത് പ്രതിനിധീകരിക്കുന്ന ഒബ്ജക്റ്റ് പോലെ പ്രവർത്തിക്കുകയും ചെയ്യാം.
അമൂർത്ത മോഡൽ സിദ്ധാന്തം: ഗണിതശാസ്ത്ര യുക്തിയിൽ, ഫസ്റ്റ് ഓർഡർ ലോജിക്കിന്റെയും അവയുടെ മോഡലുകളുടെയും വിപുലീകരണങ്ങളുടെ പൊതുവായ സവിശേഷതകൾ പഠിക്കുന്ന മോഡൽ സിദ്ധാന്തത്തിന്റെ പൊതുവൽക്കരണമാണ് അമൂർത്ത മോഡൽ സിദ്ധാന്തം .
സമ്പൂർണ്ണ സംഗീതം: ഒന്നിനെക്കുറിച്ചും വ്യക്തമായി "പറയാത്ത" സംഗീതമാണ് സമ്പൂർണ്ണ സംഗീതം ; പ്രോഗ്രാം സംഗീതത്തിന് വിപരീതമായി, അത് പ്രാതിനിധ്യമില്ലാത്തതാണ്. 18-ആം നൂറ്റാണ്ടിന്റെ അവസാനത്തിൽ ജർമ്മൻ റൊമാന്റിസിസത്തിന്റെ രചയിതാക്കളായ വിൽഹെം ഹെൻ‌റിക് വാക്കൻ‌റോഡർ, ലുഡ്‌വിഗ് ടിക്, ഇടി‌എ ഹോഫ്മാൻ എന്നിവരുടെ രചനകളിൽ കേവല സംഗീതത്തെക്കുറിച്ചുള്ള ആശയം വികസിപ്പിച്ചെങ്കിലും 1846 വരെ ഈ പദം ഉപയോഗിച്ചിരുന്നില്ല, അവിടെ ആദ്യമായി റിച്ചാർഡ് വാഗ്നർ ഉപയോഗിച്ചു ബീറ്റോവന്റെ ഒമ്പതാമത്തെ സിംഫണിയിലേക്കുള്ള ഒരു പ്രോഗ്രാമിൽ.
അമൂർത്ത അസംബന്ധം: ഗണിതശാസ്ത്രത്തിൽ, അമൂർത്ത അസംബന്ധം , പൊതുവായ അമൂർത്ത അസംബന്ധം , സാമാന്യവൽക്കരിച്ച അമൂർത്ത അസംബന്ധം , പൊതുവായ അസംബന്ധം എന്നിവ ഗണിതശാസ്ത്രജ്ഞർ വിഭാഗ സിദ്ധാന്തവും ഹോമോളജിക്കൽ ആൾജിബ്രയുമായി ബന്ധപ്പെട്ട അമൂർത്ത രീതികളെ വിവരിക്കാൻ ഉപയോഗിക്കുന്ന പദങ്ങളാണ്. കൂടുതൽ സാധാരണമായി, "അമൂർത്ത അസംബന്ധം" എന്നത് കാറ്റഗറി-സൈദ്ധാന്തിക രീതികളെ ആശ്രയിക്കുന്ന ഒരു തെളിവിനെ സൂചിപ്പിക്കാം, അല്ലെങ്കിൽ കാറ്റഗറി തിയറിയുടെ പഠനത്തെപ്പോലും.
നാമം: ഒരു നാമം പോലുള്ള ജീവികൾ, സ്ഥലങ്ങൾ, പ്രവർത്തനങ്ങൾ, ഗുണങ്ങൾ നിലനില്പിന്റെ സംസ്ഥാനങ്ങളിൽ, അല്ലെങ്കിൽ ആശയങ്ങൾ ഒരു പ്രത്യേക വസ്തു വസ്തുക്കളോ സെറ്റ് പേരായി പ്രവർത്തനങ്ങൾ ഒരു വാക്കാണ്. എന്നിരുന്നാലും, നാമജപം ഒരു സെമാന്റിക് വിഭാഗമല്ല, അതിനാൽ അതിന്റെ അർത്ഥത്തിന്റെ അടിസ്ഥാനത്തിൽ അതിനെ നിർവചിക്കാൻ കഴിയില്ല. അങ്ങനെ, ക്രിയകളും അസ്തിത്വത്തിന്റെ അവസ്ഥകളും ക്രിയകൾ, ഗുണവിശേഷങ്ങൾ നാമവിശേഷണങ്ങൾ, സ്ഥലങ്ങൾ ക്രിയകൾ എന്നിവയാൽ പ്രകടിപ്പിക്കാം. ഭാഷാപരമായി, ഒരു നാമം ഒരു വലിയ, തുറന്ന സംഭാഷണത്തിലെ അംഗമാണ്, അതിന്റെ അംഗങ്ങൾക്ക് ഒരു ഉപവാക്യം, ക്രിയയുടെ ഒബ്ജക്റ്റ് അല്ലെങ്കിൽ ഒരു പ്രീപോസിഷന്റെ ഒബ്ജക്റ്റ് എന്നിവയിലെ പ്രധാന പദമായി സംഭവിക്കാം.
കോൺക്രീറ്റ് നമ്പർ: ഒരൊറ്റ എന്റിറ്റിയായി ഒരു സംഖ്യയായ ഒരു അമൂർത്ത സംഖ്യ അല്ലെങ്കിൽ സംഖ്യാ സംഖ്യകൾക്ക് വിപരീതമായി, കണക്കാക്കപ്പെടുന്ന കാര്യങ്ങളുമായി ബന്ധപ്പെട്ട ഒരു സംഖ്യയാണ് കോൺക്രീറ്റ് സംഖ്യ അല്ലെങ്കിൽ സംഖ്യാ സംഖ്യ. ഉദാഹരണത്തിന്, "അഞ്ച് ആപ്പിൾ", "പൈയുടെ പകുതി" എന്നിവ കോൺക്രീറ്റ് നമ്പറുകളാണ്, അതേസമയം "അഞ്ച്", "ഒരു പകുതി" എന്നിവ അമൂർത്ത സംഖ്യകളാണ്. ഗണിതശാസ്ത്രത്തിൽ "സംഖ്യ" എന്ന പദം സാധാരണയായി ഒരു അമൂർത്ത സംഖ്യയെ അർത്ഥമാക്കുന്നു. ഒരു യൂണിറ്റ് അളവിലുള്ള കോൺക്രീറ്റ് നമ്പറാണ് ഒരു ഡിനോമിനേറ്റ് നമ്പർ . ഉദാഹരണത്തിന്, "5 ഇഞ്ച്" എന്നത് ഒരു ഡിനോമിനേറ്റ് നമ്പറാണ്, കാരണം അതിന് ശേഷം യൂണിറ്റ് ഇഞ്ച് ഉണ്ട്.
കോൺക്രീറ്റ് നമ്പർ: ഒരൊറ്റ എന്റിറ്റിയായി ഒരു സംഖ്യയായ ഒരു അമൂർത്ത സംഖ്യ അല്ലെങ്കിൽ സംഖ്യാ സംഖ്യകൾക്ക് വിപരീതമായി, കണക്കാക്കപ്പെടുന്ന കാര്യങ്ങളുമായി ബന്ധപ്പെട്ട ഒരു സംഖ്യയാണ് കോൺക്രീറ്റ് സംഖ്യ അല്ലെങ്കിൽ സംഖ്യാ സംഖ്യ. ഉദാഹരണത്തിന്, "അഞ്ച് ആപ്പിൾ", "പൈയുടെ പകുതി" എന്നിവ കോൺക്രീറ്റ് നമ്പറുകളാണ്, അതേസമയം "അഞ്ച്", "ഒരു പകുതി" എന്നിവ അമൂർത്ത സംഖ്യകളാണ്. ഗണിതശാസ്ത്രത്തിൽ "സംഖ്യ" എന്ന പദം സാധാരണയായി ഒരു അമൂർത്ത സംഖ്യയെ അർത്ഥമാക്കുന്നു. ഒരു യൂണിറ്റ് അളവിലുള്ള കോൺക്രീറ്റ് നമ്പറാണ് ഒരു ഡിനോമിനേറ്റ് നമ്പർ . ഉദാഹരണത്തിന്, "5 ഇഞ്ച്" എന്നത് ഒരു ഡിനോമിനേറ്റ് നമ്പറാണ്, കാരണം അതിന് ശേഷം യൂണിറ്റ് ഇഞ്ച് ഉണ്ട്.
അമൂർത്തവും കോൺക്രീറ്റും: മെറ്റാഫിസിക്‌സിൽ, അമൂർത്തവും കോൺക്രീറ്റും തമ്മിലുള്ള വ്യത്യാസം രണ്ട് തരം എന്റിറ്റികൾ തമ്മിലുള്ള വിഭജനത്തെ സൂചിപ്പിക്കുന്നു. ഈ വ്യത്യാസത്തിന് അടിസ്ഥാന മെറ്റാഫിസിക്കൽ പ്രാധാന്യമുണ്ടെന്ന് പല തത്ത്വചിന്തകരും അഭിപ്രായപ്പെടുന്നു. കോൺക്രീറ്റ് വസ്തുക്കളുടെ ഉദാഹരണങ്ങളിൽ സസ്യങ്ങൾ, മനുഷ്യർ, ഗ്രഹങ്ങൾ എന്നിവ ഉൾപ്പെടുന്നു, അതേസമയം സംഖ്യകൾ, സെറ്റുകൾ, നിർദ്ദേശങ്ങൾ എന്നിവ അമൂർത്ത വസ്തുക്കളാണ് . ദൃ ret തയുടെയും അമൂർത്തതയുടെയും സ്വഭാവ ചിഹ്നങ്ങൾ എന്താണെന്നതിന് പൊതുവായ അഭിപ്രായ സമന്വയമില്ല. (1) സ്ഥല-സമയത്തിനകത്തോ പുറത്തോ ഉള്ള അസ്തിത്വം, (2) കാരണങ്ങളും ഫലങ്ങളും ഉണ്ടോ ഇല്ലയോ, (3) അനിശ്ചിതത്വത്തിലോ ആവശ്യമുള്ളതോ ഉള്ള അസ്തിത്വം, (4) പ്രത്യേകമോ സാർവത്രികമോ (5) ശാരീരികമോ മാനസികമോ ആയ മേഖലയിലോ അല്ലാതെയോ. ഈ വൈവിധ്യമാർന്ന കാഴ്ചപ്പാടുകൾ ഉണ്ടായിരുന്നിട്ടും, മിക്ക വസ്തുക്കളും അമൂർത്തമോ കോൺക്രീറ്റോ ആണോ എന്നതിനെക്കുറിച്ച് വിശാലമായ ധാരണയുണ്ട്. അതിനാൽ മിക്ക വ്യാഖ്യാനങ്ങളിലും, ഈ കാഴ്ചപ്പാടുകളെല്ലാം സമ്മതിക്കും, ഉദാഹരണത്തിന്, സസ്യങ്ങൾ കോൺക്രീറ്റ് വസ്തുക്കളാണ്, അക്കങ്ങൾ അമൂർത്ത വസ്തുക്കളാണ്.
അമൂർത്തമായ ഒബ്ജക്റ്റ് സിദ്ധാന്തം: അമൂർത്ത വസ്തുക്കളെ സംബന്ധിച്ച മെറ്റാഫിസിക്‌സിന്റെ ഒരു ശാഖയാണ് അബ്‌സ്ട്രാക്റ്റ് ഒബ്ജക്റ്റ് തിയറി ( AOT ). 1981 ൽ മെറ്റാഫിഷ്യൻ എഡ്വേർഡ് സാൽറ്റ ആവിഷ്കരിച്ച ഈ സിദ്ധാന്തം ഗണിതശാസ്ത്ര പ്ലാറ്റോണിസത്തിന്റെ വികാസമായിരുന്നു.
അമൂർത്തവും കോൺക്രീറ്റും: മെറ്റാഫിസിക്‌സിൽ, അമൂർത്തവും കോൺക്രീറ്റും തമ്മിലുള്ള വ്യത്യാസം രണ്ട് തരം എന്റിറ്റികൾ തമ്മിലുള്ള വിഭജനത്തെ സൂചിപ്പിക്കുന്നു. ഈ വ്യത്യാസത്തിന് അടിസ്ഥാന മെറ്റാഫിസിക്കൽ പ്രാധാന്യമുണ്ടെന്ന് പല തത്ത്വചിന്തകരും അഭിപ്രായപ്പെടുന്നു. കോൺക്രീറ്റ് വസ്തുക്കളുടെ ഉദാഹരണങ്ങളിൽ സസ്യങ്ങൾ, മനുഷ്യർ, ഗ്രഹങ്ങൾ എന്നിവ ഉൾപ്പെടുന്നു, അതേസമയം സംഖ്യകൾ, സെറ്റുകൾ, നിർദ്ദേശങ്ങൾ എന്നിവ അമൂർത്ത വസ്തുക്കളാണ് . ദൃ ret തയുടെയും അമൂർത്തതയുടെയും സ്വഭാവ ചിഹ്നങ്ങൾ എന്താണെന്നതിന് പൊതുവായ അഭിപ്രായ സമന്വയമില്ല. (1) സ്ഥല-സമയത്തിനകത്തോ പുറത്തോ ഉള്ള അസ്തിത്വം, (2) കാരണങ്ങളും ഫലങ്ങളും ഉണ്ടോ ഇല്ലയോ, (3) അനിശ്ചിതത്വത്തിലോ ആവശ്യമുള്ളതോ ഉള്ള അസ്തിത്വം, (4) പ്രത്യേകമോ സാർവത്രികമോ (5) ശാരീരികമോ മാനസികമോ ആയ മേഖലയിലോ അല്ലാതെയോ. ഈ വൈവിധ്യമാർന്ന കാഴ്ചപ്പാടുകൾ ഉണ്ടായിരുന്നിട്ടും, മിക്ക വസ്തുക്കളും അമൂർത്തമോ കോൺക്രീറ്റോ ആണോ എന്നതിനെക്കുറിച്ച് വിശാലമായ ധാരണയുണ്ട്. അതിനാൽ മിക്ക വ്യാഖ്യാനങ്ങളിലും, ഈ കാഴ്ചപ്പാടുകളെല്ലാം സമ്മതിക്കും, ഉദാഹരണത്തിന്, സസ്യങ്ങൾ കോൺക്രീറ്റ് വസ്തുക്കളാണ്, അക്കങ്ങൾ അമൂർത്ത വസ്തുക്കളാണ്.
പ്രോപ്പർട്ടി സംഗ്രഹം: ഒരു പ്രത്യേക പാർസലുമായി ബന്ധപ്പെട്ട ഇടപാടുകൾ വിവരിക്കുന്ന നിയമപരമായ രേഖകളുടെ ഒരു ശേഖരമാണ് പ്രോപ്പർട്ടി അബ്‌സ്ട്രാക്റ്റ് . ഡീഡുകൾ, മോർട്ട്ഗേജുകൾ, വിൽപത്രം, പ്രോബേറ്റ് റെക്കോർഡുകൾ, കോടതി വ്യവഹാരങ്ങൾ, നികുതി വിൽപ്പന എന്നിവയെക്കുറിച്ചുള്ള പരാമർശങ്ങൾ സാധാരണയായി ഉൾപ്പെടുത്തിയിട്ടുണ്ട് - അടിസ്ഥാനപരമായി, സ്വത്തെ ബാധിക്കുന്ന ഏതെങ്കിലും നിയമ പ്രമാണം.
ന്യായവിധിയുടെ സംഗ്രഹം: " വിധിന്യായത്തിന്റെ സംഗ്രഹം" എന്നത് ഒരു വിധിന്യായത്തിന്റെ രേഖാമൂലമുള്ള സംഗ്രഹമാണ്, അത് നഷ്ടപ്പെട്ട പ്രതി വ്യവഹാരത്തിൽ വിജയിച്ച വ്യക്തിക്ക് എത്ര പണം നൽകണം, വിധിന്യായത്തിൽ നൽകേണ്ട പലിശ നിരക്ക്, കോടതി ചെലവുകൾ, ഏതെങ്കിലും നിർദ്ദിഷ്ട ഉത്തരവുകൾ നഷ്ടപ്പെട്ട പ്രതി അനുസരിക്കണം, ഏത് അമൂർത്തത്തെ അംഗീകരിക്കുകയും സ്റ്റാമ്പ് ചെയ്യുകയും ചെയ്യുന്നു, അതുവഴി ഇത് റെക്കോർഡുചെയ്യാനും സർക്കാരുമായി official ദ്യോഗികമാക്കാനും കഴിയും. വിധിന്യായത്തിന്റെ സംഗ്രഹം, ഒരു പൊതു റെക്കോർഡ് സൃഷ്ടിക്കുകയും ആവശ്യമെങ്കിൽ ഒരു അവകാശം അല്ലെങ്കിൽ ക്ലെയിം സൃഷ്ടിക്കുകയും ചെയ്യുക. വിധിന്യായത്തിന്റെ സംഗ്രഹം രേഖപ്പെടുത്തിയിരിക്കുന്ന രാജ്യത്ത് സ്ഥിതിചെയ്യുന്ന പ്രതിയുടെ ഉടമസ്ഥതയിലുള്ളതോ പിന്നീട് നേടിയതോ ആയ ഏതെങ്കിലും റിയൽ എസ്റ്റേറ്റ് സ്വത്തിൽ. പരാജിതൻ വിധി സ്വമേധയാ നൽകുന്നില്ലെങ്കിൽ, വിജയിക്ക് ഒരു ഷെരീഫിന്റെ ഏതെങ്കിലും സ്വത്ത് വിൽക്കാൻ നിർബന്ധിക്കാൻ കഴിയും. നിരവധി പ്രശ്‌നങ്ങളുണ്ട്: 1) പരാജിതന് റിയൽ എസ്റ്റേറ്റ് സ്വത്ത് ഉള്ള രാജ്യം കണ്ടെത്തുന്നതിന്; 2) ന്യായവിധി അവകാശത്തിന് മുമ്പായി സുരക്ഷിതമായ വായ്പകൾ, നികുതി അവകാശികൾ കൂടാതെ / അല്ലെങ്കിൽ മറ്റ് വിധിന്യായങ്ങൾ എന്നിവ ഉണ്ടാകാനുള്ള സാധ്യത; 3) പരാജിതൻ / കടക്കാരൻ പാപ്പരാകാനും കടം വീട്ടുന്നത് ഒഴിവാക്കാനുമുള്ള സാധ്യത.
പ്രോപ്പർട്ടി സംഗ്രഹം: ഒരു പ്രത്യേക പാർസലുമായി ബന്ധപ്പെട്ട ഇടപാടുകൾ വിവരിക്കുന്ന നിയമപരമായ രേഖകളുടെ ഒരു ശേഖരമാണ് പ്രോപ്പർട്ടി അബ്‌സ്ട്രാക്റ്റ് . ഡീഡുകൾ, മോർട്ട്ഗേജുകൾ, വിൽപത്രം, പ്രോബേറ്റ് റെക്കോർഡുകൾ, കോടതി വ്യവഹാരങ്ങൾ, നികുതി വിൽപ്പന എന്നിവയെക്കുറിച്ചുള്ള പരാമർശങ്ങൾ സാധാരണയായി ഉൾപ്പെടുത്തിയിട്ടുണ്ട് - അടിസ്ഥാനപരമായി, സ്വത്തെ ബാധിക്കുന്ന ഏതെങ്കിലും നിയമ പ്രമാണം.
പ്രോപ്പർട്ടി സംഗ്രഹം: ഒരു പ്രത്യേക പാർസലുമായി ബന്ധപ്പെട്ട ഇടപാടുകൾ വിവരിക്കുന്ന നിയമപരമായ രേഖകളുടെ ഒരു ശേഖരമാണ് പ്രോപ്പർട്ടി അബ്‌സ്ട്രാക്റ്റ് . ഡീഡുകൾ, മോർട്ട്ഗേജുകൾ, വിൽപത്രം, പ്രോബേറ്റ് റെക്കോർഡുകൾ, കോടതി വ്യവഹാരങ്ങൾ, നികുതി വിൽപ്പന എന്നിവയെക്കുറിച്ചുള്ള പരാമർശങ്ങൾ സാധാരണയായി ഉൾപ്പെടുത്തിയിട്ടുണ്ട് - അടിസ്ഥാനപരമായി, സ്വത്തെ ബാധിക്കുന്ന ഏതെങ്കിലും നിയമ പ്രമാണം.
കാസിനിയ (ജേണൽ): ചഷിനിഅ ഡെലവെയർ വാലി പക്ഷിശാസ്ത്ര ക്ലബ് (ദ്വൊച്) എന്ന ജേണൽ ആണ്. കിഴക്കൻ പെൻ‌സിൽ‌വാനിയ, ന്യൂജേഴ്‌സി, ഡെലവെയർ എന്നിവയുടെ പക്ഷിശാസ്ത്രവുമായി ബന്ധപ്പെട്ട പ്രബന്ധങ്ങൾ ഉൾക്കൊള്ളുന്നതാണ് ജേണൽ. എഴുപത്തിമൂന്ന് ലക്കങ്ങൾ ഇന്നുവരെ പ്രസിദ്ധീകരിച്ചു. അഞ്ച് പ്രാരംഭ വാല്യങ്ങൾ (1890–1900) ഡെലവെയർ വാലി ഓർണിത്തോളജിക്കൽ ക്ലബിന്റെ സംക്ഷിപ്തം എന്ന പേരിൽ പ്രസിദ്ധീകരിച്ചു, തുടർന്ന് 1901 ൽ പക്ഷിശാസ്ത്രജ്ഞനായ ജോൺ കാസിന്റെ ബഹുമാനാർത്ഥം ജേണൽ പുനർനാമകരണം ചെയ്യപ്പെട്ടു.
സംഗ്രഹം (നിയമം): നിയമത്തിൽ, ഒരു നീണ്ട നിയമ പ്രമാണത്തിന്റെ അല്ലെങ്കിൽ ബന്ധപ്പെട്ട നിരവധി നിയമ പ്രബന്ധങ്ങളുടെ ഏറ്റവും പ്രധാനപ്പെട്ട പോയിന്റുകൾ ഉൾക്കൊള്ളുന്ന ഒരു ഹ്രസ്വ പ്രസ്താവനയാണ് അമൂർത്തമായത് .
പ്രോപ്പർട്ടി സംഗ്രഹം: ഒരു പ്രത്യേക പാർസലുമായി ബന്ധപ്പെട്ട ഇടപാടുകൾ വിവരിക്കുന്ന നിയമപരമായ രേഖകളുടെ ഒരു ശേഖരമാണ് പ്രോപ്പർട്ടി അബ്‌സ്ട്രാക്റ്റ് . ഡീഡുകൾ, മോർട്ട്ഗേജുകൾ, വിൽപത്രം, പ്രോബേറ്റ് റെക്കോർഡുകൾ, കോടതി വ്യവഹാരങ്ങൾ, നികുതി വിൽപ്പന എന്നിവയെക്കുറിച്ചുള്ള പരാമർശങ്ങൾ സാധാരണയായി ഉൾപ്പെടുത്തിയിട്ടുണ്ട് - അടിസ്ഥാനപരമായി, സ്വത്തെ ബാധിക്കുന്ന ഏതെങ്കിലും നിയമ പ്രമാണം.
അമൂർത്ത കല: ലോകത്തിലെ വിഷ്വൽ റഫറൻസുകളിൽ നിന്ന് ഒരു പരിധിവരെ സ്വാതന്ത്ര്യത്തോടുകൂടിയ ഒരു രചന സൃഷ്ടിക്കാൻ അമൂർത്ത കല രൂപം, രൂപം, നിറം, രേഖ എന്നിവയുടെ വിഷ്വൽ ഭാഷ ഉപയോഗിക്കുന്നു. പാശ്ചാത്യ കല, നവോത്ഥാനം മുതൽ പത്തൊൻപതാം നൂറ്റാണ്ടിന്റെ മദ്ധ്യകാലം വരെ, കാഴ്ചപ്പാടിന്റെ യുക്തിയും ദൃശ്യമായ യാഥാർത്ഥ്യത്തിന്റെ ഒരു മിഥ്യാധാരണയെ പുനർനിർമ്മിക്കാനുള്ള ശ്രമവുമാണ്. പത്തൊൻപതാം നൂറ്റാണ്ടിന്റെ അവസാനത്തോടെ സാങ്കേതികവിദ്യ, ശാസ്ത്രം, തത്ത്വചിന്ത എന്നിവയിൽ സംഭവിക്കുന്ന അടിസ്ഥാനപരമായ മാറ്റങ്ങൾ ഉൾക്കൊള്ളുന്ന ഒരു പുതിയ തരം കല സൃഷ്ടിക്കേണ്ടതുണ്ടെന്ന് പല കലാകാരന്മാർക്കും തോന്നി. വ്യക്തിഗത കലാകാരന്മാർ അവരുടെ സൈദ്ധാന്തിക വാദങ്ങൾ ഉന്നയിച്ച ഉറവിടങ്ങൾ വൈവിധ്യപൂർണ്ണമായിരുന്നു, അക്കാലത്ത് പാശ്ചാത്യ സംസ്കാരത്തിന്റെ എല്ലാ മേഖലകളിലെയും സാമൂഹികവും ബ ual ദ്ധികവുമായ മുൻ‌തൂക്കങ്ങൾ പ്രതിഫലിപ്പിച്ചു.
അമൂർത്ത കല: ലോകത്തിലെ വിഷ്വൽ റഫറൻസുകളിൽ നിന്ന് ഒരു പരിധിവരെ സ്വാതന്ത്ര്യത്തോടുകൂടിയ ഒരു രചന സൃഷ്ടിക്കാൻ അമൂർത്ത കല രൂപം, രൂപം, നിറം, രേഖ എന്നിവയുടെ വിഷ്വൽ ഭാഷ ഉപയോഗിക്കുന്നു. പാശ്ചാത്യ കല, നവോത്ഥാനം മുതൽ പത്തൊൻപതാം നൂറ്റാണ്ടിന്റെ മദ്ധ്യകാലം വരെ, കാഴ്ചപ്പാടിന്റെ യുക്തിയും ദൃശ്യമായ യാഥാർത്ഥ്യത്തിന്റെ ഒരു മിഥ്യാധാരണയെ പുനർനിർമ്മിക്കാനുള്ള ശ്രമവുമാണ്. പത്തൊൻപതാം നൂറ്റാണ്ടിന്റെ അവസാനത്തോടെ സാങ്കേതികവിദ്യ, ശാസ്ത്രം, തത്ത്വചിന്ത എന്നിവയിൽ സംഭവിക്കുന്ന അടിസ്ഥാനപരമായ മാറ്റങ്ങൾ ഉൾക്കൊള്ളുന്ന ഒരു പുതിയ തരം കല സൃഷ്ടിക്കേണ്ടതുണ്ടെന്ന് പല കലാകാരന്മാർക്കും തോന്നി. വ്യക്തിഗത കലാകാരന്മാർ അവരുടെ സൈദ്ധാന്തിക വാദങ്ങൾ ഉന്നയിച്ച ഉറവിടങ്ങൾ വൈവിധ്യപൂർണ്ണമായിരുന്നു, അക്കാലത്ത് പാശ്ചാത്യ സംസ്കാരത്തിന്റെ എല്ലാ മേഖലകളിലെയും സാമൂഹികവും ബ ual ദ്ധികവുമായ മുൻ‌തൂക്കങ്ങൾ പ്രതിഫലിപ്പിച്ചു.
അമൂർത്ത പെയിന്റിംഗ് (പാസ്മോർ): അമൂർത്തമായ പെയിന്റിംഗ് വിക്ടർ പസ്മൊരെ ഒരു 1998 അമൂർത്ത എണ്ണച്ചായം ആണ്.
അമൂർത്ത കല: ലോകത്തിലെ വിഷ്വൽ റഫറൻസുകളിൽ നിന്ന് ഒരു പരിധിവരെ സ്വാതന്ത്ര്യത്തോടുകൂടിയ ഒരു രചന സൃഷ്ടിക്കാൻ അമൂർത്ത കല രൂപം, രൂപം, നിറം, രേഖ എന്നിവയുടെ വിഷ്വൽ ഭാഷ ഉപയോഗിക്കുന്നു. പാശ്ചാത്യ കല, നവോത്ഥാനം മുതൽ പത്തൊൻപതാം നൂറ്റാണ്ടിന്റെ മദ്ധ്യകാലം വരെ, കാഴ്ചപ്പാടിന്റെ യുക്തിയും ദൃശ്യമായ യാഥാർത്ഥ്യത്തിന്റെ ഒരു മിഥ്യാധാരണയെ പുനർനിർമ്മിക്കാനുള്ള ശ്രമവുമാണ്. പത്തൊൻപതാം നൂറ്റാണ്ടിന്റെ അവസാനത്തോടെ സാങ്കേതികവിദ്യ, ശാസ്ത്രം, തത്ത്വചിന്ത എന്നിവയിൽ സംഭവിക്കുന്ന അടിസ്ഥാനപരമായ മാറ്റങ്ങൾ ഉൾക്കൊള്ളുന്ന ഒരു പുതിയ തരം കല സൃഷ്ടിക്കേണ്ടതുണ്ടെന്ന് പല കലാകാരന്മാർക്കും തോന്നി. വ്യക്തിഗത കലാകാരന്മാർ അവരുടെ സൈദ്ധാന്തിക വാദങ്ങൾ ഉന്നയിച്ച ഉറവിടങ്ങൾ വൈവിധ്യപൂർണ്ണമായിരുന്നു, അക്കാലത്ത് പാശ്ചാത്യ സംസ്കാരത്തിന്റെ എല്ലാ മേഖലകളിലെയും സാമൂഹികവും ബ ual ദ്ധികവുമായ മുൻ‌തൂക്കങ്ങൾ പ്രതിഫലിപ്പിച്ചു.
സംഗ്രഹ വിശദാംശങ്ങൾ: അമൂർത്തമായ വിശദാംശങ്ങളും സംക്ഷിപ്ത വസ്തുക്കളും മെറ്റാഫിസിക്കൽ എന്റിറ്റികളാണ്.
സംഗ്രഹ വിശദാംശങ്ങൾ: അമൂർത്തമായ വിശദാംശങ്ങളും സംക്ഷിപ്ത വസ്തുക്കളും മെറ്റാഫിസിക്കൽ എന്റിറ്റികളാണ്.
സംഗ്രഹ വിശദാംശങ്ങൾ: അമൂർത്തമായ വിശദാംശങ്ങളും സംക്ഷിപ്ത വസ്തുക്കളും മെറ്റാഫിസിക്കൽ എന്റിറ്റികളാണ്.
അമൂർത്ത ഫോട്ടോഗ്രഫി: ഒബ്ജക്റ്റ് ലോകവുമായി ഉടനടി ബന്ധമില്ലാത്തതും ഫോട്ടോഗ്രാഫിക് ഉപകരണങ്ങൾ, പ്രക്രിയകൾ അല്ലെങ്കിൽ മെറ്റീരിയലുകൾ എന്നിവ ഉപയോഗിച്ച് സൃഷ്ടിക്കപ്പെട്ടതുമായ ഒരു വിഷ്വൽ ഇമേജ് ചിത്രീകരിക്കുന്നതിനുള്ള ഒരു മാർഗമാണ് അമൂർത്ത ഫോട്ടോഗ്രഫി , ചിലപ്പോൾ നോൺ-ഒബ്ജക്റ്റ്, പരീക്ഷണാത്മക അല്ലെങ്കിൽ ആശയപരമായ ഫോട്ടോഗ്രാഫി. ഒരു അമൂർത്ത ഫോട്ടോഗ്രാഫ് കാഴ്ചക്കാരനിൽ നിന്ന് സ്വാഭാവിക രംഗത്തിന്റെ ഒരു ഭാഗം വേർതിരിച്ചെടുക്കുന്നതിന്, യഥാർത്ഥ വസ്തുക്കളിൽ നിന്ന് യാഥാർത്ഥ്യമല്ലാത്തതായി തോന്നുന്നത് സൃഷ്ടിക്കാൻ മന os പൂർവ്വം അരങ്ങേറാം, അല്ലെങ്കിൽ അതിൽ നിറം, വെളിച്ചം, നിഴൽ, ടെക്സ്ചർ, ആകാരം കൂടാതെ / അല്ലെങ്കിൽ ഒരു വികാരം, സംവേദനം അല്ലെങ്കിൽ മതിപ്പ് അറിയിക്കുന്നതിനുള്ള രൂപം. ക്യാമറ, ഡാർക്ക്‌റൂം അല്ലെങ്കിൽ കമ്പ്യൂട്ടർ പോലുള്ള പരമ്പരാഗത ഫോട്ടോഗ്രാഫിക് ഉപകരണങ്ങൾ ഉപയോഗിച്ച് ചിത്രം നിർമ്മിക്കാം, അല്ലെങ്കിൽ ഡിജിറ്റൽ അവതരണങ്ങൾ ഉൾപ്പെടെ ഫിലിം, പേപ്പർ അല്ലെങ്കിൽ മറ്റ് ഫോട്ടോഗ്രാഫിക് മീഡിയകൾ നേരിട്ട് കൈകാര്യം ചെയ്യുന്നതിലൂടെ ക്യാമറ ഉപയോഗിക്കാതെ ഇത് സൃഷ്ടിച്ചേക്കാം.
അമൂർത്ത ഫോട്ടോഗ്രഫി: ഒബ്ജക്റ്റ് ലോകവുമായി ഉടനടി ബന്ധമില്ലാത്തതും ഫോട്ടോഗ്രാഫിക് ഉപകരണങ്ങൾ, പ്രക്രിയകൾ അല്ലെങ്കിൽ മെറ്റീരിയലുകൾ എന്നിവ ഉപയോഗിച്ച് സൃഷ്ടിക്കപ്പെട്ടതുമായ ഒരു വിഷ്വൽ ഇമേജ് ചിത്രീകരിക്കുന്നതിനുള്ള ഒരു മാർഗമാണ് അമൂർത്ത ഫോട്ടോഗ്രഫി , ചിലപ്പോൾ നോൺ-ഒബ്ജക്റ്റ്, പരീക്ഷണാത്മക അല്ലെങ്കിൽ ആശയപരമായ ഫോട്ടോഗ്രാഫി. ഒരു അമൂർത്ത ഫോട്ടോഗ്രാഫ് കാഴ്ചക്കാരനിൽ നിന്ന് സ്വാഭാവിക രംഗത്തിന്റെ ഒരു ഭാഗം വേർതിരിച്ചെടുക്കുന്നതിന്, യഥാർത്ഥ വസ്തുക്കളിൽ നിന്ന് യാഥാർത്ഥ്യമല്ലാത്തതായി തോന്നുന്നത് സൃഷ്ടിക്കാൻ മന os പൂർവ്വം അരങ്ങേറാം, അല്ലെങ്കിൽ അതിൽ നിറം, വെളിച്ചം, നിഴൽ, ടെക്സ്ചർ, ആകാരം കൂടാതെ / അല്ലെങ്കിൽ ഒരു വികാരം, സംവേദനം അല്ലെങ്കിൽ മതിപ്പ് അറിയിക്കുന്നതിനുള്ള രൂപം. ക്യാമറ, ഡാർക്ക്‌റൂം അല്ലെങ്കിൽ കമ്പ്യൂട്ടർ പോലുള്ള പരമ്പരാഗത ഫോട്ടോഗ്രാഫിക് ഉപകരണങ്ങൾ ഉപയോഗിച്ച് ചിത്രം നിർമ്മിക്കാം, അല്ലെങ്കിൽ ഡിജിറ്റൽ അവതരണങ്ങൾ ഉൾപ്പെടെ ഫിലിം, പേപ്പർ അല്ലെങ്കിൽ മറ്റ് ഫോട്ടോഗ്രാഫിക് മീഡിയകൾ നേരിട്ട് കൈകാര്യം ചെയ്യുന്നതിലൂടെ ക്യാമറ ഉപയോഗിക്കാതെ ഇത് സൃഷ്ടിച്ചേക്കാം.
ഫറാസ് അൻവർ: പാകിസ്താൻ സംഗീതജ്ഞൻ, സംഗീതസംവിധായകൻ, ഗായകൻ-ഗാനരചയിതാവ്, ബാൻഡ്‌ലീഡർ, മിസ്രാബ് സ്ഥാപിച്ച ഗിറ്റാറിസ്റ്റ് എന്നിവരാണ് ഫറാസ് അൻവർ - പാക്കിസ്ഥാൻ ആസ്ഥാനമായി പ്രവർത്തിക്കുന്ന ഹെവി മെറ്റൽ സംഗീതവും ഹാർഡ് റോക്ക് വിഭാഗവും. ഇലക്ട്രിക് ഗിറ്റാറിലെ അദ്ദേഹത്തിന്റെ സംഗീത പ്രവർത്തനം രാജ്യത്തെ സംഗീത വിമർശകർ "പാകിസ്ഥാന്റെ പുരോഗമന പാറയുടെ മാസ്റ്റർ" എന്ന് വിശേഷിപ്പിച്ചിരിക്കുന്നു. അൻവർ നിലവിൽ ലയൺ മ്യൂസിക്ക് - ഫിന്നിഷ് നിർമ്മാണ, റെക്കോർഡ് ലേബൽ കമ്പനിയാണ്.
ഫറാസ് അൻവർ: പാകിസ്താൻ സംഗീതജ്ഞൻ, സംഗീതസംവിധായകൻ, ഗായകൻ-ഗാനരചയിതാവ്, ബാൻഡ്‌ലീഡർ, മിസ്രാബ് സ്ഥാപിച്ച ഗിറ്റാറിസ്റ്റ് എന്നിവരാണ് ഫറാസ് അൻവർ - പാക്കിസ്ഥാൻ ആസ്ഥാനമായി പ്രവർത്തിക്കുന്ന ഹെവി മെറ്റൽ സംഗീതവും ഹാർഡ് റോക്ക് വിഭാഗവും. ഇലക്ട്രിക് ഗിറ്റാറിലെ അദ്ദേഹത്തിന്റെ സംഗീത പ്രവർത്തനം രാജ്യത്തെ സംഗീത വിമർശകർ "പാകിസ്ഥാന്റെ പുരോഗമന പാറയുടെ മാസ്റ്റർ" എന്ന് വിശേഷിപ്പിച്ചിരിക്കുന്നു. അൻവർ നിലവിൽ ലയൺ മ്യൂസിക്ക് - ഫിന്നിഷ് നിർമ്മാണ, റെക്കോർഡ് ലേബൽ കമ്പനിയാണ്.
അമൂർത്ത പോളിറ്റോപ്പ്: ഗണിതശാസ്ത്രത്തിൽ, ഒരു ബീജഗണിതം ഭാഗികമായി ക്രമീകരിച്ച ഒരു സെറ്റ് അല്ലെങ്കിൽ പോസെറ്റാണ് അമൂർത്ത പോളിറ്റോപ്പ് , ഇത് പരമ്പരാഗത പോളിറ്റോപ്പിന്റെ കോമ്പിനേറ്റോറിയൽ ഗുണങ്ങളെ കോണുകൾ അല്ലെങ്കിൽ എഡ്ജ് ദൈർഘ്യം പോലുള്ള ജ്യാമിതീയ സവിശേഷതകൾ വ്യക്തമാക്കാതെ പിടിച്ചെടുക്കുന്നു. പോളിഗോപ്പ്, പോളിഹെഡ്ര എന്നിവയെ എത്ര അളവുകളിലേക്ക് സാമാന്യവൽക്കരിക്കുന്നു.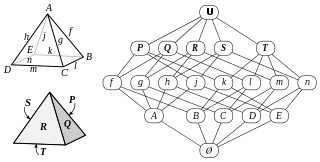
അമൂർത്ത പോളിറ്റോപ്പ്: ഗണിതശാസ്ത്രത്തിൽ, ഒരു ബീജഗണിതം ഭാഗികമായി ക്രമീകരിച്ച ഒരു സെറ്റ് അല്ലെങ്കിൽ പോസെറ്റാണ് അമൂർത്ത പോളിറ്റോപ്പ് , ഇത് പരമ്പരാഗത പോളിറ്റോപ്പിന്റെ കോമ്പിനേറ്റോറിയൽ ഗുണങ്ങളെ കോണുകൾ അല്ലെങ്കിൽ എഡ്ജ് ദൈർഘ്യം പോലുള്ള ജ്യാമിതീയ സവിശേഷതകൾ വ്യക്തമാക്കാതെ പിടിച്ചെടുക്കുന്നു. പോളിഗോപ്പ്, പോളിഹെഡ്ര എന്നിവയെ എത്ര അളവുകളിലേക്ക് സാമാന്യവൽക്കരിക്കുന്നു.
അമൂർത്ത പോളിറ്റോപ്പ്: ഗണിതശാസ്ത്രത്തിൽ, ഒരു ബീജഗണിതം ഭാഗികമായി ക്രമീകരിച്ച ഒരു സെറ്റ് അല്ലെങ്കിൽ പോസെറ്റാണ് അമൂർത്ത പോളിറ്റോപ്പ് , ഇത് പരമ്പരാഗത പോളിറ്റോപ്പിന്റെ കോമ്പിനേറ്റോറിയൽ ഗുണങ്ങളെ കോണുകൾ അല്ലെങ്കിൽ എഡ്ജ് ദൈർഘ്യം പോലുള്ള ജ്യാമിതീയ സവിശേഷതകൾ വ്യക്തമാക്കാതെ പിടിച്ചെടുക്കുന്നു. പോളിഗോപ്പ്, പോളിഹെഡ്ര എന്നിവയെ എത്ര അളവുകളിലേക്ക് സാമാന്യവൽക്കരിക്കുന്നു.
അമൂർത്ത പോളിറ്റോപ്പ്: ഗണിതശാസ്ത്രത്തിൽ, ഒരു ബീജഗണിതം ഭാഗികമായി ക്രമീകരിച്ച ഒരു സെറ്റ് അല്ലെങ്കിൽ പോസെറ്റാണ് അമൂർത്ത പോളിറ്റോപ്പ് , ഇത് പരമ്പരാഗത പോളിറ്റോപ്പിന്റെ കോമ്പിനേറ്റോറിയൽ ഗുണങ്ങളെ കോണുകൾ അല്ലെങ്കിൽ എഡ്ജ് ദൈർഘ്യം പോലുള്ള ജ്യാമിതീയ സവിശേഷതകൾ വ്യക്തമാക്കാതെ പിടിച്ചെടുക്കുന്നു. പോളിഗോപ്പ്, പോളിഹെഡ്ര എന്നിവയെ എത്ര അളവുകളിലേക്ക് സാമാന്യവൽക്കരിക്കുന്നു.
അമൂർത്ത വിശകലന സംഖ്യ സിദ്ധാന്തം: ക്ലാസിക്കൽ അനലിറ്റിക് നമ്പർ സിദ്ധാന്തത്തിന്റെ ആശയങ്ങളും സാങ്കേതികതകളും എടുത്ത് വിവിധ ഗണിതശാസ്ത്ര മേഖലകളിൽ പ്രയോഗിക്കുന്ന ഗണിതശാസ്ത്രത്തിന്റെ ഒരു ശാഖയാണ് അമൂർത്ത അനലിറ്റിക് നമ്പർ സിദ്ധാന്തം . ക്ലാസിക്കൽ പ്രൈം നമ്പർ സിദ്ധാന്തം ഒരു പ്രോട്ടോടൈപ്പിക്കൽ ഉദാഹരണമായി വർത്തിക്കുന്നു, കൂടാതെ അമൂർത്ത അസിംപ്റ്റോട്ടിക് വിതരണ ഫലങ്ങൾക്ക് is ന്നൽ നൽകുന്നു. ഇരുപതാം നൂറ്റാണ്ടിൽ ഗണിതശാസ്ത്രജ്ഞന്മാരായ ജോൺ നോപ്മാക്കർ, ആർനെ ബർലിംഗ് എന്നിവർ ഈ സിദ്ധാന്തം കണ്ടുപിടിക്കുകയും വികസിപ്പിക്കുകയും ചെയ്തു.
സംഗ്രഹം (വ്യതിചലനം): സാമാന്യവൽക്കരണം, ഗുണവിശേഷതകൾ നീക്കംചെയ്യൽ, അല്ലെങ്കിൽ വസ്തുക്കളിൽ നിന്ന് ആശയങ്ങൾ അകറ്റുക എന്നിവയുടെ ഒരു പ്രക്രിയ അല്ലെങ്കിൽ ഫലമാണ് അമൂർത്തീകരണം .
അവരുടെ യുക്തിപരമായ തീവ്രതകളിലേക്ക് എടുത്ത അമൂർത്ത തത്വങ്ങൾ: ഇംഗ്ലണ്ടിലെ ലണ്ടനിൽ നിന്നുള്ള ഡെത്ത് മെറ്റൽ ബാൻഡായ ഡാർക്ക് ഹെറസിയുടെ ഏക ആൽബമാണ് അമൂർത്ത തത്ത്വങ്ങൾ അവരുടെ യുക്തിസഹമായ തീവ്രത 1995 ൽ പുറത്തിറങ്ങിയത്.
സംഗ്രഹം: നിർദ്ദിഷ്ട ഉദാഹരണങ്ങൾ, അക്ഷര സൂചകങ്ങൾ, ആദ്യ തത്ത്വങ്ങൾ അല്ലെങ്കിൽ മറ്റ് രീതികളുടെ ഉപയോഗത്തിൽ നിന്നും വർഗ്ഗീകരണത്തിൽ നിന്നും പൊതുവായ നിയമങ്ങളും ആശയങ്ങളും ഉരുത്തിരിഞ്ഞ ഒരു ആശയപരമായ പ്രക്രിയയാണ് അതിന്റെ പ്രധാന അർത്ഥത്തിൽ അമൂർത്തീകരണം .
ഇതര ഹിപ് ഹോപ്പ്: മുഖ്യധാരയായി സാധാരണ തിരിച്ചറിയപ്പെടാത്ത വൈവിധ്യമാർന്ന ശൈലികൾ ഉൾക്കൊള്ളുന്ന ഹിപ് ഹോപ്പ് സംഗീതത്തിന്റെ ഉപവിഭാഗമാണ് ഇതര ഹിപ് ഹോപ്പ് . ഓൾ‌ മ്യൂസിക് ഇതിനെ ഇനിപ്പറയുന്ന രീതിയിൽ നിർ‌വ്വചിക്കുന്നു: "റാങ്‌സിന്റെ പരമ്പരാഗത സ്റ്റീരിയോടൈപ്പുകളായ ഗ്യാങ്‌സ്റ്റ, ബാസ്, ഹാർഡ്‌കോർ, പോപ്പ്, പാർട്ടി റാപ്പ് എന്നിവയുമായി പൊരുത്തപ്പെടാൻ വിസമ്മതിക്കുന്ന ഹിപ് ഹോപ്പ് ഗ്രൂപ്പുകളെയാണ് ഇതര റാപ്പ് എന്ന് പറയുന്നത്. പകരം, ഫങ്കിൽ നിന്ന് തുല്യമായി വരയ്ക്കുന്ന വിഭാഗങ്ങളെ അവ്യക്തമാക്കുന്നു. പോപ്പ് / റോക്ക്, ജാസ്, സോൾ, റെഗ്ഗെ, നാടോടി എന്നിവയും.
സംഗ്രഹം: നിർദ്ദിഷ്ട ഉദാഹരണങ്ങൾ, അക്ഷര സൂചകങ്ങൾ, ആദ്യ തത്ത്വങ്ങൾ അല്ലെങ്കിൽ മറ്റ് രീതികളുടെ ഉപയോഗത്തിൽ നിന്നും വർഗ്ഗീകരണത്തിൽ നിന്നും പൊതുവായ നിയമങ്ങളും ആശയങ്ങളും ഉരുത്തിരിഞ്ഞ ഒരു ആശയപരമായ പ്രക്രിയയാണ് അതിന്റെ പ്രധാന അർത്ഥത്തിൽ അമൂർത്തീകരണം .
അമൂർത്ത വ്യാഖ്യാനം: കമ്പ്യൂട്ടർ സയൻസിൽ, ഓർഡർ ചെയ്ത സെറ്റുകളിൽ, പ്രത്യേകിച്ച് ലാറ്റിസുകളിൽ മോണോടോണിക് ഫംഗ്ഷനുകളെ അടിസ്ഥാനമാക്കി കമ്പ്യൂട്ടർ പ്രോഗ്രാമുകളുടെ സെമാന്റിക്സിന്റെ ശബ്ദ ഏകദേശ സിദ്ധാന്തമാണ് അമൂർത്ത വ്യാഖ്യാനം . എല്ലാ കണക്കുകൂട്ടലുകളും നടത്താതെ തന്നെ അതിന്റെ അർത്ഥശാസ്ത്രത്തെക്കുറിച്ചുള്ള വിവരങ്ങൾ നേടുന്ന ഒരു കമ്പ്യൂട്ടർ പ്രോഗ്രാമിന്റെ ഭാഗിക നിർവ്വഹണമായി ഇതിനെ കാണാൻ കഴിയും.
അമൂർത്ത മാറ്റിയെഴുത്ത് സംവിധാനം: മാത്തമാറ്റിക്കൽ ലോജിക്, സൈദ്ധാന്തിക കമ്പ്യൂട്ടർ സയൻസ് എന്നിവയിൽ, അമൂർത്തമായ മാറ്റിയെഴുതൽ സംവിധാനം എന്നത് formal പചാരികതയാണ്. അതിന്റെ ലളിതമായ രൂപത്തിൽ, ARS എന്നത് ഒരു ബൈനറി ബന്ധമുള്ള പരമ്പരാഗതമായി സൂചിപ്പിച്ചിരിക്കുന്ന ഒരു കൂട്ടമാണ് ; ബൈനറി റിലേഷന്റെ സബ്സെറ്റുകൾ സൂചിക (ലേബൽ) ചെയ്താൽ ഈ നിർവചനം കൂടുതൽ പരിഷ്കരിക്കാനാകും. ലളിതത ഉണ്ടായിരുന്നിട്ടും, സാധാരണ രൂപങ്ങൾ, അവസാനിപ്പിക്കൽ, സംഗമത്തിന്റെ വിവിധ സങ്കൽപ്പങ്ങൾ എന്നിവ പോലുള്ള മാറ്റിയെഴുതൽ സംവിധാനങ്ങളുടെ പ്രധാന സവിശേഷതകൾ വിവരിക്കാൻ ഒരു ARS പര്യാപ്തമാണ്.
അമൂർത്ത പോളിറ്റോപ്പ്: ഗണിതശാസ്ത്രത്തിൽ, ഒരു ബീജഗണിതം ഭാഗികമായി ക്രമീകരിച്ച ഒരു സെറ്റ് അല്ലെങ്കിൽ പോസെറ്റാണ് അമൂർത്ത പോളിറ്റോപ്പ് , ഇത് പരമ്പരാഗത പോളിറ്റോപ്പിന്റെ കോമ്പിനേറ്റോറിയൽ ഗുണങ്ങളെ കോണുകൾ അല്ലെങ്കിൽ എഡ്ജ് ദൈർഘ്യം പോലുള്ള ജ്യാമിതീയ സവിശേഷതകൾ വ്യക്തമാക്കാതെ പിടിച്ചെടുക്കുന്നു. പോളിഗോപ്പ്, പോളിഹെഡ്ര എന്നിവയെ എത്ര അളവുകളിലേക്ക് സാമാന്യവൽക്കരിക്കുന്നു.
അമൂർത്ത പോളിറ്റോപ്പ്: ഗണിതശാസ്ത്രത്തിൽ, ഒരു ബീജഗണിതം ഭാഗികമായി ക്രമീകരിച്ച ഒരു സെറ്റ് അല്ലെങ്കിൽ പോസെറ്റാണ് അമൂർത്ത പോളിറ്റോപ്പ് , ഇത് പരമ്പരാഗത പോളിറ്റോപ്പിന്റെ കോമ്പിനേറ്റോറിയൽ ഗുണങ്ങളെ കോണുകൾ അല്ലെങ്കിൽ എഡ്ജ് ദൈർഘ്യം പോലുള്ള ജ്യാമിതീയ സവിശേഷതകൾ വ്യക്തമാക്കാതെ പിടിച്ചെടുക്കുന്നു. പോളിഗോപ്പ്, പോളിഹെഡ്ര എന്നിവയെ എത്ര അളവുകളിലേക്ക് സാമാന്യവൽക്കരിക്കുന്നു.
റഫറൻസ് ചോദ്യം: കനേഡിയൻ നിയമത്തിൽ, ഒരു റഫറൻസ് ചോദ്യം അല്ലെങ്കിൽ റഫറൻസ് കേസ് ഒരു പ്രധാന നിയമപ്രശ്നത്തെക്കുറിച്ച് ഉപദേശക അഭിപ്രായം ആവശ്യപ്പെട്ട് ഫെഡറൽ അല്ലെങ്കിൽ ഒരു പ്രവിശ്യാ ഗവൺമെന്റ് കോടതികൾക്ക് സമർപ്പിക്കുന്നതാണ്. സാധാരണ ചോദ്യം നിയമനിർമ്മാണത്തിന്റെ ഭരണഘടനയെക്കുറിച്ചാണ്.
അമൂർത്ത മാറ്റിയെഴുത്ത് സംവിധാനം: മാത്തമാറ്റിക്കൽ ലോജിക്, സൈദ്ധാന്തിക കമ്പ്യൂട്ടർ സയൻസ് എന്നിവയിൽ, അമൂർത്തമായ മാറ്റിയെഴുതൽ സംവിധാനം എന്നത് formal പചാരികതയാണ്. അതിന്റെ ലളിതമായ രൂപത്തിൽ, ARS എന്നത് ഒരു ബൈനറി ബന്ധമുള്ള പരമ്പരാഗതമായി സൂചിപ്പിച്ചിരിക്കുന്ന ഒരു കൂട്ടമാണ് ; ബൈനറി റിലേഷന്റെ സബ്സെറ്റുകൾ സൂചിക (ലേബൽ) ചെയ്താൽ ഈ നിർവചനം കൂടുതൽ പരിഷ്കരിക്കാനാകും. ലളിതത ഉണ്ടായിരുന്നിട്ടും, സാധാരണ രൂപങ്ങൾ, അവസാനിപ്പിക്കൽ, സംഗമത്തിന്റെ വിവിധ സങ്കൽപ്പങ്ങൾ എന്നിവ പോലുള്ള മാറ്റിയെഴുതൽ സംവിധാനങ്ങളുടെ പ്രധാന സവിശേഷതകൾ വിവരിക്കാൻ ഒരു ARS പര്യാപ്തമാണ്.
അമൂർത്ത മാറ്റിയെഴുത്ത് സംവിധാനം: മാത്തമാറ്റിക്കൽ ലോജിക്, സൈദ്ധാന്തിക കമ്പ്യൂട്ടർ സയൻസ് എന്നിവയിൽ, അമൂർത്തമായ മാറ്റിയെഴുതൽ സംവിധാനം എന്നത് formal പചാരികതയാണ്. അതിന്റെ ലളിതമായ രൂപത്തിൽ, ARS എന്നത് ഒരു ബൈനറി ബന്ധമുള്ള പരമ്പരാഗതമായി സൂചിപ്പിച്ചിരിക്കുന്ന ഒരു കൂട്ടമാണ് ; ബൈനറി റിലേഷന്റെ സബ്സെറ്റുകൾ സൂചിക (ലേബൽ) ചെയ്താൽ ഈ നിർവചനം കൂടുതൽ പരിഷ്കരിക്കാനാകും. ലളിതത ഉണ്ടായിരുന്നിട്ടും, സാധാരണ രൂപങ്ങൾ, അവസാനിപ്പിക്കൽ, സംഗമത്തിന്റെ വിവിധ സങ്കൽപ്പങ്ങൾ എന്നിവ പോലുള്ള മാറ്റിയെഴുതൽ സംവിധാനങ്ങളുടെ പ്രധാന സവിശേഷതകൾ വിവരിക്കാൻ ഒരു ARS പര്യാപ്തമാണ്.
അമൂർത്ത മാറ്റിയെഴുത്ത് യന്ത്രം: ചുരുങ്ങിയ ടേം റീറൈറ്റിംഗ് സിസ്റ്റങ്ങൾക്കായി ടേം റീറൈറ്റിംഗ് നടപ്പിലാക്കുന്ന ഒരു വെർച്വൽ മെഷീനാണ് അബ്‌സ്ട്രാക്റ്റ് റീറൈറ്റിംഗ് മെഷീൻ (ARM).
അമൂർത്ത മാറ്റിയെഴുത്ത് സംവിധാനം: മാത്തമാറ്റിക്കൽ ലോജിക്, സൈദ്ധാന്തിക കമ്പ്യൂട്ടർ സയൻസ് എന്നിവയിൽ, അമൂർത്തമായ മാറ്റിയെഴുതൽ സംവിധാനം എന്നത് formal പചാരികതയാണ്. അതിന്റെ ലളിതമായ രൂപത്തിൽ, ARS എന്നത് ഒരു ബൈനറി ബന്ധമുള്ള പരമ്പരാഗതമായി സൂചിപ്പിച്ചിരിക്കുന്ന ഒരു കൂട്ടമാണ് ; ബൈനറി റിലേഷന്റെ സബ്സെറ്റുകൾ സൂചിക (ലേബൽ) ചെയ്താൽ ഈ നിർവചനം കൂടുതൽ പരിഷ്കരിക്കാനാകും. ലളിതത ഉണ്ടായിരുന്നിട്ടും, സാധാരണ രൂപങ്ങൾ, അവസാനിപ്പിക്കൽ, സംഗമത്തിന്റെ വിവിധ സങ്കൽപ്പങ്ങൾ എന്നിവ പോലുള്ള മാറ്റിയെഴുതൽ സംവിധാനങ്ങളുടെ പ്രധാന സവിശേഷതകൾ വിവരിക്കാൻ ഒരു ARS പര്യാപ്തമാണ്.
ആധുനിക ശില്പം: ആധുനിക ശില്പത്തിന്റെ തുടക്കക്കാരനായി കാണപ്പെടുന്ന അഗസ്റ്റെ റോഡിൻറെ സൃഷ്ടികളിലൂടെയാണ് ആധുനിക ശില്പം പൊതുവേ കണക്കാക്കപ്പെടുന്നത്. റോഡിൻ ഭൂതകാലത്തിനെതിരെ മത്സരിക്കാൻ തയ്യാറായില്ലെങ്കിലും, തന്റെ കൃതികൾ കെട്ടിപ്പടുക്കുന്നതിനുള്ള ഒരു പുതിയ മാർഗം അദ്ദേഹം സൃഷ്ടിച്ചു. "സമകാലിക നിയോ-ഗ്രീക്ക് അക്കാദമിസത്തിന്റെ കർശനമായ രൂപരേഖ അദ്ദേഹം അലിയിച്ചു, അതുവഴി അതാര്യതയുടെയും സുതാര്യതയുടെയും അളവ്, ശൂന്യത എന്നിവയുടെ സുപ്രധാന സമന്വയം സൃഷ്ടിച്ചു". പത്തൊൻപതാം നൂറ്റാണ്ടിന്റെ അവസാനത്തിൽ എഡ്ഗർ ഡെഗാസ്, പോൾ ഗ ugu ഗ്വിൻ തുടങ്ങിയ ശില്പകലയിൽ പുതിയ കലാപരമായ ദർശനങ്ങൾ പരീക്ഷിച്ച മറ്റ് ചില കലാകാരന്മാർക്കൊപ്പം റോഡിൻ ശില്പനിർമ്മാണത്തിൽ സമൂലമായ ഒരു പുതിയ സമീപനം കണ്ടുപിടിച്ചു. ആധുനിക ശില്പം, എല്ലാ ആധുനിക കലകളോടും കൂടി, "പത്തൊൻപതാം നൂറ്റാണ്ടിൽ ഉയർന്നുവന്ന നഗര, വ്യാവസായിക, മതേതര സമൂഹവുമായി പൊരുത്തപ്പെടാനുള്ള പാശ്ചാത്യ സമൂഹത്തിന്റെ ശ്രമത്തിന്റെ ഭാഗമായി ഉയർന്നുവന്നു".
അമൂർത്ത സെമാന്റിക് ഗ്രാഫ്: കമ്പ്യൂട്ടർ സയൻസിൽ, ഒരു അമൂർത്തമായ സെമാന്റിക് ഗ്രാഫ് ( എ.എസ്.ജി ) അല്ലെങ്കിൽ ടേം ഗ്രാഫ് എന്നത് ഒരു അമൂർത്ത വാക്യഘടനയാണ്, അതിൽ formal പചാരിക അല്ലെങ്കിൽ പ്രോഗ്രാമിംഗ് ഭാഷയുടെ ഒരു പദപ്രയോഗത്തെ പ്രതിനിധീകരിക്കുന്ന ഒരു ഗ്രാഫ് പ്രതിനിധീകരിക്കുന്നു. ഒരു എ‌എസ്‌ജി ഒരു അമൂർത്ത വാക്യഘടനയെക്കാൾ ഉയർന്ന തലത്തിലുള്ള അമൂർത്തമാണ്, ഇത് ഒരു പദപ്രയോഗത്തിന്റെയോ പ്രോഗ്രാമിന്റെയോ വാക്യഘടനയെ പ്രകടിപ്പിക്കാൻ ഉപയോഗിക്കുന്നു.
സെൻസ് ഡാറ്റ: ഇരുപതാം നൂറ്റാണ്ടിന്റെ തുടക്കത്തിൽ ബെർട്രാൻഡ് റസ്സൽ, സിഡി ബ്രോഡ്, എച്ച് എച്ച് പ്രൈസ്, എ ജെ അയർ, ജി ഇ മൂർ തുടങ്ങിയ തത്ത്വചിന്തകർ പ്രചാരത്തിലുണ്ടായിരുന്ന ഗർഭധാരണ തത്ത്വചിന്തയിലെ ഒരു കാഴ്ചയാണ് സെൻസ് ഡാറ്റയുടെ സിദ്ധാന്തം. ഇന്ദ്രിയ ഡാറ്റയെ മനസ്സിനെ ആശ്രയിച്ചുള്ള വസ്‌തുക്കളായി കണക്കാക്കുന്നു, അവയുടെ നിലനിൽപ്പും ഗുണങ്ങളും ഗർഭധാരണത്തിൽ നമുക്ക് നേരിട്ട് അറിയാം. ഈ വസ്‌തുക്കൾ മനസിനുള്ളിലെ വിശകലനം ചെയ്യാത്ത അനുഭവങ്ങളാണ്, അവ തുടർന്നുള്ള കൂടുതൽ വിപുലമായ മാനസിക പ്രവർത്തനങ്ങൾക്ക് ദൃശ്യമാകുന്നു.
സിദ്ധാന്തം സജ്ജമാക്കുക: ഗണിതശാസ്ത്ര യുക്തിയുടെ ഒരു ശാഖയാണ് സെറ്റ് തിയറി , അത് സെറ്റുകൾ പഠിക്കുന്നു, അവ അന infor പചാരികമായി വസ്തുക്കളുടെ ശേഖരമാണ്. ഏത് തരത്തിലുള്ള ഒബ്ജക്റ്റുകളും ഒരു സെറ്റിലേക്ക് ശേഖരിക്കാമെങ്കിലും, ഗണിതശാസ്ത്രത്തിന് പ്രസക്തമായ വസ്തുക്കളിൽ സെറ്റ് തിയറി മിക്കപ്പോഴും പ്രയോഗിക്കുന്നു. മിക്കവാറും എല്ലാ ഗണിത വസ്തുക്കളെയും നിർവചിക്കാൻ സെറ്റ് തിയറിയുടെ ഭാഷ ഉപയോഗിക്കാം.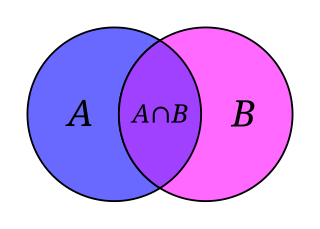
അമൂർത്ത ലളിതമായ സങ്കീർണ്ണത: കോമ്പിനേറ്ററിക്സിൽ, ഒരു അമൂർത്ത സിംപ്ലിസിയൽ കോംപ്ലക്സ് (എ‌എസ്‌സി) എന്നത് ഒരു കൂട്ടം സെറ്റുകളാണ്, അത് ഉപസെറ്റുകൾ എടുക്കുന്നതിനനുസരിച്ച് അടച്ചിരിക്കുന്നു, അതായത്, കുടുംബത്തിലെ ഒരു സെറ്റിന്റെ എല്ലാ ഉപസെറ്റുകളും കുടുംബത്തിലുണ്ട്. ലളിതമായ ഒരു സമുച്ചയത്തിന്റെ ജ്യാമിതീയ സങ്കൽപ്പത്തിന്റെ പൂർണ്ണമായും സംയോജിത വിവരണമാണിത്. ഉദാഹരണത്തിന്, ഒരു ദ്വിമാന ലളിതമായ സമുച്ചയത്തിൽ, കുടുംബത്തിലെ സെറ്റുകൾ ത്രികോണങ്ങൾ, അവയുടെ അരികുകൾ, അവയുടെ ലംബങ്ങൾ എന്നിവയാണ്.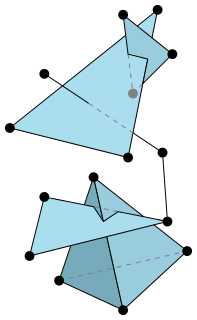
അമൂർത്തമായ ഇടം: ഭൂമിശാസ്ത്രത്തിൽ അമൂർത്തമായ ഇടം എന്നത് തുല്യവും സ്ഥിരവുമായ സവിശേഷതകളാൽ ചിത്രീകരിക്കപ്പെടുന്ന ഒരു സാങ്കൽപ്പിക ഇടമാണ്; പൂർണ്ണമായും ഏകതാനമായ ഒരു ഭൂമിശാസ്ത്രപരമായ ഇടം. എല്ലാ ചലനങ്ങളും പ്രവർത്തനങ്ങളും എല്ലാ ദിശകളിലും ഈ സ്ഥലത്തിനുള്ളിലെ എല്ലാ സ്ഥലങ്ങളിലും ഒരുപോലെ എളുപ്പമോ ബുദ്ധിമുട്ടുള്ളതോ ആയിരിക്കും. ഭൂപ്രദേശം പോലുള്ള ബാഹ്യ വേരിയബിളുകളെ പരിമിതപ്പെടുത്തുകയോ ഒഴിവാക്കുകയോ ചെയ്യുന്നതിലൂടെ സ്പേഷ്യൽ പ്രവർത്തനവും പെരുമാറ്റവും മോഡലിംഗ് ചെയ്യുന്നതിനോ വിശകലനം ചെയ്യുന്നതിനോ ഈ ആശയം ഉപയോഗപ്രദമാണ്. ഉദാഹരണത്തിന്, ഗവേഷകർ സംസ്കാരവും വ്യാപാരവും തമ്മിലുള്ള ബന്ധത്തെക്കുറിച്ച് പഠിക്കാൻ ആഗ്രഹിക്കുന്നുവെങ്കിൽ, അവരുടെ മാതൃക പർവതനിരകളിലെ തടസ്സങ്ങളും നദികളും പോലുള്ള ഘടകങ്ങളാൽ സ്വാധീനിക്കപ്പെടാനോ സ്വാധീനിക്കാനോ അവർ ആഗ്രഹിക്കുന്നില്ല, കാരണം സംസ്കാരം മാത്രം വ്യാപാരത്തെ എങ്ങനെ സ്വാധീനിക്കുന്നു എന്നതിന്റെ ഉദ്ദേശ്യത്തിൽ നിന്ന് ഇത് വ്യതിചലിക്കും.
അമൂർത്ത സ്റ്റേറ്റ് മെഷീൻ: കമ്പ്യൂട്ടർ സയൻസിൽ, അനിയന്ത്രിതമായ ഡാറ്റാ ഘടനകളുള്ള സംസ്ഥാനങ്ങളിൽ പ്രവർത്തിക്കുന്ന ഒരു സ്റ്റേറ്റ് മെഷീനാണ് അമൂർത്ത സ്റ്റേറ്റ് മെഷീൻ ( ASM ).
അമൂർത്ത സ്റ്റേറ്റ് മെഷീൻ: കമ്പ്യൂട്ടർ സയൻസിൽ, അനിയന്ത്രിതമായ ഡാറ്റാ ഘടനകളുള്ള സംസ്ഥാനങ്ങളിൽ പ്രവർത്തിക്കുന്ന ഒരു സ്റ്റേറ്റ് മെഷീനാണ് അമൂർത്ത സ്റ്റേറ്റ് മെഷീൻ ( ASM ).
അമൂർത്ത സ്റ്റേറ്റ് മെഷീൻ: കമ്പ്യൂട്ടർ സയൻസിൽ, അനിയന്ത്രിതമായ ഡാറ്റാ ഘടനകളുള്ള സംസ്ഥാനങ്ങളിൽ പ്രവർത്തിക്കുന്ന ഒരു സ്റ്റേറ്റ് മെഷീനാണ് അമൂർത്ത സ്റ്റേറ്റ് മെഷീൻ ( ASM ).
അമൂർത്ത തന്ത്ര ഗെയിം: കളിയുടെ അനുഭവത്തിന് തീം പ്രധാനമല്ലാത്ത ഒരു തന്ത്ര ഗെയിമാണ് അമൂർത്ത തന്ത്ര ഗെയിം . ലോകത്തെ പല ക്ലാസിക് ബോർഡ് ഗെയിമുകളായ ചെസ്സ്, ഗോ, ചെക്കറുകളും ഡ്രാഫ്റ്റുകളും, സിയാങ്‌കി, ഷോഗി, റിവേർ‌സി, ഒൻപത് പുരുഷന്മാരുടെ മോറിസ്, മിക്ക മങ്കാല വേരിയന്റുകളും ഈ വിഭാഗത്തിൽ‌ ഉൾ‌പ്പെടുന്നു, ഡാമിയോ, ഹൈവ്, യിൻ‌ഷ് എന്നിവപോലുള്ള ആധുനിക ആവർത്തനങ്ങൾ‌ പോലെ .
അമൂർത്ത തന്ത്ര ഗെയിം: കളിയുടെ അനുഭവത്തിന് തീം പ്രധാനമല്ലാത്ത ഒരു തന്ത്ര ഗെയിമാണ് അമൂർത്ത തന്ത്ര ഗെയിം . ലോകത്തെ പല ക്ലാസിക് ബോർഡ് ഗെയിമുകളായ ചെസ്സ്, ഗോ, ചെക്കറുകളും ഡ്രാഫ്റ്റുകളും, സിയാങ്‌കി, ഷോഗി, റിവേർ‌സി, ഒൻപത് പുരുഷന്മാരുടെ മോറിസ്, മിക്ക മങ്കാല വേരിയന്റുകളും ഈ വിഭാഗത്തിൽ‌ ഉൾ‌പ്പെടുന്നു, ഡാമിയോ, ഹൈവ്, യിൻ‌ഷ് എന്നിവപോലുള്ള ആധുനിക ആവർത്തനങ്ങൾ‌ പോലെ .
അമൂർത്ത തന്ത്ര ഗെയിം: കളിയുടെ അനുഭവത്തിന് തീം പ്രധാനമല്ലാത്ത ഒരു തന്ത്ര ഗെയിമാണ് അമൂർത്ത തന്ത്ര ഗെയിം . ലോകത്തെ പല ക്ലാസിക് ബോർഡ് ഗെയിമുകളായ ചെസ്സ്, ഗോ, ചെക്കറുകളും ഡ്രാഫ്റ്റുകളും, സിയാങ്‌കി, ഷോഗി, റിവേർ‌സി, ഒൻപത് പുരുഷന്മാരുടെ മോറിസ്, മിക്ക മങ്കാല വേരിയന്റുകളും ഈ വിഭാഗത്തിൽ‌ ഉൾ‌പ്പെടുന്നു, ഡാമിയോ, ഹൈവ്, യിൻ‌ഷ് എന്നിവപോലുള്ള ആധുനിക ആവർത്തനങ്ങൾ‌ പോലെ .
അമൂർത്ത തന്ത്ര ഗെയിം: കളിയുടെ അനുഭവത്തിന് തീം പ്രധാനമല്ലാത്ത ഒരു തന്ത്ര ഗെയിമാണ് അമൂർത്ത തന്ത്ര ഗെയിം . ലോകത്തെ പല ക്ലാസിക് ബോർഡ് ഗെയിമുകളായ ചെസ്സ്, ഗോ, ചെക്കറുകളും ഡ്രാഫ്റ്റുകളും, സിയാങ്‌കി, ഷോഗി, റിവേർ‌സി, ഒൻപത് പുരുഷന്മാരുടെ മോറിസ്, മിക്ക മങ്കാല വേരിയന്റുകളും ഈ വിഭാഗത്തിൽ‌ ഉൾ‌പ്പെടുന്നു, ഡാമിയോ, ഹൈവ്, യിൻ‌ഷ് എന്നിവപോലുള്ള ആധുനിക ആവർത്തനങ്ങൾ‌ പോലെ .
ഘടനാപരമായ (ഗണിതശാസ്ത്രത്തിന്റെ തത്ത്വചിന്ത): ഗണിതശാസ്ത്ര തത്ത്വചിന്തയിലെ ഒരു സിദ്ധാന്തമാണ് സ്ട്രക്ചറലിസം , ഗണിതശാസ്ത്ര സിദ്ധാന്തങ്ങൾ ഗണിത വസ്തുക്കളുടെ ഘടനയെ വിവരിക്കുന്നു. ഗണിത വസ്‌തുക്കൾ അത്തരം ഘടനകളിലെ അവയുടെ സ്ഥാനം ഉപയോഗിച്ച് സമഗ്രമായി നിർവചിക്കപ്പെടുന്നു. തന്മൂലം, ഗണിതവസ്തുക്കൾക്ക് അന്തർലീനമായ ഗുണങ്ങളൊന്നുമില്ലെന്നും എന്നാൽ ഒരു സിസ്റ്റത്തിലെ അവയുടെ ബാഹ്യ ബന്ധങ്ങളാൽ നിർവചിക്കപ്പെടുന്നുവെന്നും ഘടനാപരമായ വാദം നിലനിൽക്കുന്നു. ഉദാഹരണത്തിന്, സ്വാഭാവിക സംഖ്യകളുടെ സിദ്ധാന്തത്തിന്റെ ഘടനയിൽ 0 ന്റെ പിൻഗാമിയായി നമ്പർ 1 സമഗ്രമായി നിർവചിക്കപ്പെടുന്നുവെന്ന് ഘടനാപരമായ വാദം. ഈ ഉദാഹരണത്തിന്റെ സാമാന്യവൽക്കരണത്തിലൂടെ, ഏതൊരു സ്വാഭാവിക സംഖ്യയെയും നമ്പർ വരിയുടെ ഈ ഘടനയിൽ അതത് സ്ഥലത്താൽ നിർവചിക്കുന്നു. ഗണിത വസ്‌തുക്കളുടെ മറ്റ് ഉദാഹരണങ്ങളിൽ ജ്യാമിതിയിലെ വരികളും വിമാനങ്ങളും അല്ലെങ്കിൽ അമൂർത്ത ബീജഗണിതത്തിലെ ഘടകങ്ങളും പ്രവർത്തനങ്ങളും ഉൾപ്പെടാം.
അമൂർത്ത ഘടന: ഒരു അമൂർത്ത ഘടന എന്നത് ഒരു formal പചാരിക വസ്തുവാണ്, അത് ഒരു കൂട്ടം നിയമങ്ങൾ, സ്വത്തുക്കൾ, ബന്ധങ്ങൾ എന്നിവയാൽ നിർവചിക്കപ്പെടുന്നു, അത് യുക്തിപരമായി എല്ലായ്പ്പോഴും ചരിത്രപരമായ അനിശ്ചിത അനുഭവങ്ങളുടെ ഘടനയിൽ നിന്ന് സ്വതന്ത്രമല്ലെങ്കിൽ, ഉദാഹരണത്തിന്, ഭ physical തിക വസ്തുക്കൾ ഉൾപ്പെടുന്നവ. അമൂർത്ത ഘടനകളെ യുക്തിയിലും ഗണിതത്തിലും മാത്രമല്ല, കമ്പ്യൂട്ടർ സയൻസ് എന്ന നിലയിലും തത്ത്വചിന്ത പോലുള്ള പ്രതിഫലിപ്പിക്കുന്ന പഠനങ്ങളിലും പഠിക്കുന്നു. ആധുനിക ഗണിതശാസ്ത്രത്തെ പൊതുവായ അർത്ഥത്തിൽ അമൂർത്ത ഘടനകളെക്കുറിച്ചുള്ള പഠനമായി നിർവചിച്ചിരിക്കുന്നു.
അമൂർത്ത മാനേജുമെന്റ്: ഒരു അക്കാദമിക് കോൺഫറൻസിൽ അവതരണത്തിനായി സംഗ്രഹങ്ങൾ സ്വീകരിക്കുകയും തയ്യാറാക്കുകയും ചെയ്യുന്ന പ്രക്രിയയാണ് അമൂർത്ത മാനേജുമെന്റ് . ജോലിയുടെ അമൂർത്തമായ അല്ലെങ്കിൽ സംഗ്രഹത്തിന്റെ ക്ഷണിക്കപ്പെട്ട അല്ലെങ്കിൽ ലാഭകരമായ സമർപ്പിക്കലുകൾ ഈ പ്രക്രിയയിൽ അടങ്ങിയിരിക്കുന്നു. സംക്ഷിപ്തം, ഗവേഷണത്തിലോ അന്വേഷണത്തിലോ ഉപയോഗിക്കുന്ന ഉപകരണങ്ങൾ, ശേഖരിച്ച ഡാറ്റ, ഡാറ്റയുടെ സംഗ്രഹം അല്ലെങ്കിൽ വ്യാഖ്യാനം എന്നിവ അമൂർത്തത്തിൽ സാധാരണ പറയുന്നു.
ക്ലാസ് (കമ്പ്യൂട്ടർ പ്രോഗ്രാമിംഗ്): ഒബ്ജക്റ്റ്-ഓറിയന്റഡ് പ്രോഗ്രാമിംഗിൽ, ഒബ്ജക്റ്റുകൾ സൃഷ്ടിക്കുന്നതിനും സംസ്ഥാനത്തിന് പ്രാരംഭ മൂല്യങ്ങൾ നൽകുന്നതിനും പെരുമാറ്റത്തിന്റെ നടപ്പാക്കലിനുമുള്ള വിപുലീകരിക്കാവുന്ന പ്രോഗ്രാം-കോഡ്-ടെംപ്ലേറ്റാണ് ക്ലാസ് . പല ഭാഷകളിലും, ക്ലാസ് നാമം ക്ലാസിന്റെ പേരായും ക്ലാസിന്റെ സ്ഥിരസ്ഥിതി കൺ‌സ്‌ട്രക്റ്ററുടെ പേരായും ക്ലാസ് ഇൻസ്റ്റാളുചെയ്യുന്നതിലൂടെ സൃഷ്ടിക്കുന്ന ഒബ്‌ജക്റ്റുകളുടെ പേരായും ഉപയോഗിക്കുന്നു; ഈ വ്യതിരിക്തമായ ആശയങ്ങൾ എളുപ്പത്തിൽ പരസ്പരം ബന്ധപ്പെട്ടിരിക്കുന്നു. ആശയക്കുഴപ്പത്തിന്റെ ഘട്ടത്തിൽ, ഒരു ഭാഷയിൽ അതിന്റെ സ്വഭാവ സവിശേഷത കാരണം ഒരു ഭാഷയിൽ അന്തർലീനമായ ഒരു സവിശേഷതയാണെന്നും പോളിമോർഫിസം ഇല്ലാത്ത ഭാഷകളുമായി താരതമ്യപ്പെടുത്തുമ്പോൾ ഈ ഭാഷകൾ എന്തിനാണ് ശക്തവും ചലനാത്മകവും ഉപയോഗത്തിന് അനുയോജ്യവുമാണെന്നും വാദിക്കാൻ കഴിയുന്നത്. അതിനാൽ അവർക്ക് ചലനാത്മക സംവിധാനങ്ങളെ കൂടുതൽ എളുപ്പത്തിൽ മാതൃകയാക്കാൻ കഴിയും.
അമൂർത്ത വാക്യഘടന: കമ്പ്യൂട്ടർ സയൻസിൽ, ഏതെങ്കിലും പ്രത്യേക പ്രാതിനിധ്യത്തിൽ നിന്നോ എൻകോഡിംഗിൽ നിന്നോ വിഭിന്നമായി ഡാറ്റാ തരമായി വിവരിച്ചിരിക്കുന്ന അതിന്റെ ഘടനയാണ് ഡാറ്റയുടെ അമൂർത്ത വാക്യഘടന . കമ്പ്യൂട്ടർ ഭാഷകളിലെ വാചകത്തിന്റെ പ്രാതിനിധ്യത്തിൽ ഇത് പ്രത്യേകിച്ചും ഉപയോഗിക്കുന്നു, അവ സാധാരണയായി ഒരു ട്രീ ഘടനയിൽ ഒരു അമൂർത്ത വാക്യഘടന ട്രീ ആയി സൂക്ഷിക്കുന്നു. ഡാറ്റയുടെ ഘടന മാത്രം ഉൾക്കൊള്ളുന്ന അമൂർത്ത വാക്യഘടന കോൺക്രീറ്റ് വാക്യഘടനയുമായി വിഭിന്നമാണ്, അതിൽ പ്രാതിനിധ്യത്തെക്കുറിച്ചുള്ള വിവരങ്ങളും ഉൾപ്പെടുന്നു. ഉദാഹരണത്തിന്, കോൺക്രീറ്റ് വാക്യഘടനയിൽ പരാൻതീസിസ് അല്ലെങ്കിൽ കോമ പോലുള്ള സവിശേഷതകൾ ഉൾപ്പെടുന്നു, അവ അമൂർത്ത വാക്യഘടനയിൽ ഉൾപ്പെടുത്തിയിട്ടില്ല, കാരണം അവ ഘടനയിൽ ഉൾക്കൊള്ളുന്നു.
ASN.1: ക്രോസ്-പ്ലാറ്റ്ഫോം രീതിയിൽ സീരിയലൈസ് ചെയ്യാനും ഡിസീരിയലൈസ് ചെയ്യാനും കഴിയുന്ന ഡാറ്റാ ഘടനകളെ നിർവചിക്കുന്നതിനുള്ള ഒരു സ്റ്റാൻഡേർഡ് ഇന്റർഫേസ് വിവരണ ഭാഷയാണ് അമൂർത്ത സിന്റാക്സ് നൊട്ടേഷൻ വൺ ( ASN.1 ). ടെലികമ്മ്യൂണിക്കേഷൻ, കമ്പ്യൂട്ടർ നെറ്റ്‌വർക്കിംഗ്, പ്രത്യേകിച്ച് ക്രിപ്റ്റോഗ്രഫി എന്നിവയിൽ ഇത് വ്യാപകമായി ഉപയോഗിക്കുന്നു.
ASN.1: ക്രോസ്-പ്ലാറ്റ്ഫോം രീതിയിൽ സീരിയലൈസ് ചെയ്യാനും ഡിസീരിയലൈസ് ചെയ്യാനും കഴിയുന്ന ഡാറ്റാ ഘടനകളെ നിർവചിക്കുന്നതിനുള്ള ഒരു സ്റ്റാൻഡേർഡ് ഇന്റർഫേസ് വിവരണ ഭാഷയാണ് അമൂർത്ത സിന്റാക്സ് നൊട്ടേഷൻ വൺ ( ASN.1 ). ടെലികമ്മ്യൂണിക്കേഷൻ, കമ്പ്യൂട്ടർ നെറ്റ്‌വർക്കിംഗ്, പ്രത്യേകിച്ച് ക്രിപ്റ്റോഗ്രഫി എന്നിവയിൽ ഇത് വ്യാപകമായി ഉപയോഗിക്കുന്നു.
അമൂർത്ത വാക്യഘടന ട്രീ: കമ്പ്യൂട്ടർ സയൻസിൽ, ഒരു പ്രോഗ്രാമിംഗ് ഭാഷയിൽ എഴുതിയ സോഴ്‌സ് കോഡിന്റെ അമൂർത്ത വാക്യഘടനയുടെ ഒരു ട്രീ പ്രാതിനിധ്യമാണ് അമൂർത്ത സിന്റാക്സ് ട്രീ ( എഎസ്ടി ) അല്ലെങ്കിൽ സിന്റാക്സ് ട്രീ . ട്രീയുടെ ഓരോ നോഡും ഉറവിട കോഡിൽ സംഭവിക്കുന്ന ഒരു നിർമ്മാണത്തെ സൂചിപ്പിക്കുന്നു.
വ്യാഖ്യാതാവ് (കമ്പ്യൂട്ടിംഗ്): കമ്പ്യൂട്ടർ സയൻസിൽ, ഒരു മെഷീൻ ലാംഗ്വേജ് പ്രോഗ്രാമിലേക്ക് കംപൈൽ ചെയ്യേണ്ട ആവശ്യമില്ലാതെ, പ്രോഗ്രാമിംഗ് അല്ലെങ്കിൽ സ്ക്രിപ്റ്റിംഗ് ഭാഷയിൽ എഴുതിയ നിർദ്ദേശങ്ങൾ നേരിട്ട് നടപ്പിലാക്കുന്ന ഒരു കമ്പ്യൂട്ടർ പ്രോഗ്രാമാണ് ഇന്റർപ്രെറ്റർ . പ്രോഗ്രാം നിർവ്വഹണത്തിനായി ഒരു വ്യാഖ്യാതാവ് സാധാരണയായി ഇനിപ്പറയുന്ന തന്ത്രങ്ങളിലൊന്ന് ഉപയോഗിക്കുന്നു: ഉറവിട കോഡ് പാഴ്‌സുചെയ്‌ത് അതിന്റെ പെരുമാറ്റം നേരിട്ട് നടത്തുക; സോഴ്‌സ് കോഡ് ചില കാര്യക്ഷമമായ ഇന്റർമീഡിയറ്റ് പ്രാതിനിധ്യത്തിലേക്ക് വിവർത്തനം ചെയ്‌ത് ഉടൻ തന്നെ ഇത് നടപ്പിലാക്കുക; ഇന്റർപ്രെറ്റർ സിസ്റ്റത്തിന്റെ ഭാഗമായ ഒരു കംപൈലർ നിർമ്മിച്ച സംഭരിച്ച പ്രീ കംപൈൽ കോഡ് വ്യക്തമായി നടപ്പിലാക്കുക.
അമൂർത്ത വാക്യഘടന ട്രീ: കമ്പ്യൂട്ടർ സയൻസിൽ, ഒരു പ്രോഗ്രാമിംഗ് ഭാഷയിൽ എഴുതിയ സോഴ്‌സ് കോഡിന്റെ അമൂർത്ത വാക്യഘടനയുടെ ഒരു ട്രീ പ്രാതിനിധ്യമാണ് അമൂർത്ത സിന്റാക്സ് ട്രീ ( എഎസ്ടി ) അല്ലെങ്കിൽ സിന്റാക്സ് ട്രീ . ട്രീയുടെ ഓരോ നോഡും ഉറവിട കോഡിൽ സംഭവിക്കുന്ന ഒരു നിർമ്മാണത്തെ സൂചിപ്പിക്കുന്നു.
അമൂർത്ത വാക്യഘടന ട്രീ: കമ്പ്യൂട്ടർ സയൻസിൽ, ഒരു പ്രോഗ്രാമിംഗ് ഭാഷയിൽ എഴുതിയ സോഴ്‌സ് കോഡിന്റെ അമൂർത്ത വാക്യഘടനയുടെ ഒരു ട്രീ പ്രാതിനിധ്യമാണ് അമൂർത്ത സിന്റാക്സ് ട്രീ ( എഎസ്ടി ) അല്ലെങ്കിൽ സിന്റാക്സ് ട്രീ . ട്രീയുടെ ഓരോ നോഡും ഉറവിട കോഡിൽ സംഭവിക്കുന്ന ഒരു നിർമ്മാണത്തെ സൂചിപ്പിക്കുന്നു.
ടെസ്റ്റ് സ്യൂട്ട്: സോഫ്റ്റ്വെയർ ഡെവലപ്മെന്റിൽ, ഒരു ടെസ്റ്റ് സ്യൂട്ട് , 'മൂല്യനിർണ്ണയ സ്യൂട്ട്' എന്നറിയപ്പെടുന്ന ടെസ്റ്റ് കേസുകളുടെ ഒരു ശേഖരമാണ്, അത് ഒരു സോഫ്റ്റ്വെയർ പ്രോഗ്രാമിനെ പരീക്ഷിക്കാൻ ഉപയോഗിക്കാൻ ഉദ്ദേശിച്ചിട്ടുള്ള ടെസ്റ്റ് കേസുകളുടെ ഒരു ശേഖരമാണ്. ഒരു ടെസ്റ്റ് സ്യൂട്ടിൽ പലപ്പോഴും ടെസ്റ്റ് കേസുകളുടെ ഓരോ ശേഖരണത്തിനും വിശദമായ നിർദ്ദേശങ്ങളോ ലക്ഷ്യങ്ങളോ അടങ്ങിയിരിക്കുന്നു, കൂടാതെ പരിശോധന സമയത്ത് ഉപയോഗിക്കേണ്ട സിസ്റ്റം കോൺഫിഗറേഷനെക്കുറിച്ചുള്ള വിവരങ്ങളും. ഒരു കൂട്ടം ടെസ്റ്റ് കേസുകളിൽ മുൻ‌വ്യവസ്ഥകളും ഘട്ടങ്ങളും ഇനിപ്പറയുന്ന പരിശോധനകളുടെ വിവരണങ്ങളും അടങ്ങിയിരിക്കാം.
സംഗ്രഹം: നിർദ്ദിഷ്ട ഉദാഹരണങ്ങൾ, അക്ഷര സൂചകങ്ങൾ, ആദ്യ തത്ത്വങ്ങൾ അല്ലെങ്കിൽ മറ്റ് രീതികളുടെ ഉപയോഗത്തിൽ നിന്നും വർഗ്ഗീകരണത്തിൽ നിന്നും പൊതുവായ നിയമങ്ങളും ആശയങ്ങളും ഉരുത്തിരിഞ്ഞ ഒരു ആശയപരമായ പ്രക്രിയയാണ് അതിന്റെ പ്രധാന അർത്ഥത്തിൽ അമൂർത്തീകരണം .
സംഗ്രഹം: നിർദ്ദിഷ്ട ഉദാഹരണങ്ങൾ, അക്ഷര സൂചകങ്ങൾ, ആദ്യ തത്ത്വങ്ങൾ അല്ലെങ്കിൽ മറ്റ് രീതികളുടെ ഉപയോഗത്തിൽ നിന്നും വർഗ്ഗീകരണത്തിൽ നിന്നും പൊതുവായ നിയമങ്ങളും ആശയങ്ങളും ഉരുത്തിരിഞ്ഞ ഒരു ആശയപരമായ പ്രക്രിയയാണ് അതിന്റെ പ്രധാന അർത്ഥത്തിൽ അമൂർത്തീകരണം .