Inner Mongolia Normal University

ഇന്നർ മംഗോളിയ സാധാരണ സർവകലാശാല: ഓട്ടോണമസ് റീജിയൻ സർക്കാരിന്റെ അധികാരത്തിൻ കീഴിൽ പീപ്പിൾസ് റിപ്പബ്ലിക് ഓഫ് ചൈനയിലെ ഇന്നർ മംഗോളിയയിലെ ഒരു സർവ്വകലാശാലയാണ് ഇന്നർ മംഗോളിയ നോർമൽ യൂണിവേഴ്സിറ്റി . ഇന്നർ മംഗോളിയ സ്വയംഭരണ പ്രദേശത്തിന്റെ തലസ്ഥാന നഗരമായ ഹോഹോട്ടിലാണ് ഇത് സ്ഥിതിചെയ്യുന്നത്.
അനുബന്ധ പുതിയ ചിന്താ ശൃംഖല: കാലിഫോർണിയയിലെ പസഫിക് ഗ്രോവ് ആസ്ഥാനമായി പ്രവർത്തിക്കുന്ന അഫിലിയേറ്റഡ് ന്യൂ തോട്ട് നെറ്റ്വർക്ക് അഥവാ എഎൻ‌ടി‌എൻ 1992 ൽ സ്ഥാപിതമായ യുണൈറ്റഡ് സ്റ്റേറ്റ്സിലെ ന്യൂ തോട്ട് സെന്ററുകളുടെ ഒരു സംഘടനയാണ്. ഒരു സഹകരണ കൂട്ടായ്മയായി അംഗീകരിക്കപ്പെട്ട ഇത് ഒരു ഇൻട്രാഫെയ്ത്ത് ഓർഗനൈസേഷനാണ്. യഥാർത്ഥത്തിൽ സ്വതന്ത്ര മത ശാസ്ത്ര മന്ത്രിമാർക്ക്, ഇന്ന് അതിൽ എല്ലാത്തരം പുതിയ ചിന്താ സംഘടനകളും അഫിലിയേറ്റ് ചെയ്യാൻ ആഗ്രഹിക്കുന്ന വ്യക്തികളും ഉൾപ്പെടുന്നു.
ബോസ്റ്റൺ ഗ്ലോബ്: മസാച്യുസെറ്റ്സിലെ ബോസ്റ്റൺ ആസ്ഥാനമാക്കി പ്രവർത്തിക്കുന്ന ഒരു അമേരിക്കൻ ദിനപത്രമാണ് ബോസ്റ്റൺ ഗ്ലോബ് . പത്രം മൊത്തം 26 പുലിറ്റ്‌സർ സമ്മാനങ്ങൾ നേടിയിട്ടുണ്ട്, കൂടാതെ 2019 അവസാന മൂന്ന് മാസങ്ങളിൽ 92,820 പ്രവൃത്തികൾ നടത്തി. ബോസ്റ്റണിലെ ഏറ്റവും പഴക്കമേറിയതും വലുതുമായ ദിനപത്രമാണ് ബോസ്റ്റൺ ഗ്ലോബ് .
അഫിലിയേറ്റഡ് റെസിഡൻഷ്യൽ പാർക്ക് റെസിഡന്റ്സ് അസോസിയേഷൻ: ഓസ്‌ട്രേലിയയിലെ ന്യൂ സൗത്ത് വെയിൽസിലെ പോർട്ട് മക്വാരിയിലുള്ള ഒരു രജിസ്റ്റർ ചെയ്ത ഓഫീസുമായി സംയോജിപ്പിച്ച ലാഭേച്ഛയില്ലാതെ പ്രവർത്തിക്കുന്ന ഒരു അസോസിയേഷനാണ് അഫിലിയേറ്റഡ് റെസിഡൻഷ്യൽ പാർക്ക് റെസിഡന്റ്‌സ് അസോസിയേഷൻ ഇൻ‌കോർ‌പ്പറേറ്റഡ് (ARPRA).
ദേശീയ ചെങ്‌ച്ചി സർവകലാശാല: തായ്‌വാൻ ആസ്ഥാനമായുള്ള ദേശീയ ഗവേഷണ സർവകലാശാലയാണ് നാഷണൽ ചെങ്‌ച്ചി സർവകലാശാല. റിപ്പബ്ലിക് ഓഫ് ചൈനയുടെ ആദ്യകാല പൊതു സേവന പരിശീലന കേന്ദ്രമായും ഈ സർവകലാശാല കണക്കാക്കപ്പെടുന്നു. 1927-ൽ നാൻജിംഗിൽ ആദ്യമായി സ്ഥാപിതമായ ഈ സർവകലാശാല പിന്നീട് 1954-ൽ തായ്‌പേയിലേക്ക് മാറ്റിസ്ഥാപിക്കപ്പെട്ടു. തായ്‌വാനിലെ ഏറ്റവും പ്രശസ്‌തവും പ്രമുഖവുമായ സർവകലാശാലകളിലൊന്നായി ഇത് കണക്കാക്കപ്പെടുന്നു. എൻ‌സി‌സി‌യു എന്ന് ചുരുക്കത്തിൽ അറിയപ്പെടുന്ന ഈ സർവ്വകലാശാല, കല, മാനവികത, സമൂഹമാധ്യമങ്ങൾ, ഭാഷാശാസ്ത്രം, സാഹിത്യം, സാമൂഹ്യശാസ്ത്രം, സാമ്പത്തിക ശാസ്ത്രം, മാനേജ്മെന്റ്, രാഷ്ട്രീയം, അന്താരാഷ്ട്ര കാര്യ പരിപാടികൾ എന്നിവയിൽ വൈദഗ്ദ്ധ്യം നേടി. ജേണലിസം, പരസ്യംചെയ്യൽ, റേഡിയോ, ടെലിവിഷൻ, നയതന്ത്രം, തായ്‌വാനിലെ മറ്റ് സ്ഥാപനങ്ങളിൽ പഠിപ്പിക്കാത്ത നിരവധി ഭാഷകൾ എന്നിവയിൽ കോഴ്‌സുകൾ നൽകുന്ന തായ്‌വാനിലെ പൊതു ധനസഹായമുള്ള ഏക സർവകലാശാലയാണിത്. ചെങ്‌ച്ചി (政治) എന്ന പേരിന് ഭരണം അല്ലെങ്കിൽ രാഷ്ട്രീയം എന്നാണ് അർത്ഥമാക്കുന്നത്, 1927 ൽ ചൈന റിപ്പബ്ലിക്കിലെ നാൻജിംഗ് നാഷണലിസ്റ്റ് ഗവൺമെന്റിന്റെ മുതിർന്ന സിവിൽ സർവീസിനുള്ള പരിശീലന സ്ഥാപനമായി ഇത് സ്ഥാപിക്കപ്പെട്ടു. അക്കാദമിക് സിനിക്ക, നാഷണൽ യാങ് മിംഗ് ചിയാവോ തുങ് യൂണിവേഴ്സിറ്റി, നാഷണൽ തായ്‌വാൻ യൂണിവേഴ്‌സിറ്റി, നാഷണൽ പാലസ് മ്യൂസിയം തുടങ്ങിയ അക്കാദമിക് സ്ഥാപനങ്ങളുമായി സർവകലാശാലയ്ക്ക് ശക്തമായ ബന്ധമുണ്ട്. എൻ‌സി‌സി‌യു തായ്‌വാനിലെ യൂണിവേഴ്സിറ്റി സിസ്റ്റത്തിലെ അംഗമാണ്.
നാഷണൽ കഹ്‌സിയുങ് നോർമൽ യൂണിവേഴ്സിറ്റിയിലെ സീനിയർ ഹൈസ്കൂൾ തായ്‌വാനിലെ കാവോസ്യൂങിലെ ലിംഗ്യ ജില്ലയിൽ സ്ഥിതിചെയ്യുന്ന ഒരു പൊതു ഹൈസ്‌കൂളാണ് നാഷണൽ കഹ്‌സിയുംഗ് നോർമൽ യൂണിവേഴ്‌സിറ്റിയിലെ അഫിലിയേറ്റഡ് സീനിയർ ഹൈസ്‌കൂൾ . സീനിയർ ഹൈ ലെവലിൽ ഒരു ഗ്രേഡിന് എട്ട് ക്ലാസുകളും ജൂനിയർ ഹൈ ഗ്രേഡിന് നാല് ക്ലാസുകളും പ്രാഥമിക വിദ്യാർത്ഥികൾക്ക് ഒരു ഗ്രേഡിന് ഒരു ക്ലാസും ഉണ്ട്. സ്കൂളിന്റെ കാമ്പസ് നാഷണൽ കഹ്‌സിയുങ് നോർമൽ യൂണിവേഴ്‌സിറ്റി ഉൾക്കൊള്ളുന്നു. നിലവിൽ, കഹ്‌സിയുംഗ് നഗരത്തിലെ മികച്ച ഹൈസ്കൂളുകളിൽ ഒന്നാണ് എൻ‌കെ‌എൻ‌യു‌എ‌എസ്.
നാഷണൽ തായ്‌വാൻ നോർമൽ യൂണിവേഴ്‌സിറ്റിയിലെ അഫിലിയേറ്റഡ് സീനിയർ ഹൈസ്‌കൂൾ: നാഷണൽ തായ്‌വാൻ നോർമൽ യൂണിവേഴ്‌സിറ്റിയിലെ അഫിലിയേറ്റഡ് സീനിയർ ഹൈസ്‌കൂൾ ഒരു തായ്‌വാൻ സീനിയർ ഹൈസ്‌കൂളാണ്. തായ്‌വാനിലെ എല്ലാ സീനിയർ ഹൈസ്‌കൂളുകളിലും ഇത് രണ്ടാം സ്ഥാനത്താണ്, സാധാരണയായി നാഷണൽ സീനിയർ ഹൈസ്‌കൂൾ പ്രവേശന പരീക്ഷകളിൽ PR98 ഉം അതിനുമുകളിലുള്ളവയും ആവശ്യമാണ്. തായ്‌വാനിലെ തായ്‌പേയിലെ ഡാ-ഡിസ്ട്രിക്റ്റിലാണ് കാമ്പസ് സ്ഥിതി ചെയ്യുന്നത്.
അഫിലിയേറ്റഡ് സ്റ്റേറ്റ്സ് ചാമ്പ്യൻഷിപ്പ്: ഓസ്‌ട്രേലിയൻ റഗ്ബി ലീഗ് നടത്തുന്ന വാർഷിക റഗ്ബി ലീഗ് മത്സരമാണ് അഫിലിയേറ്റഡ് സ്റ്റേറ്റ് ചാമ്പ്യൻഷിപ്പ് , നാല് അനുബന്ധ സംസ്ഥാനങ്ങളും ഓസ്‌ട്രേലിയൻ പോലീസും ഓസ്‌ട്രേലിയൻ പ്രതിരോധ സേനയും ഉൾപ്പെടുന്നു.
ദുരിതവുമായി ബന്ധപ്പെട്ടിരിക്കുന്നു: കഷ്ടത കൊണ്ട് അഫിലിയേറ്റ് നോർവീജിയൻ മരണം മെറ്റൽ ബാൻഡ്, ബ്ലഡ് റെഡ് സിംഹാസനത്തിൻറെ രണ്ടാം സ്റ്റുഡിയോ ആൽബം ആണ്. ആൽബം 2003 ജനുവരി 23 ന് പുറത്തിറങ്ങി.
സന്ദർഭോചിത പരസ്യംചെയ്യൽ: മൊബൈൽ ബ്രൗസറുകളിൽ പ്രദർശിപ്പിച്ചിരിക്കുന്ന ഉള്ളടക്കം പോലുള്ള വെബ്‌സൈറ്റുകളിലോ മറ്റ് മാധ്യമങ്ങളിലോ ദൃശ്യമാകുന്ന പരസ്യങ്ങൾക്കായുള്ള ടാർഗെറ്റുചെയ്‌ത പരസ്യത്തിന്റെ ഒരു രൂപമാണ് സന്ദർഭോചിത പരസ്യംചെയ്യൽ . സന്ദർഭ ടാർഗെറ്റിംഗിൽ, ഭാഷാ ഘടകങ്ങൾ ഉപയോഗിച്ച് ഒരു വെബ്‌സൈറ്റിന്റെ ഉള്ളടക്കത്തിന്റെ അടിസ്ഥാനത്തിലാണ് പരസ്യ മാധ്യമങ്ങളെ നിയന്ത്രിക്കുന്നത്. ഒരു ഉപയോക്താവ് നോക്കുന്നതിന്റെ സന്ദർഭത്തെ അടിസ്ഥാനമാക്കി പരസ്യങ്ങൾ സ്വയം തിരഞ്ഞെടുത്ത് ഓട്ടോമേറ്റഡ് സിസ്റ്റങ്ങൾ നൽകുന്നു.
അമേരിക്കൻ റേഡിയോ റിലേ ലീഗ്: യു‌എസ്‌എയിലെ അമേച്വർ റേഡിയോ പ്രേമികളുടെ ഏറ്റവും വലിയ അംഗത്വ അസോസിയേഷനാണ് അമേരിക്കൻ റേഡിയോ റിലേ ലീഗ് ( ARRL ). ARRL ഒരു ലാഭേച്ഛയില്ലാതെ പ്രവർത്തിക്കുന്ന ഒരു സംഘടനയാണ്, 1914 ഏപ്രിൽ 6 ന് കണക്റ്റിക്കട്ടിലെ ഹാർട്ട്ഫോർഡിലെ ഹിറാം പെർസി മാക്സിമും ക്ലാരൻസ് ഡി. തുസ്കയും ചേർന്ന് സ്ഥാപിച്ചു. ഫെഡറൽ റെഗുലേറ്ററി ബോഡികൾക്ക് മുമ്പായി അമേച്വർ റേഡിയോ ഓപ്പറേറ്റർമാരുടെ താൽപ്പര്യങ്ങളെ ARRL പ്രതിനിധീകരിക്കുന്നു, അമേച്വർ റേഡിയോ പ്രേമികൾക്ക് സാങ്കേതിക ഉപദേശവും സഹായവും നൽകുന്നു, നിരവധി വിദ്യാഭ്യാസ പരിപാടികളെ പിന്തുണയ്ക്കുന്നു, കൂടാതെ രാജ്യമെമ്പാടുമുള്ള അടിയന്തിര ആശയവിനിമയ സേവനങ്ങളെ സ്പോൺസർ ചെയ്യുന്നു. ARRL ൽ ഏകദേശം 161,000 അംഗങ്ങളുണ്ട്. യു‌എസിലെ അംഗങ്ങൾക്ക് പുറമേ, മറ്റ് രാജ്യങ്ങളിലെ 7,000 അംഗങ്ങളെ സംഘടന അവകാശപ്പെടുന്നു. ARRL നിരവധി പുസ്തകങ്ങളും പ്രതിമാസ അംഗത്വ ജേണലും QST പ്രസിദ്ധീകരിക്കുന്നു. ARRL അതിന്റെ ശതാബ്ദി കൺവെൻഷൻ 2014 ജൂലൈയിൽ കണക്റ്റിക്കട്ടിലെ ഹാർട്ട്ഫോർഡിൽ നടത്തി.
അമേരിക്കൻ റേഡിയോ റിലേ ലീഗ്: യു‌എസ്‌എയിലെ അമേച്വർ റേഡിയോ പ്രേമികളുടെ ഏറ്റവും വലിയ അംഗത്വ അസോസിയേഷനാണ് അമേരിക്കൻ റേഡിയോ റിലേ ലീഗ് ( ARRL ). ARRL ഒരു ലാഭേച്ഛയില്ലാതെ പ്രവർത്തിക്കുന്ന ഒരു സംഘടനയാണ്, 1914 ഏപ്രിൽ 6 ന് കണക്റ്റിക്കട്ടിലെ ഹാർട്ട്ഫോർഡിലെ ഹിറാം പെർസി മാക്സിമും ക്ലാരൻസ് ഡി. തുസ്കയും ചേർന്ന് സ്ഥാപിച്ചു. ഫെഡറൽ റെഗുലേറ്ററി ബോഡികൾക്ക് മുമ്പായി അമേച്വർ റേഡിയോ ഓപ്പറേറ്റർമാരുടെ താൽപ്പര്യങ്ങളെ ARRL പ്രതിനിധീകരിക്കുന്നു, അമേച്വർ റേഡിയോ പ്രേമികൾക്ക് സാങ്കേതിക ഉപദേശവും സഹായവും നൽകുന്നു, നിരവധി വിദ്യാഭ്യാസ പരിപാടികളെ പിന്തുണയ്ക്കുന്നു, കൂടാതെ രാജ്യമെമ്പാടുമുള്ള അടിയന്തിര ആശയവിനിമയ സേവനങ്ങളെ സ്പോൺസർ ചെയ്യുന്നു. ARRL ൽ ഏകദേശം 161,000 അംഗങ്ങളുണ്ട്. യു‌എസിലെ അംഗങ്ങൾക്ക് പുറമേ, മറ്റ് രാജ്യങ്ങളിലെ 7,000 അംഗങ്ങളെ സംഘടന അവകാശപ്പെടുന്നു. ARRL നിരവധി പുസ്തകങ്ങളും പ്രതിമാസ അംഗത്വ ജേണലും QST പ്രസിദ്ധീകരിക്കുന്നു. ARRL അതിന്റെ ശതാബ്ദി കൺവെൻഷൻ 2014 ജൂലൈയിൽ കണക്റ്റിക്കട്ടിലെ ഹാർട്ട്ഫോർഡിൽ നടത്തി.
അനുബന്ധ സ്കൂൾ: സ്വതന്ത്രമായി പ്രവർത്തിക്കുന്ന ഒരു വിദ്യാഭ്യാസ സ്ഥാപനമാണ് ഒരു അഫിലിയേറ്റഡ് സ്കൂൾ , മാത്രമല്ല മറ്റൊരു അക്കാദമിക് നയങ്ങൾ, മാനദണ്ഡങ്ങൾ അല്ലെങ്കിൽ പ്രോഗ്രാമുകൾ എന്നിവയിൽ നിയന്ത്രണമോ സ്വാധീനമോ ഉള്ള മറ്റൊരു വലിയ സ്ഥാപനവുമായി formal പചാരിക സഹകരണ ഉടമ്പടി ഉണ്ട്.
അനുബന്ധ സ്കൂൾ: സ്വതന്ത്രമായി പ്രവർത്തിക്കുന്ന ഒരു വിദ്യാഭ്യാസ സ്ഥാപനമാണ് ഒരു അഫിലിയേറ്റഡ് സ്കൂൾ , മാത്രമല്ല മറ്റൊരു അക്കാദമിക് നയങ്ങൾ, മാനദണ്ഡങ്ങൾ അല്ലെങ്കിൽ പ്രോഗ്രാമുകൾ എന്നിവയിൽ നിയന്ത്രണമോ സ്വാധീനമോ ഉള്ള മറ്റൊരു വലിയ സ്ഥാപനവുമായി formal പചാരിക സഹകരണ ഉടമ്പടി ഉണ്ട്.
സബ്സിഡിയറി: മറ്റൊരു കമ്പനിയുടെ ഉടമസ്ഥതയിലുള്ളതോ നിയന്ത്രിക്കുന്നതോ ആയ കമ്പനിയാണ് സബ്സിഡിയറി , സബ്സിഡിയറി കമ്പനി അല്ലെങ്കിൽ മകളുടെ കമ്പനി , ഇതിനെ മാതൃ കമ്പനി, രക്ഷകർത്താവ് അല്ലെങ്കിൽ ഹോൾഡിംഗ് കമ്പനി എന്ന് വിളിക്കുന്നു. ഒരു കമ്പനി, കോർപ്പറേഷൻ അല്ലെങ്കിൽ പരിമിതമായ ബാധ്യതാ കമ്പനി ആകാം സബ്‌സിഡിയറി. ചില സാഹചര്യങ്ങളിൽ, ഇത് സർക്കാർ അല്ലെങ്കിൽ സർക്കാർ ഉടമസ്ഥതയിലുള്ള ഒരു സംരംഭമാണ്.
കൺസോർഷ്യം: പൊതുവായ ഒരു പ്രവർത്തനത്തിൽ പങ്കെടുക്കുകയോ പൊതുവായ ലക്ഷ്യം നേടുന്നതിനായി അവരുടെ വിഭവങ്ങൾ ശേഖരിക്കുകയോ ചെയ്യുക എന്ന ലക്ഷ്യത്തോടെയുള്ള രണ്ടോ അതിലധികമോ വ്യക്തികൾ, കമ്പനികൾ, ഓർഗനൈസേഷനുകൾ അല്ലെങ്കിൽ ഗവൺമെന്റുകൾ എന്നിവയുടെ ഒരു അസോസിയേഷനാണ് കൺസോർഷ്യം .
അനുബന്ധ വിപണനം: അഫിലിയേറ്റ് മാർക്കറ്റിംഗ് എന്നത് ഒരു തരം പ്രകടന-അധിഷ്ഠിത മാർക്കറ്റിംഗാണ്, അതിൽ ഓരോ സന്ദർശകനോ ​​ഉപഭോക്താവിനോ അഫിലിയേറ്റിന്റെ സ്വന്തം മാർക്കറ്റിംഗ് പരിശ്രമങ്ങൾ വഴി ഒരു ബിസിനസ്സ് ഒന്നോ അതിലധികമോ അഫിലിയേറ്റുകൾക്ക് പ്രതിഫലം നൽകുന്നു.
അഫിലിയേറ്റഡ് ഓപ്പറേറ്റർ: ഗണിതശാസ്ത്രത്തിൽ, ഒരൊറ്റ വെക്റ്റർ സൃഷ്ടിക്കുന്ന മൊഡ്യൂളുകൾ പഠിക്കാൻ അതിരുകളില്ലാത്ത ഓപ്പറേറ്റർമാരെ ഉപയോഗിക്കുന്നതിനുള്ള ഒരു സാങ്കേതികതയായി വോൺ ന്യൂമാൻ ആൾജിബ്രാസ് സിദ്ധാന്തത്തിൽ മുറെയും വോൺ ന്യൂമാനും അഫിലിയേറ്റഡ് ഓപ്പറേറ്റർമാരെ അവതരിപ്പിച്ചു. അനന്തമായ അടിസ്ഥാന ഗ്രൂപ്പുള്ള അടച്ച മാനിഫോൾഡുകളിലെ എലിപ്റ്റിക് ഓപ്പറേറ്റർമാർക്കുള്ള സൂചിക സിദ്ധാന്തങ്ങൾ സ്വാഭാവികമായും ഗ്രൂപ്പിന്റെ വോൺ ന്യൂമാൻ ബീജഗണിതവുമായി ബന്ധപ്പെടുത്തിയിരിക്കുന്ന അതിരുകളില്ലാത്ത ഓപ്പറേറ്റർമാരെ അടിസ്ഥാനമാക്കി രൂപപ്പെടുത്താമെന്ന് പിന്നീട് അതിിയയും സിംഗറും തെളിയിച്ചു. അത്തരം സൂചിക സിദ്ധാന്തങ്ങളുടെ പഠനത്തിൽ നിന്ന് രൂപപ്പെട്ട വിശകലനത്തിനും ജ്യാമിതിക്കും ഇടയിലുള്ള ഒരു മേഖലയായ എൽ 2 കോഹമോളജിയിൽ അഫിലിയേറ്റഡ് ഓപ്പറേറ്റർമാരുടെ ബീജഗണിത സവിശേഷതകൾ പ്രധാനമാണെന്ന് തെളിഞ്ഞു.
അനുബന്ധ സ്കൂൾ: സ്വതന്ത്രമായി പ്രവർത്തിക്കുന്ന ഒരു വിദ്യാഭ്യാസ സ്ഥാപനമാണ് ഒരു അഫിലിയേറ്റഡ് സ്കൂൾ , മാത്രമല്ല മറ്റൊരു അക്കാദമിക് നയങ്ങൾ, മാനദണ്ഡങ്ങൾ അല്ലെങ്കിൽ പ്രോഗ്രാമുകൾ എന്നിവയിൽ നിയന്ത്രണമോ സ്വാധീനമോ ഉള്ള മറ്റൊരു വലിയ സ്ഥാപനവുമായി formal പചാരിക സഹകരണ ഉടമ്പടി ഉണ്ട്.
അനുബന്ധ സ്കൂൾ: സ്വതന്ത്രമായി പ്രവർത്തിക്കുന്ന ഒരു വിദ്യാഭ്യാസ സ്ഥാപനമാണ് ഒരു അഫിലിയേറ്റഡ് സ്കൂൾ , മാത്രമല്ല മറ്റൊരു അക്കാദമിക് നയങ്ങൾ, മാനദണ്ഡങ്ങൾ അല്ലെങ്കിൽ പ്രോഗ്രാമുകൾ എന്നിവയിൽ നിയന്ത്രണമോ സ്വാധീനമോ ഉള്ള മറ്റൊരു വലിയ സ്ഥാപനവുമായി formal പചാരിക സഹകരണ ഉടമ്പടി ഉണ്ട്.
നാഷണൽ കഹ്‌സിയുങ് നോർമൽ യൂണിവേഴ്സിറ്റിയിലെ സീനിയർ ഹൈസ്കൂൾ തായ്‌വാനിലെ കാവോസ്യൂങിലെ ലിംഗ്യ ജില്ലയിൽ സ്ഥിതിചെയ്യുന്ന ഒരു പൊതു ഹൈസ്‌കൂളാണ് നാഷണൽ കഹ്‌സിയുംഗ് നോർമൽ യൂണിവേഴ്‌സിറ്റിയിലെ അഫിലിയേറ്റഡ് സീനിയർ ഹൈസ്‌കൂൾ . സീനിയർ ഹൈ ലെവലിൽ ഒരു ഗ്രേഡിന് എട്ട് ക്ലാസുകളും ജൂനിയർ ഹൈ ഗ്രേഡിന് നാല് ക്ലാസുകളും പ്രാഥമിക വിദ്യാർത്ഥികൾക്ക് ഒരു ഗ്രേഡിന് ഒരു ക്ലാസും ഉണ്ട്. സ്കൂളിന്റെ കാമ്പസ് നാഷണൽ കഹ്‌സിയുങ് നോർമൽ യൂണിവേഴ്‌സിറ്റി ഉൾക്കൊള്ളുന്നു. നിലവിൽ, കഹ്‌സിയുംഗ് നഗരത്തിലെ മികച്ച ഹൈസ്കൂളുകളിൽ ഒന്നാണ് എൻ‌കെ‌എൻ‌യു‌എ‌എസ്.
നാഷണൽ തായ്‌വാൻ നോർമൽ യൂണിവേഴ്‌സിറ്റിയിലെ അഫിലിയേറ്റഡ് സീനിയർ ഹൈസ്‌കൂൾ: നാഷണൽ തായ്‌വാൻ നോർമൽ യൂണിവേഴ്‌സിറ്റിയിലെ അഫിലിയേറ്റഡ് സീനിയർ ഹൈസ്‌കൂൾ ഒരു തായ്‌വാൻ സീനിയർ ഹൈസ്‌കൂളാണ്. തായ്‌വാനിലെ എല്ലാ സീനിയർ ഹൈസ്‌കൂളുകളിലും ഇത് രണ്ടാം സ്ഥാനത്താണ്, സാധാരണയായി നാഷണൽ സീനിയർ ഹൈസ്‌കൂൾ പ്രവേശന പരീക്ഷകളിൽ PR98 ഉം അതിനുമുകളിലുള്ളവയും ആവശ്യമാണ്. തായ്‌വാനിലെ തായ്‌പേയിലെ ഡാ-ഡിസ്ട്രിക്റ്റിലാണ് കാമ്പസ് സ്ഥിതി ചെയ്യുന്നത്.
നെറ്റ്‌വർക്ക് അഫിലിയേറ്റ്: പ്രക്ഷേപണ വ്യവസായത്തിൽ, ഒരു നെറ്റ്‌വർക്ക് അഫിലിയേറ്റ് അല്ലെങ്കിൽ അഫിലിയേറ്റഡ് സ്റ്റേഷൻ എന്നത് ഒരു പ്രാദേശിക ബ്രോഡ്‌കാസ്റ്ററാണ്, ഇത് നെറ്റ്‌വർക്കിന്റെ ഉടമയല്ലാതെ മറ്റൊരു കമ്പനിയുടെ ഉടമസ്ഥതയിലുള്ളതാണ്, ഇത് ടെലിവിഷൻ പ്രോഗ്രാമുകളുടെയോ ടെലിവിഷൻ അല്ലെങ്കിൽ റേഡിയോ നെറ്റ്‌വർക്കിന്റെ റേഡിയോ പ്രോഗ്രാമുകളുടെയോ എല്ലാ അല്ലെങ്കിൽ എല്ലാ ലൈനപ്പുകളും വഹിക്കുന്നു. അത്തരമൊരു ടെലിവിഷൻ അല്ലെങ്കിൽ റേഡിയോ സ്റ്റേഷനെ രക്ഷാകർതൃ നെറ്റ്‌വർക്കിന്റെ ഉടമസ്ഥതയിലുള്ള ഒരു ഉടമസ്ഥതയിലുള്ളതും പ്രവർത്തിപ്പിക്കുന്നതുമായ സ്റ്റേഷനിൽ നിന്ന് (ഒ & ഒ) വേർതിരിക്കുന്നു.
ലേബർ പാർട്ടി (യുകെ) അനുബന്ധ ട്രേഡ് യൂണിയൻ: ബ്രിട്ടീഷ് രാഷ്ട്രീയത്തിൽ, ലേബർ പാർട്ടിയുമായി ബന്ധമുള്ള ഒരു അഫിലിയേറ്റഡ് ട്രേഡ് യൂണിയനാണ്. 1900 ൽ ട്രേഡ് യൂണിയനുകളും സോഷ്യലിസ്റ്റ് സൊസൈറ്റികളും ചേർന്നാണ് പാർട്ടി രൂപീകരിച്ചത്.
ലേബർ പാർട്ടി (യുകെ) അനുബന്ധ ട്രേഡ് യൂണിയൻ: ബ്രിട്ടീഷ് രാഷ്ട്രീയത്തിൽ, ലേബർ പാർട്ടിയുമായി ബന്ധമുള്ള ഒരു അഫിലിയേറ്റഡ് ട്രേഡ് യൂണിയനാണ്. 1900 ൽ ട്രേഡ് യൂണിയനുകളും സോഷ്യലിസ്റ്റ് സൊസൈറ്റികളും ചേർന്നാണ് പാർട്ടി രൂപീകരിച്ചത്.
കനേഡിയൻ ലേബർ കോൺഗ്രസിന്റെ അഫിലിയേറ്റഡ് യൂണിയനുകൾ: ട്രേഡ് യൂണിയനുകളുടെ ദേശീയ ഫെഡറേഷനായ കനേഡിയൻ ലേബർ കോൺഗ്രസ് ചുവടെ പട്ടികപ്പെടുത്തിയിരിക്കുന്ന സംഘടനകളാണ്:
കനേഡിയൻ ലേബർ കോൺഗ്രസിന്റെ അഫിലിയേറ്റഡ് യൂണിയനുകൾ: ട്രേഡ് യൂണിയനുകളുടെ ദേശീയ ഫെഡറേഷനായ കനേഡിയൻ ലേബർ കോൺഗ്രസ് ചുവടെ പട്ടികപ്പെടുത്തിയിരിക്കുന്ന സംഘടനകളാണ്:
ദുരിതവുമായി ബന്ധപ്പെട്ടിരിക്കുന്നു: കഷ്ടത കൊണ്ട് അഫിലിയേറ്റ് നോർവീജിയൻ മരണം മെറ്റൽ ബാൻഡ്, ബ്ലഡ് റെഡ് സിംഹാസനത്തിൻറെ രണ്ടാം സ്റ്റുഡിയോ ആൽബം ആണ്. ആൽബം 2003 ജനുവരി 23 ന് പുറത്തിറങ്ങി.
ദുരിതവുമായി ബന്ധപ്പെട്ടിരിക്കുന്നു: കഷ്ടത കൊണ്ട് അഫിലിയേറ്റ് നോർവീജിയൻ മരണം മെറ്റൽ ബാൻഡ്, ബ്ലഡ് റെഡ് സിംഹാസനത്തിൻറെ രണ്ടാം സ്റ്റുഡിയോ ആൽബം ആണ്. ആൽബം 2003 ജനുവരി 23 ന് പുറത്തിറങ്ങി.
നെറ്റ്‌വർക്ക് അഫിലിയേറ്റ്: പ്രക്ഷേപണ വ്യവസായത്തിൽ, ഒരു നെറ്റ്‌വർക്ക് അഫിലിയേറ്റ് അല്ലെങ്കിൽ അഫിലിയേറ്റഡ് സ്റ്റേഷൻ എന്നത് ഒരു പ്രാദേശിക ബ്രോഡ്‌കാസ്റ്ററാണ്, ഇത് നെറ്റ്‌വർക്കിന്റെ ഉടമയല്ലാതെ മറ്റൊരു കമ്പനിയുടെ ഉടമസ്ഥതയിലുള്ളതാണ്, ഇത് ടെലിവിഷൻ പ്രോഗ്രാമുകളുടെയോ ടെലിവിഷൻ അല്ലെങ്കിൽ റേഡിയോ നെറ്റ്‌വർക്കിന്റെ റേഡിയോ പ്രോഗ്രാമുകളുടെയോ എല്ലാ അല്ലെങ്കിൽ എല്ലാ ലൈനപ്പുകളും വഹിക്കുന്നു. അത്തരമൊരു ടെലിവിഷൻ അല്ലെങ്കിൽ റേഡിയോ സ്റ്റേഷനെ രക്ഷാകർതൃ നെറ്റ്‌വർക്കിന്റെ ഉടമസ്ഥതയിലുള്ള ഒരു ഉടമസ്ഥതയിലുള്ളതും പ്രവർത്തിപ്പിക്കുന്നതുമായ സ്റ്റേഷനിൽ നിന്ന് (ഒ & ഒ) വേർതിരിക്കുന്നു.
ട്രേഡ്സ് യൂണിയൻ കോൺഗ്രസിന്റെ അനുബന്ധ സ്ഥാപനങ്ങളുടെ പട്ടിക: ഇത് ട്രേഡ്സ് യൂണിയൻ കോൺഗ്രസിന്റെ അഫിലിയേറ്റുകളുടെ ഒരു പട്ടികയാണ്, അതായത് ട്രേഡ്സ് യൂണിയൻ കോൺഗ്രസിന്റെ അംഗ ട്രേഡ് യൂണിയനുകൾ.
ലിബറേഷൻ ടൈഗേഴ്‌സ് ഓഫ് തമിഴ് ഈലവുമായി ബന്ധപ്പെട്ടവ: മുമ്പ് വടക്കൻ ശ്രീലങ്ക ആസ്ഥാനമായിരുന്ന വിഘടനവാദി തീവ്രവാദ സംഘടനയായ ലിബറേഷൻ ടൈഗേഴ്സ് ഓഫ് തമിഴ് ഈലം (എൽടിടിഇ) ഇതിനോട് അനുബന്ധിച്ച് വിവിധ സംഘടനകൾ ഉണ്ടായിരുന്നു. ചാരിറ്റബിൾ ഓർഗനൈസേഷനുകൾ, രാഷ്ട്രീയ പാർട്ടികൾ, സംസ്ഥാന രഹസ്യാന്വേഷണ സംഘടനകൾ, ശ്രീലങ്കയിലെയും മറ്റ് രാജ്യങ്ങളിലെയും സർക്കാരുകൾ എന്നിവ ഇതിൽ ഉൾപ്പെടുന്നു. 2009 ൽ പുലികൾ സൈനികപരമായി പരാജയപ്പെട്ടുവെങ്കിലും നിരവധി വിദേശ അധിഷ്ഠിത സംഘടനകൾ ഇപ്പോഴും അതിന്റെ പ്രത്യയശാസ്ത്രത്തെ പ്രോത്സാഹിപ്പിക്കുകയാണെന്ന് ശ്രീലങ്കൻ സർക്കാർ ആരോപിക്കുന്നു.
കൊളീജിയറ്റ് സർവകലാശാല: ഒരു കേന്ദ്ര ഭരണകൂടവും നിരവധി ഘടക കോളേജുകളും തമ്മിൽ വിഭജിച്ചിരിക്കുന്ന ഒരു സർവ്വകലാശാലയാണ് ഒരു കൊളീജിയറ്റ് സർവകലാശാല . ചരിത്രപരമായി, ആദ്യത്തെ കൊളീജിയറ്റ് സർവകലാശാല പാരീസ് സർവകലാശാലയും അതിന്റെ ആദ്യത്തെ കോളേജ് കൊളാഷ് ഡെസ് ഡിക്സ്-ഹ്യൂട്ടും ആയിരുന്നു. രണ്ട് പ്രധാന രൂപങ്ങൾ റെസിഡൻഷ്യൽ കോളേജ് സർവ്വകലാശാലകളാണ്, അവിടെ കേന്ദ്ര സർവകലാശാലയ്ക്ക് അദ്ധ്യാപനത്തിന്റെ ഉത്തരവാദിത്തമുണ്ട്, കോളേജുകൾക്ക് ചില അദ്ധ്യാപനങ്ങൾ നൽകാം, പക്ഷേ പ്രാഥമികമായി റെസിഡൻഷ്യൽ കമ്മ്യൂണിറ്റികളാണ്, കൂടാതെ കേന്ദ്ര സർവകലാശാലകൾക്ക് ഭരണപരമായ പങ്കുള്ള കോളേജുകൾ റെസിഡൻഷ്യൽ ആയിരിക്കാമെങ്കിലും പ്രാഥമികമായി പഠിപ്പിക്കുന്ന ഫെഡറൽ സർവകലാശാലകൾ സ്ഥാപനങ്ങൾ. ഫെഡറൽ കോളജുകളുടെ വലിയ കോളേജുകൾ അല്ലെങ്കിൽ കാമ്പസുകൾ, യൂണിവേഴ്സിറ്റി കോളേജ് ലണ്ടൻ, കാലിഫോർണിയ യൂണിവേഴ്സിറ്റി, ബെർക്ക്‌ലി എന്നിവ ഫലപ്രദമായി സ്വന്തം സർവ്വകലാശാലകളായിരിക്കാം, പലപ്പോഴും അവർക്ക് സ്വന്തമായി വിദ്യാർത്ഥി യൂണിയനുകളുണ്ടാകാം.
കൊളീജിയറ്റ് സർവകലാശാല: ഒരു കേന്ദ്ര ഭരണകൂടവും നിരവധി ഘടക കോളേജുകളും തമ്മിൽ വിഭജിച്ചിരിക്കുന്ന ഒരു സർവ്വകലാശാലയാണ് ഒരു കൊളീജിയറ്റ് സർവകലാശാല . ചരിത്രപരമായി, ആദ്യത്തെ കൊളീജിയറ്റ് സർവകലാശാല പാരീസ് സർവകലാശാലയും അതിന്റെ ആദ്യത്തെ കോളേജ് കൊളാഷ് ഡെസ് ഡിക്സ്-ഹ്യൂട്ടും ആയിരുന്നു. രണ്ട് പ്രധാന രൂപങ്ങൾ റെസിഡൻഷ്യൽ കോളേജ് സർവ്വകലാശാലകളാണ്, അവിടെ കേന്ദ്ര സർവകലാശാലയ്ക്ക് അദ്ധ്യാപനത്തിന്റെ ഉത്തരവാദിത്തമുണ്ട്, കോളേജുകൾക്ക് ചില അദ്ധ്യാപനങ്ങൾ നൽകാം, പക്ഷേ പ്രാഥമികമായി റെസിഡൻഷ്യൽ കമ്മ്യൂണിറ്റികളാണ്, കൂടാതെ കേന്ദ്ര സർവകലാശാലകൾക്ക് ഭരണപരമായ പങ്കുള്ള കോളേജുകൾ റെസിഡൻഷ്യൽ ആയിരിക്കാമെങ്കിലും പ്രാഥമികമായി പഠിപ്പിക്കുന്ന ഫെഡറൽ സർവകലാശാലകൾ സ്ഥാപനങ്ങൾ. ഫെഡറൽ കോളജുകളുടെ വലിയ കോളേജുകൾ അല്ലെങ്കിൽ കാമ്പസുകൾ, യൂണിവേഴ്സിറ്റി കോളേജ് ലണ്ടൻ, കാലിഫോർണിയ യൂണിവേഴ്സിറ്റി, ബെർക്ക്‌ലി എന്നിവ ഫലപ്രദമായി സ്വന്തം സർവ്വകലാശാലകളായിരിക്കാം, പലപ്പോഴും അവർക്ക് സ്വന്തമായി വിദ്യാർത്ഥി യൂണിയനുകളുണ്ടാകാം.
കൊളീജിയറ്റ് സർവകലാശാല: ഒരു കേന്ദ്ര ഭരണകൂടവും നിരവധി ഘടക കോളേജുകളും തമ്മിൽ വിഭജിച്ചിരിക്കുന്ന ഒരു സർവ്വകലാശാലയാണ് ഒരു കൊളീജിയറ്റ് സർവകലാശാല . ചരിത്രപരമായി, ആദ്യത്തെ കൊളീജിയറ്റ് സർവകലാശാല പാരീസ് സർവകലാശാലയും അതിന്റെ ആദ്യത്തെ കോളേജ് കൊളാഷ് ഡെസ് ഡിക്സ്-ഹ്യൂട്ടും ആയിരുന്നു. രണ്ട് പ്രധാന രൂപങ്ങൾ റെസിഡൻഷ്യൽ കോളേജ് സർവ്വകലാശാലകളാണ്, അവിടെ കേന്ദ്ര സർവകലാശാലയ്ക്ക് അദ്ധ്യാപനത്തിന്റെ ഉത്തരവാദിത്തമുണ്ട്, കോളേജുകൾക്ക് ചില അദ്ധ്യാപനങ്ങൾ നൽകാം, പക്ഷേ പ്രാഥമികമായി റെസിഡൻഷ്യൽ കമ്മ്യൂണിറ്റികളാണ്, കൂടാതെ കേന്ദ്ര സർവകലാശാലകൾക്ക് ഭരണപരമായ പങ്കുള്ള കോളേജുകൾ റെസിഡൻഷ്യൽ ആയിരിക്കാമെങ്കിലും പ്രാഥമികമായി പഠിപ്പിക്കുന്ന ഫെഡറൽ സർവകലാശാലകൾ സ്ഥാപനങ്ങൾ. ഫെഡറൽ കോളജുകളുടെ വലിയ കോളേജുകൾ അല്ലെങ്കിൽ കാമ്പസുകൾ, യൂണിവേഴ്സിറ്റി കോളേജ് ലണ്ടൻ, കാലിഫോർണിയ യൂണിവേഴ്സിറ്റി, ബെർക്ക്‌ലി എന്നിവ ഫലപ്രദമായി സ്വന്തം സർവ്വകലാശാലകളായിരിക്കാം, പലപ്പോഴും അവർക്ക് സ്വന്തമായി വിദ്യാർത്ഥി യൂണിയനുകളുണ്ടാകാം.
ബന്ധം: അഫിലിയേഷൻ അല്ലെങ്കിൽ അഫിലിയേറ്റ് ഇനിപ്പറയുന്നവയെ പരാമർശിക്കാം: അഫിലിയേറ്റ് (കൊമേഴ്‌സ്), ബിസിനസ് നിയമത്തിൽ ഉപയോഗിക്കുന്ന എന്റിറ്റി ബന്ധത്തിന്റെ നിയമപരമായ രൂപം അഫിലിയേഷൻ, കുടുംബ ബന്ധത്തിന്റെ നിയമപരമായ രൂപം അനുബന്ധ വിപണനം അഫിലിയേറ്റ് നെറ്റ്‌വർക്ക് അല്ലെങ്കിൽ അഫിലിയേഷൻ പ്ലാറ്റ്ഫോം, പരസ്യദാതാക്കളെയും അഫിലിയേറ്റുകളെയും ബന്ധിപ്പിക്കുന്ന ഒരു വെബ്‌സൈറ്റ് അഫിലിയേറ്റഡ് ട്രേഡ് യൂണിയൻ, ബ്രിട്ടീഷ് രാഷ്ട്രീയത്തിൽ, ബ്രിട്ടീഷ് ലേബർ പാർട്ടിയുമായി ബന്ധമുള്ള ഒരു ട്രേഡ് യൂണിയൻ നെറ്റ്‌വർക്ക് അഫിലിയേറ്റ്, പ്രക്ഷേപണ കമ്പനികൾ തമ്മിലുള്ള ബന്ധം അഫിലിയേഷന്റെ ആവശ്യകത, ഒരു വ്യക്തിയുടെ പങ്കാളിത്തം അനുഭവപ്പെടേണ്ടതും ഒരു സാമൂഹിക ഗ്രൂപ്പിനുള്ളിൽ "ഉൾപ്പെടുന്നതും" രാഷ്ട്രീയ പാർട്ടി അഫിലിയേഷൻ മതപരമായ ബന്ധം സാമൂഹിക അഫിലിയേഷൻ അഫിലിയേറ്റഡ് ട്രേഡ് യൂണിയൻ അനുബന്ധ സ്കൂൾ അഫിലിയേറ്റഡ് ഓപ്പറേറ്റർ, ഗണിതത്തിൽ ഒരു കൺസോർഷ്യം അല്ലെങ്കിൽ ട്രേഡ് അസോസിയേഷന് സമാനമായ അനുബന്ധ സ്ഥാപനം ക്യൂബെക്കിലെ രജിസ്റ്റർ ചെയ്ത രാഷ്ട്രീയ പാർട്ടിയാണ് അഫിലിയേഷൻ ക്യൂബെക്ക് അനുബന്ധ സർവകലാശാല അഫിലിയേറ്റഡ് (ആൽബം) , എംസി ഐഹറ്റിന്റെ 2006 റാപ്പ് ആൽബം
അഫിലിയേഷൻ ക്യൂബെക്ക്: 2008 മുതൽ 2012 വരെ കാനഡയിലെ ക്യൂബെക്കിൽ രജിസ്റ്റർ ചെയ്ത ഒരു രാഷ്ട്രീയ പാർട്ടിയായിരുന്നു അഫിലിയേഷൻ ക്യൂബെക്ക്. ഇത് കനേഡിയൻ ഐക്യത്തിന് അനുകൂലമായിരുന്നു, ക്യൂബെക്ക് ദേശീയതയെയും പരമാധികാരത്തെയും എതിർത്തു. പാർട്ടിയുടെ ഫെഡറലിസ്റ്റ് അജണ്ട മാറ്റിനിർത്തിയാൽ, "ക്യൂബെക്ക് പ്രവിശ്യയിൽ താമസിക്കുന്ന കനേഡിയൻമാരുടെ മുഴുവൻ അവകാശങ്ങളും താൽപ്പര്യങ്ങളും സജീവമായി പിന്തുടരുക" എന്നതായിരുന്നു അതിന്റെ പ്രഖ്യാപിത ദ mission ത്യം. ക്യൂബെക്കിന്റെ ഭാഷാ നിയമത്തെയും ഇത് എതിർത്തു. പാർട്ടി ഒരു തിരഞ്ഞെടുപ്പിലും മത്സരിച്ചിട്ടില്ല. അതിന്റെ സഹസ്ഥാപകനും നേതാവുമായ അലൻ ഇ. നൂട്ടിക് പദ്ധതിയിൽ നിന്ന് രാജിവച്ചതിനെത്തുടർന്ന് പാർട്ടി പ്രവർത്തനരഹിതമാവുകയും 2012 ജനുവരി 30 ന് രജിസ്റ്റർ ചെയ്ത പാർട്ടിയുടെ പദവി നഷ്ടപ്പെടുകയും ചെയ്തു.
ബന്ധം: അഫിലിയേഷൻ അല്ലെങ്കിൽ അഫിലിയേറ്റ് ഇനിപ്പറയുന്നവയെ പരാമർശിക്കാം: അഫിലിയേറ്റ് (കൊമേഴ്‌സ്), ബിസിനസ് നിയമത്തിൽ ഉപയോഗിക്കുന്ന എന്റിറ്റി ബന്ധത്തിന്റെ നിയമപരമായ രൂപം അഫിലിയേഷൻ, കുടുംബ ബന്ധത്തിന്റെ നിയമപരമായ രൂപം അനുബന്ധ വിപണനം അഫിലിയേറ്റ് നെറ്റ്‌വർക്ക് അല്ലെങ്കിൽ അഫിലിയേഷൻ പ്ലാറ്റ്ഫോം, പരസ്യദാതാക്കളെയും അഫിലിയേറ്റുകളെയും ബന്ധിപ്പിക്കുന്ന ഒരു വെബ്‌സൈറ്റ് അഫിലിയേറ്റഡ് ട്രേഡ് യൂണിയൻ, ബ്രിട്ടീഷ് രാഷ്ട്രീയത്തിൽ, ബ്രിട്ടീഷ് ലേബർ പാർട്ടിയുമായി ബന്ധമുള്ള ഒരു ട്രേഡ് യൂണിയൻ നെറ്റ്‌വർക്ക് അഫിലിയേറ്റ്, പ്രക്ഷേപണ കമ്പനികൾ തമ്മിലുള്ള ബന്ധം അഫിലിയേഷന്റെ ആവശ്യകത, ഒരു വ്യക്തിയുടെ പങ്കാളിത്തം അനുഭവപ്പെടേണ്ടതും ഒരു സാമൂഹിക ഗ്രൂപ്പിനുള്ളിൽ "ഉൾപ്പെടുന്നതും" രാഷ്ട്രീയ പാർട്ടി അഫിലിയേഷൻ മതപരമായ ബന്ധം സാമൂഹിക അഫിലിയേഷൻ അഫിലിയേറ്റഡ് ട്രേഡ് യൂണിയൻ അനുബന്ധ സ്കൂൾ അഫിലിയേറ്റഡ് ഓപ്പറേറ്റർ, ഗണിതത്തിൽ ഒരു കൺസോർഷ്യം അല്ലെങ്കിൽ ട്രേഡ് അസോസിയേഷന് സമാനമായ അനുബന്ധ സ്ഥാപനം ക്യൂബെക്കിലെ രജിസ്റ്റർ ചെയ്ത രാഷ്ട്രീയ പാർട്ടിയാണ് അഫിലിയേഷൻ ക്യൂബെക്ക് അനുബന്ധ സർവകലാശാല അഫിലിയേറ്റഡ് (ആൽബം) , എംസി ഐഹറ്റിന്റെ 2006 റാപ്പ് ആൽബം
അഫിലിയേഷൻ (കുടുംബ നിയമം): നിയമത്തിൽ, പിതൃത്വം നിയമപരമായി സ്ഥാപിക്കുന്നതിനെ വിവരിക്കുന്നതിന് മുമ്പ് അഫിലിയേഷൻ എന്ന പദമായിരുന്നു. ഇനിപ്പറയുന്ന വിവരണം മിക്കവാറും 20-ആം നൂറ്റാണ്ടിന്റെ തുടക്കത്തിൽ എഴുതിയതാണ്, ഇത് ഒരു ചരിത്ര രേഖയായി മനസ്സിലാക്കണം.
അഫിലിയേഷൻ ക്യൂബെക്ക്: 2008 മുതൽ 2012 വരെ കാനഡയിലെ ക്യൂബെക്കിൽ രജിസ്റ്റർ ചെയ്ത ഒരു രാഷ്ട്രീയ പാർട്ടിയായിരുന്നു അഫിലിയേഷൻ ക്യൂബെക്ക്. ഇത് കനേഡിയൻ ഐക്യത്തിന് അനുകൂലമായിരുന്നു, ക്യൂബെക്ക് ദേശീയതയെയും പരമാധികാരത്തെയും എതിർത്തു. പാർട്ടിയുടെ ഫെഡറലിസ്റ്റ് അജണ്ട മാറ്റിനിർത്തിയാൽ, "ക്യൂബെക്ക് പ്രവിശ്യയിൽ താമസിക്കുന്ന കനേഡിയൻമാരുടെ മുഴുവൻ അവകാശങ്ങളും താൽപ്പര്യങ്ങളും സജീവമായി പിന്തുടരുക" എന്നതായിരുന്നു അതിന്റെ പ്രഖ്യാപിത ദ mission ത്യം. ക്യൂബെക്കിന്റെ ഭാഷാ നിയമത്തെയും ഇത് എതിർത്തു. പാർട്ടി ഒരു തിരഞ്ഞെടുപ്പിലും മത്സരിച്ചിട്ടില്ല. അതിന്റെ സഹസ്ഥാപകനും നേതാവുമായ അലൻ ഇ. നൂട്ടിക് പദ്ധതിയിൽ നിന്ന് രാജിവച്ചതിനെത്തുടർന്ന് പാർട്ടി പ്രവർത്തനരഹിതമാവുകയും 2012 ജനുവരി 30 ന് രജിസ്റ്റർ ചെയ്ത പാർട്ടിയുടെ പദവി നഷ്ടപ്പെടുകയും ചെയ്തു.
അനുബന്ധ സംഘട്ടന സിദ്ധാന്തം: പരസ്പരവിനിമയം ഉൾക്കൊള്ളുന്ന ഒരു സാമൂഹിക മന psych ശാസ്ത്രപരമായ സമീപനമാണ് അഫിലിയേറ്റീവ് സംഘട്ടന സിദ്ധാന്തം ( ACT ). ഈ സിദ്ധാന്തം "ആളുകൾക്ക് അടുപ്പത്തിനും സ്വയംഭരണത്തിനുമായി മത്സര ആവശ്യങ്ങളോ ആഗ്രഹങ്ങളോ ഉണ്ട്" എന്ന് വാദിക്കുന്നു. ഏതൊരു ബന്ധത്തിലും, ആളുകൾ‌ക്ക് ചർച്ചകൾ‌ നടത്തുകയും അവർ‌ എന്തിനാണ് പെരുമാറുന്നതെന്ന് യുക്തിസഹമായി മനസ്സിലാക്കാൻ‌ ശ്രമിക്കുകയും ചെയ്യും.
അനുബന്ധ സംഘട്ടന സിദ്ധാന്തം: പരസ്പരവിനിമയം ഉൾക്കൊള്ളുന്ന ഒരു സാമൂഹിക മന psych ശാസ്ത്രപരമായ സമീപനമാണ് അഫിലിയേറ്റീവ് സംഘട്ടന സിദ്ധാന്തം ( ACT ). ഈ സിദ്ധാന്തം "ആളുകൾക്ക് അടുപ്പത്തിനും സ്വയംഭരണത്തിനുമായി മത്സര ആവശ്യങ്ങളോ ആഗ്രഹങ്ങളോ ഉണ്ട്" എന്ന് വാദിക്കുന്നു. ഏതൊരു ബന്ധത്തിലും, ആളുകൾ‌ക്ക് ചർച്ചകൾ‌ നടത്തുകയും അവർ‌ എന്തിനാണ് പെരുമാറുന്നതെന്ന് യുക്തിസഹമായി മനസ്സിലാക്കാൻ‌ ശ്രമിക്കുകയും ചെയ്യും.
ബെംഗ്ബു മെഡിക്കൽ കോളേജ്: പീപ്പിൾസ് റിപ്പബ്ലിക്ക് ഓഫ് ചൈനയിലെ അൻഹുയി പ്രവിശ്യയിലെ ബെംഗ്ബുവിലുള്ള ദേശീയ മെഡിക്കൽ കോളേജാണ് ബെംഗ്ബു മെഡിക്കൽ കോളേജ് , അൻഹുയി പ്രവിശ്യയിലെ വിദ്യാഭ്യാസ ബ്യൂറോയുടെ അധികാരപരിധിയിൽ നേരിട്ട് മേൽനോട്ടം വഹിക്കുന്നു.
അഫിലിൻ: ആന്റിജനുകൾ തിരഞ്ഞെടുത്ത് ബന്ധിപ്പിക്കാൻ രൂപകൽപ്പന ചെയ്ത കൃത്രിമ പ്രോട്ടീനുകളാണ് അഫിലിനുകൾ . അഫിലിൻ പ്രോട്ടീനുകൾ ഘടനാപരമായി മനുഷ്യ ubiquitin ൽ നിന്ന് ഉരുത്തിരിഞ്ഞതാണ്. ഈ പ്രോട്ടീനുകളുടെ ഉപരിതലത്തിൽ ദൃശ്യമാകുന്ന അമിനോ ആസിഡുകൾ പരിഷ്കരിച്ചാണ് അഫിലിൻ പ്രോട്ടീനുകൾ നിർമ്മിക്കുന്നത്, കൂടാതെ ഫെയ്ജ് ഡിസ്പ്ലേ, സ്ക്രീനിംഗ് പോലുള്ള ഡിസ്പ്ലേ ടെക്നിക്കുകൾ ഉപയോഗിച്ച് വേർതിരിച്ചിരിക്കുന്നു. അവ ആന്റിബോഡികളോട് സാമ്യമുള്ളതും ആന്റിജനുകളോടുള്ള പ്രത്യേകതയുമാണ്, പക്ഷേ ഘടനയിലല്ല, ഇത് അവയെ ഒരു തരം ആന്റിബോഡി മൈമെറ്റിക് ആക്കുന്നു. പുതിയ ബയോഫാർമസ്യൂട്ടിക്കൽ മരുന്നുകൾ, ഡയഗ്നോസ്റ്റിക്സ്, അഫിനിറ്റി ലിഗാൻഡുകൾ എന്നിവയായി അഫിലിൻ വികസിപ്പിച്ചെടുത്തത് സ്കിൽ പ്രോട്ടീൻ ജിഎംബിഎച്ച് ആണ്.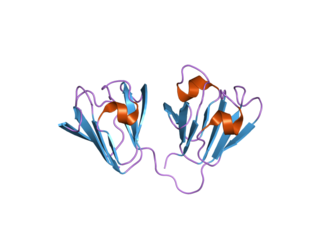
അഫിലിയേറ്റഡ്: അഫ്ഫിലിയതെദ് ദൊഒമ്ത്രെഎ പ്രകാരം, ഗയ്ന്ഗ്സ് '2010 അരങ്ങേറ്റം സ്റ്റുഡിയോ ആൽബം, രെലയ്തെദ് ഒരു റീമിക്സ് ഇ.പി. ആണ്. ഇത് 2011 മാർച്ച് 4 ന് സ്റ്റീരിയോഗത്തിൽ പ്രദർശിപ്പിച്ചു. സെസിൽ ഒട്ടർ, പേപ്പർ ടൈഗർ, പി‌ഒ‌എസ്, ലാസർ‌ബീക്ക് എന്നിവരാണ് ഇപി നിർമ്മിച്ചത്. അവയിൽ‌ നിന്നും ഒരു പുതിയ ഗാനം നിർമ്മിക്കുന്നതിന് നിർമ്മാതാക്കൾ‌ക്ക് റിലേറ്റഡ് 10 റാൻഡം കാണ്ഡം കൈമാറി. 2011 മാർച്ച് 6 ന് ഫസ്റ്റ് അവന്യൂവിലാണ് ഇപിയുടെ റിലീസ് ഷോ നടന്നത്.
നെറ്റ്‌വർക്ക് അഫിലിയേറ്റ്: പ്രക്ഷേപണ വ്യവസായത്തിൽ, ഒരു നെറ്റ്‌വർക്ക് അഫിലിയേറ്റ് അല്ലെങ്കിൽ അഫിലിയേറ്റഡ് സ്റ്റേഷൻ എന്നത് ഒരു പ്രാദേശിക ബ്രോഡ്‌കാസ്റ്ററാണ്, ഇത് നെറ്റ്‌വർക്കിന്റെ ഉടമയല്ലാതെ മറ്റൊരു കമ്പനിയുടെ ഉടമസ്ഥതയിലുള്ളതാണ്, ഇത് ടെലിവിഷൻ പ്രോഗ്രാമുകളുടെയോ ടെലിവിഷൻ അല്ലെങ്കിൽ റേഡിയോ നെറ്റ്‌വർക്കിന്റെ റേഡിയോ പ്രോഗ്രാമുകളുടെയോ എല്ലാ അല്ലെങ്കിൽ എല്ലാ ലൈനപ്പുകളും വഹിക്കുന്നു. അത്തരമൊരു ടെലിവിഷൻ അല്ലെങ്കിൽ റേഡിയോ സ്റ്റേഷനെ രക്ഷാകർതൃ നെറ്റ്‌വർക്കിന്റെ ഉടമസ്ഥതയിലുള്ള ഒരു ഉടമസ്ഥതയിലുള്ളതും പ്രവർത്തിപ്പിക്കുന്നതുമായ സ്റ്റേഷനിൽ നിന്ന് (ഒ & ഒ) വേർതിരിക്കുന്നു.
സ്ഥിരീകരിക്കുന്നയാൾ: ആന്റിബോഡികളുമായി സമാനമായ സവിശേഷതയോടും അടുപ്പത്തോടും കൂടിയ തന്മാത്രകളെ ബന്ധിപ്പിക്കുന്ന ചെറിയ പ്രോട്ടീനുകളാണ് അഫിമർ തന്മാത്രകൾ . വിവിധ ആപ്ലിക്കേഷനുകളിലെ മോണോക്ലോണൽ ആന്റിബോഡികളുടെ തന്മാത്രാ തിരിച്ചറിയൽ സവിശേഷതകളെ അനുകരിക്കുന്നതിനാണ് ഈ എഞ്ചിനീയറിംഗ് ആന്റിബോഡി ബൈൻഡിംഗ് പ്രോട്ടീനുകൾ രൂപകൽപ്പന ചെയ്തിരിക്കുന്നത്. കൂടാതെ, ഈ അഫിനിറ്റി റിയാജന്റുകൾ അവയുടെ സ്ഥിരത വർദ്ധിപ്പിക്കുന്നതിനും താപനിലയെയും പിഎച്ചിനെയും സഹിഷ്ണുത പുലർത്തുന്നതിനും അവയുടെ വലുപ്പം കുറയ്ക്കുന്നതിനും ഇ.കോളി , സസ്തന കോശങ്ങളിൽ അവയുടെ ആവിഷ്കാരം വർദ്ധിപ്പിക്കുന്നതിനും ഒപ്റ്റിമൈസ് ചെയ്തിട്ടുണ്ട്.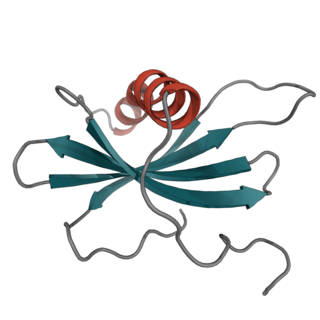
സ്ഥിരീകരിക്കുന്നയാൾ: ആന്റിബോഡികളുമായി സമാനമായ സവിശേഷതയോടും അടുപ്പത്തോടും കൂടിയ തന്മാത്രകളെ ബന്ധിപ്പിക്കുന്ന ചെറിയ പ്രോട്ടീനുകളാണ് അഫിമർ തന്മാത്രകൾ . വിവിധ ആപ്ലിക്കേഷനുകളിലെ മോണോക്ലോണൽ ആന്റിബോഡികളുടെ തന്മാത്രാ തിരിച്ചറിയൽ സവിശേഷതകളെ അനുകരിക്കുന്നതിനാണ് ഈ എഞ്ചിനീയറിംഗ് ആന്റിബോഡി ബൈൻഡിംഗ് പ്രോട്ടീനുകൾ രൂപകൽപ്പന ചെയ്തിരിക്കുന്നത്. കൂടാതെ, ഈ അഫിനിറ്റി റിയാജന്റുകൾ അവയുടെ സ്ഥിരത വർദ്ധിപ്പിക്കുന്നതിനും താപനിലയെയും പിഎച്ചിനെയും സഹിഷ്ണുത പുലർത്തുന്നതിനും അവയുടെ വലുപ്പം കുറയ്ക്കുന്നതിനും ഇ.കോളി , സസ്തന കോശങ്ങളിൽ അവയുടെ ആവിഷ്കാരം വർദ്ധിപ്പിക്കുന്നതിനും ഒപ്റ്റിമൈസ് ചെയ്തിട്ടുണ്ട്.
സ്പീഷിസ് അഫിനിസ്: സുവോളജിയിലും സസ്യശാസ്ത്രത്തിലും ടാക്സോണമിക് ടെർമിനോളജിയാണ് സ്പീഷിസ് അഫിനിസ് . ഓപ്പൺ നാമകരണത്തിൽ, ലഭ്യമായ വസ്തുക്കളോ തെളിവുകളോ നിർദ്ദേശിക്കുന്നത് നിർദ്ദിഷ്ട ഇനങ്ങളുമായി ബന്ധപ്പെട്ടതാണെന്നും അവയുമായി ഒരു ബന്ധമുണ്ടെന്നും എന്നാൽ അതിന് സമാനമല്ലെന്നും, അതിനുശേഷം വരുന്ന ദ്വിപദ നാമമുള്ള സ്പീഷിസുകളാണ്. ലാറ്റിൻ പദമായ അഫിനിസ് "ഇതുമായി ബന്ധപ്പെട്ടിരിക്കുന്നു" അല്ലെങ്കിൽ "സമാനമാണ്" എന്ന് വിവർത്തനം ചെയ്യാം.
അഫിൻ ബാങ്ക്: ഏല്യാമ ബെര്ഹദ് DBA ഏല്യാമ ഏല്യാമ ഇസ്ലാമിക് ബാങ്ക് ബെര്ഹദ്, ഏല്യാമ ഹുവാംഗ് ഇൻവെസ്റ്റ്മെന്റ് ബാങ്ക് ബെര്ഹദ്, ഏല്യാമ മൊനെയ്ബ്രൊകെര്സ് സ്ദ്ന് ജാന് ആൻഡ് അക്സഅ ഏല്യാമ ലൈഫ് ഇൻഷുറൻസ് ബെര്ഹദ് സാമ്പത്തിക ഹോൾഡിങ് കമ്പനിയാണ്. അഫിൻ ബാങ്ക് ബെർഹാദിന്റെ ഒരു അസോസിയേറ്റ് കമ്പനിയാണ് ആക്‌സ അഫിൻ ജനറൽ ഇൻഷുറൻസ് ബെർഹാദ്.
അഫിൻ ബാങ്ക്: ഏല്യാമ ബെര്ഹദ് DBA ഏല്യാമ ഏല്യാമ ഇസ്ലാമിക് ബാങ്ക് ബെര്ഹദ്, ഏല്യാമ ഹുവാംഗ് ഇൻവെസ്റ്റ്മെന്റ് ബാങ്ക് ബെര്ഹദ്, ഏല്യാമ മൊനെയ്ബ്രൊകെര്സ് സ്ദ്ന് ജാന് ആൻഡ് അക്സഅ ഏല്യാമ ലൈഫ് ഇൻഷുറൻസ് ബെര്ഹദ് സാമ്പത്തിക ഹോൾഡിങ് കമ്പനിയാണ്. അഫിൻ ബാങ്ക് ബെർഹാദിന്റെ ഒരു അസോസിയേറ്റ് കമ്പനിയാണ് ആക്‌സ അഫിൻ ജനറൽ ഇൻഷുറൻസ് ബെർഹാദ്.
അഫിൻ ഹ്വാംഗ് ക്യാപിറ്റൽ: മലേഷ്യൻ ആസ്ഥാനമായുള്ള ഇൻവെസ്റ്റ്‌മെന്റ് ബാങ്കിംഗ് ഗ്രൂപ്പായ അഫിൻ ഹ്വാംഗ് ഇൻവെസ്റ്റ്‌മെന്റ് ബാങ്ക് ബെർഹാദിന്റെ ബ്രാൻഡ് നാമമാണ് അഫിൻ ഹ്വാംഗ് ക്യാപിറ്റൽ , 2014 സെപ്റ്റംബറിൽ രൂപീകരിച്ചു.
അഫൈൻ കോമ്പിനേഷൻ: ഗണിതശാസ്ത്രം, X 1 ഒരു അഫ്ഫിനെ സംയുക്തമായും, ..., x n ഒരു ലീനിയർ സംയോജനമാണ്
ചീസ് വിളഞ്ഞത്: ചീസ് പാകമാകൽ , പകരമായി ചീസ് നീളുന്നു അല്ലെങ്കിൽ അഫിനേജ് , ചീസ് നിർമ്മാണത്തിലെ ഒരു പ്രക്രിയയാണ്. ചീസിലെ വ്യത്യസ്തമായ സ്വാദിന് ഇത് ഉത്തരവാദിയാണ്, കൂടാതെ " പാകമാകുന്ന ഏജന്റുമാരുടെ " പരിഷ്‌ക്കരണത്തിലൂടെ, രുചി, ഘടന, ശരീരം എന്നിങ്ങനെയുള്ള പലതരം പാൽക്കട്ടകളെ നിർവചിക്കുന്ന സവിശേഷതകൾ നിർണ്ണയിക്കുന്നു. "പാലിന്റെ ബാക്ടീരിയ, എൻസൈമുകൾ, ലാക്റ്റിക് സംസ്കാരം, റെനെറ്റ്, ലിപെയ്സുകൾ, ചേർത്ത അച്ചുകൾ അല്ലെങ്കിൽ യീസ്റ്റുകൾ, പാരിസ്ഥിതിക മലിനീകരണം" എന്നിവയുടെ ഏജന്റുമാരെ ഉൾക്കൊള്ളുന്ന സങ്കീർണ്ണമായ ശാരീരിക, രാസ, മൈക്രോബയോളജിക്കൽ മാറ്റങ്ങളുടെ ഒരു പരമ്പരയാണ് ഈ പ്രക്രിയയുടെ സവിശേഷത. പുതിയ ചീസ് ഒഴികെ ഭൂരിഭാഗം ചീസും പാകമാകും.
അഫിനേജ് (ബാൻഡ്): അഫ്ഫിനഗെ സെന്റ് പീറ്റേഴ്സ്ബർഗ് നഗരത്തിലെ സെലീന ലീഡ് ഗായകൻ മിഖായേൽ എം Kalinin ബാസ്സും താരം സെർജി സെര്ഗെഇഛ് ശിലിഅഎവ് 2012 ൽ സ്ഥാപിച്ച പ്രശസ്തമായ റഷ്യൻ ബാൻഡ് ആണ്. ബാൻഡ് അതിന്റേതായ നോയർ-ചാൻസൻ പാട്ടുകൾ ആലപിക്കുകയും അശുദ്ധമായ ഒരു ലോഹത്തെ ശുദ്ധീകരിക്കുന്ന പ്രക്രിയയിൽ നിന്ന് അതിന്റെ പേര് സ്വീകരിക്കുകയും ചെയ്യുന്നു.
ചീസ് വിളഞ്ഞത്: ചീസ് പാകമാകൽ , പകരമായി ചീസ് നീളുന്നു അല്ലെങ്കിൽ അഫിനേജ് , ചീസ് നിർമ്മാണത്തിലെ ഒരു പ്രക്രിയയാണ്. ചീസിലെ വ്യത്യസ്തമായ സ്വാദിന് ഇത് ഉത്തരവാദിയാണ്, കൂടാതെ " പാകമാകുന്ന ഏജന്റുമാരുടെ " പരിഷ്‌ക്കരണത്തിലൂടെ, രുചി, ഘടന, ശരീരം എന്നിങ്ങനെയുള്ള പലതരം പാൽക്കട്ടകളെ നിർവചിക്കുന്ന സവിശേഷതകൾ നിർണ്ണയിക്കുന്നു. "പാലിന്റെ ബാക്ടീരിയ, എൻസൈമുകൾ, ലാക്റ്റിക് സംസ്കാരം, റെനെറ്റ്, ലിപെയ്സുകൾ, ചേർത്ത അച്ചുകൾ അല്ലെങ്കിൽ യീസ്റ്റുകൾ, പാരിസ്ഥിതിക മലിനീകരണം" എന്നിവയുടെ ഏജന്റുമാരെ ഉൾക്കൊള്ളുന്ന സങ്കീർണ്ണമായ ശാരീരിക, രാസ, മൈക്രോബയോളജിക്കൽ മാറ്റങ്ങളുടെ ഒരു പരമ്പരയാണ് ഈ പ്രക്രിയയുടെ സവിശേഷത. പുതിയ ചീസ് ഒഴികെ ഭൂരിഭാഗം ചീസും പാകമാകും.
ബന്ധം: സംബന്ധം വിവക്ഷിക്കാനുപയോഗിക്കാറുണ്ട്:
ബന്ധം (നിയമം): നിയമം ൽ സാംസ്കാരിക നരവംശശാസ്ത്രം ൽ, സംബന്ധം സൃഷ്ടിച്ചു പരിഗണിക്കുകയില്ല ബന്ധം അല്ലെങ്കിൽ ഒരാളുടെ വിവാഹം ഫലമായി രണ്ടുപേർ തമ്മിൽ നിലനിൽക്കുന്ന. ഒരു വിവാഹത്തിലേക്കുള്ള ഓരോ കക്ഷിക്കും മറ്റ് പങ്കാളിയുടെ വിവാഹവുമായി ബന്ധമുണ്ടെങ്കിലും അത് വൈവാഹിക ബന്ധത്തെ തന്നെ ഉൾക്കൊള്ളുന്നില്ല. ബന്ധവുമായി ബന്ധപ്പെട്ട നിയമങ്ങളും പാരമ്പര്യങ്ങളും ആചാരങ്ങളും ഗണ്യമായി വ്യത്യാസപ്പെടുന്നു, ചിലപ്പോൾ വിവാഹ പങ്കാളികളിൽ ഒരാളുടെ മരണത്തോടെ ബന്ധം അവസാനിക്കുന്നു, ചിലപ്പോൾ വിവാഹ പങ്കാളികളുടെ വിവാഹമോചനവും അവസാനിക്കുന്നു. ദാമ്പത്യബന്ധത്തിലൂടെയുള്ള രക്തബന്ധത്തിന് പുറമേ, ദത്തെടുക്കൽ വഴിയോ അല്ലെങ്കിൽ ഒരു പടി ബന്ധം വഴിയോ "ബന്ധം" ചിലപ്പോൾ രക്തബന്ധം ഉൾപ്പെടുത്താം.
അഫൈൻ: അഫൈൻ കണക്ഷനുകളുമായോ അഫിനിറ്റികളുമായോ ബന്ധപ്പെട്ടിരിക്കുന്നു. ഇത് റഫർ ചെയ്യാം: അഫൈൻ, നിയമത്തിലും നരവംശശാസ്ത്രത്തിലും വിവാഹം കഴിച്ച ബന്ധു അഫൈൻ സിഫർ, കൂടുതൽ പൊതുവായ പകര സൈഫറിന്റെ പ്രത്യേക കേസ് അഫൈൻ കോമ്പിനേഷൻ, ഒരു പ്രത്യേക തരം നിയന്ത്രിത ലീനിയർ കോമ്പിനേഷൻ അഫൈൻ കണക്ഷൻ, വ്യത്യസ്‌ത മാനിഫോൾഡിന്റെ ടാൻജെന്റ് ബണ്ടിലിലെ കണക്ഷൻ അഫൈൻ കോർഡിനേറ്റ് സിസ്റ്റം, ഒരു കോർഡിനേറ്റ് സിസ്റ്റം, ഇത് ഒരു കാർട്ടീഷ്യൻ കോർഡിനേറ്റ് സിസ്റ്റമായി കാണാനാകും, അവിടെ അക്ഷങ്ങൾ സ്ഥാപിച്ചിട്ടുള്ളതിനാൽ അവ പരസ്പരം ഓർത്തഡോണലായിരിക്കില്ല. ടെൻസർ കാണുക. അഫൈൻ ഡിഫറൻഷ്യൽ ജ്യാമിതി, പ്രത്യേക അഫൈൻ ഗ്രൂപ്പിന്റെ പ്രവർത്തനത്തിന് കീഴിലുള്ള ഡിഫറൻഷ്യൽ മാറ്റങ്ങളെ പഠിക്കുന്ന ജ്യാമിതി സീക്വൻസ് അലൈൻമെന്റിനായി, പ്രത്യേകിച്ച് ബയോ ഇൻഫോർമാറ്റിക്സിൽ ഉപയോഗിക്കുന്ന ഏറ്റവും വ്യാപകമായി ഉപയോഗിക്കുന്ന സ്കോറിംഗ് ഫംഗ്ഷൻ അഫൈൻ ഗ്യാപ് പെനാൽറ്റി അഫൈൻ ജ്യാമിതി, സമാന്തര ലൈനുകളുടെ സ്വഭാവമുള്ള ജ്യാമിതി കെ എന്ന ഫീൽഡിനു മുകളിലുള്ള ഏതൊരു അഫൈൻ സ്പേസിൽ നിന്നുമുള്ള എല്ലാ വിപരീത അഫൈൻ പരിവർത്തനങ്ങളുടെയും ഗ്രൂപ്പായ അഫൈൻ ഗ്രൂപ്പ് സങ്കോചത്തിന്റെ ഘടനാപരമായ നിയമത്തെ നിരാകരിക്കുന്ന തെളിവ് സിദ്ധാന്തം അഫൈൻ ലോജിക് അഫൈൻ പ്രാതിനിധ്യം, തുടർച്ചയായ ഗ്രൂപ്പ് ഹോമോമോണിസം, അതിന്റെ മൂല്യങ്ങൾ ഒരു അഫൈൻ സ്പേസിന്റെ ഓട്ടോമോർഫിസങ്ങളാണ് കമ്മ്യൂട്ടേറ്റീവ് റിങ്ങിന്റെ പ്രധാന ആശയങ്ങളുടെ സ്പെക്ട്രമായ അഫൈൻ സ്കീം അഫൈൻ മോർഫിസം, ഒരു ഓപ്പൺ അഫൈൻ സബ്‌സ്‌കീമിന്റെ പ്രീ-ഇമേജ് അഫൈൻ ആയ സ്കീമുകളുടെ ഒരു മോർഫിസം യൂക്ലിഡിയൻ സ്പേസിന്റെ അഫൈൻ-ജ്യാമിതീയ സവിശേഷതകളെ സാമാന്യവൽക്കരിക്കുന്ന ഒരു അമൂർത്ത ഘടനയായ അഫൈൻ സ്പേസ് അഫൈൻ ടെൻസർ, ഒരു അഫൈൻ കോർഡിനേറ്റ് സിസ്റ്റത്തിന്റെ ടെൻസർ അഫൈൻ ട്രാൻസ്ഫോർമേഷൻ, വരികൾ തമ്മിലുള്ള സമാന്തരതയുടെ ബന്ധം സംരക്ഷിക്കുന്ന ഒരു പരിവർത്തനം
ജ്യാമിതി ഉറപ്പിക്കുക: ഗണിതശാസ്ത്രത്തിൽ, അകലത്തിന്റെയും കോണിന്റെയും മെട്രിക് സങ്കൽപ്പങ്ങൾ ഉപയോഗിക്കാതിരിക്കുമ്പോൾ യൂക്ലിഡിയൻ ജ്യാമിതിയുടെ അവശേഷിക്കുന്നത് അഫൈൻ ജ്യാമിതിയാണ് .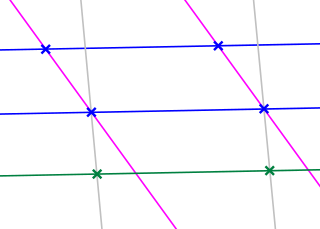
പരിവർത്തനം പരിവർത്തനം ചെയ്യുക: യൂക്ലിഡിയൻ ജ്യാമിതിയിൽ, വരികളും സമാന്തരതയും സംരക്ഷിക്കുന്ന ഒരു ജ്യാമിതീയ പരിവർത്തനമാണ് ഒരു അഫൈൻ പരിവർത്തനം അല്ലെങ്കിൽ ഒരു ബന്ധം .
അഫൈൻ-റെഗുലർ പോളിഗോൺ: ജ്യാമിതിയിൽ, ഒരു അഫൈൻ-റെഗുലർ പോളിഗോൺ അല്ലെങ്കിൽ അഫിനി റെഗുലർ പോളിഗോൺ എന്നത് ഒരു പോളിഗോൺ ആണ്, ഇത് ഒരു സാധാരണ പോളിഗോണുമായി ഒരു അഫൈൻ പരിവർത്തനത്തിലൂടെ ബന്ധപ്പെട്ടിരിക്കുന്നു. വിവർത്തനങ്ങൾ, ആകർഷകവും ആകർഷകമല്ലാത്തതുമായ സ്കെയിലിംഗ്, പ്രതിഫലനങ്ങൾ, ഭ്രമണങ്ങൾ, കത്രിക, മറ്റ് സമാനതകൾ എന്നിവയും ചിലത് ഉൾപ്പെടുന്നു, എന്നാൽ എല്ലാം രേഖീയ മാപ്പുകൾ അല്ല.
അഫൈൻ: അഫൈൻ കണക്ഷനുകളുമായോ അഫിനിറ്റികളുമായോ ബന്ധപ്പെട്ടിരിക്കുന്നു. ഇത് റഫർ ചെയ്യാം: അഫൈൻ, നിയമത്തിലും നരവംശശാസ്ത്രത്തിലും വിവാഹം കഴിച്ച ബന്ധു അഫൈൻ സിഫർ, കൂടുതൽ പൊതുവായ പകര സൈഫറിന്റെ പ്രത്യേക കേസ് അഫൈൻ കോമ്പിനേഷൻ, ഒരു പ്രത്യേക തരം നിയന്ത്രിത ലീനിയർ കോമ്പിനേഷൻ അഫൈൻ കണക്ഷൻ, വ്യത്യസ്‌ത മാനിഫോൾഡിന്റെ ടാൻജെന്റ് ബണ്ടിലിലെ കണക്ഷൻ അഫൈൻ കോർഡിനേറ്റ് സിസ്റ്റം, ഒരു കോർഡിനേറ്റ് സിസ്റ്റം, ഇത് ഒരു കാർട്ടീഷ്യൻ കോർഡിനേറ്റ് സിസ്റ്റമായി കാണാനാകും, അവിടെ അക്ഷങ്ങൾ സ്ഥാപിച്ചിട്ടുള്ളതിനാൽ അവ പരസ്പരം ഓർത്തഡോണലായിരിക്കില്ല. ടെൻസർ കാണുക. അഫൈൻ ഡിഫറൻഷ്യൽ ജ്യാമിതി, പ്രത്യേക അഫൈൻ ഗ്രൂപ്പിന്റെ പ്രവർത്തനത്തിന് കീഴിലുള്ള ഡിഫറൻഷ്യൽ മാറ്റങ്ങളെ പഠിക്കുന്ന ജ്യാമിതി സീക്വൻസ് അലൈൻമെന്റിനായി, പ്രത്യേകിച്ച് ബയോ ഇൻഫോർമാറ്റിക്സിൽ ഉപയോഗിക്കുന്ന ഏറ്റവും വ്യാപകമായി ഉപയോഗിക്കുന്ന സ്കോറിംഗ് ഫംഗ്ഷൻ അഫൈൻ ഗ്യാപ് പെനാൽറ്റി അഫൈൻ ജ്യാമിതി, സമാന്തര ലൈനുകളുടെ സ്വഭാവമുള്ള ജ്യാമിതി കെ എന്ന ഫീൽഡിനു മുകളിലുള്ള ഏതൊരു അഫൈൻ സ്പേസിൽ നിന്നുമുള്ള എല്ലാ വിപരീത അഫൈൻ പരിവർത്തനങ്ങളുടെയും ഗ്രൂപ്പായ അഫൈൻ ഗ്രൂപ്പ് സങ്കോചത്തിന്റെ ഘടനാപരമായ നിയമത്തെ നിരാകരിക്കുന്ന തെളിവ് സിദ്ധാന്തം അഫൈൻ ലോജിക് അഫൈൻ പ്രാതിനിധ്യം, തുടർച്ചയായ ഗ്രൂപ്പ് ഹോമോമോണിസം, അതിന്റെ മൂല്യങ്ങൾ ഒരു അഫൈൻ സ്പേസിന്റെ ഓട്ടോമോർഫിസങ്ങളാണ് കമ്മ്യൂട്ടേറ്റീവ് റിങ്ങിന്റെ പ്രധാന ആശയങ്ങളുടെ സ്പെക്ട്രമായ അഫൈൻ സ്കീം അഫൈൻ മോർഫിസം, ഒരു ഓപ്പൺ അഫൈൻ സബ്‌സ്‌കീമിന്റെ പ്രീ-ഇമേജ് അഫൈൻ ആയ സ്കീമുകളുടെ ഒരു മോർഫിസം യൂക്ലിഡിയൻ സ്പേസിന്റെ അഫൈൻ-ജ്യാമിതീയ സവിശേഷതകളെ സാമാന്യവൽക്കരിക്കുന്ന ഒരു അമൂർത്ത ഘടനയായ അഫൈൻ സ്പേസ് അഫൈൻ ടെൻസർ, ഒരു അഫൈൻ കോർഡിനേറ്റ് സിസ്റ്റത്തിന്റെ ടെൻസർ അഫൈൻ ട്രാൻസ്ഫോർമേഷൻ, വരികൾ തമ്മിലുള്ള സമാന്തരതയുടെ ബന്ധം സംരക്ഷിക്കുന്ന ഒരു പരിവർത്തനം
അഫൈൻ അനലിറ്റിക്‌സ്: സങ്കീർണ്ണമായ ബിസിനസ്സ് പ്രശ്‌നങ്ങൾ പരിഹരിക്കുന്നതിനായി ഹൈ-എൻഡ് അനലിറ്റിക്‌സ് സേവനങ്ങളുടെ ദാതാവാണ് അഫൈൻ അനലിറ്റിക്‌സ് . ന്യൂയോർക്ക്, യുണൈറ്റഡ് സ്റ്റേറ്റ്സ്, ഇന്ത്യയിലെ ബെംഗളൂരു എന്നിവിടങ്ങളിലായി ഏകദേശം 300 ആളുകളുണ്ട് അഫൈനിൽ.
കാർട്ടൻ മാട്രിക്സ്: ഗണിതശാസ്ത്രത്തിൽ, കാർട്ടൻ മാട്രിക്സ് എന്ന പദത്തിന് മൂന്ന് അർത്ഥങ്ങളുണ്ട്. ഇവയ്‌ക്കെല്ലാം ഫ്രഞ്ച് ഗണിതശാസ്ത്രജ്ഞൻ എലി കാർട്ടന്റെ പേരാണ് നൽകിയിരിക്കുന്നത്. രസകരമെന്നു പറയട്ടെ, ലീ ആൾജിബ്രയുടെ പശ്ചാത്തലത്തിലുള്ള കാർട്ടാൻ മെട്രിക്സുകൾ ആദ്യം അന്വേഷിച്ചത് വിൽഹെം കില്ലിംഗാണ്, അതേസമയം കില്ലിംഗ് ഫോം കാർട്ടാൻ മൂലമാണ്.
ഇടം ഉറപ്പാക്കുക: ഗണിതശാസ്ത്രത്തിൽ, യൂക്ലിഡിയൻ സ്പെയ്സുകളുടെ ചില ഗുണങ്ങളെ സാമാന്യവൽക്കരിക്കുന്ന ഒരു ജ്യാമിതീയ ഘടനയാണ് അഫൈൻ സ്പേസ് , ഇത് കോണുകളുടെ ദൂരവും അളവും എന്ന ആശയങ്ങളിൽ നിന്ന് വിഭിന്നമാണ്, സമാന്തരതയുമായി ബന്ധപ്പെട്ട ഗുണങ്ങളും സമാന്തരത്തിനായുള്ള നീളത്തിന്റെ അനുപാതവും മാത്രം നിലനിർത്തുന്നു ലൈൻ സെഗ്‌മെന്റുകൾ.
കോക്‌സെറ്റർ ഗ്രൂപ്പ്: ഗണിതശാസ്ത്രത്തിൽ, പ്രതിഫലനങ്ങളുടെ അടിസ്ഥാനത്തിൽ description പചാരിക വിവരണം അംഗീകരിക്കുന്ന ഒരു അമൂർത്ത ഗ്രൂപ്പാണ് എച്ച്എസ്എം കോക്സറ്ററിന്റെ പേരിലുള്ള ഒരു കോക്സറ്റർ ഗ്രൂപ്പ് . വാസ്തവത്തിൽ, പരിമിത കോക്സറ്റർ ഗ്രൂപ്പുകൾ കൃത്യമായി പരിമിത യൂക്ലിഡിയൻ പ്രതിഫലന ഗ്രൂപ്പുകളാണ്; സാധാരണ പോളിഹെഡ്രയുടെ സമമിതി ഗ്രൂപ്പുകൾ ഒരു ഉദാഹരണമാണ്. എന്നിരുന്നാലും, എല്ലാ കോക്സെറ്റർ ഗ്രൂപ്പുകളും പരിമിതമല്ല, എല്ലാം സമമിതികളുടെയും യൂക്ലിഡിയൻ പ്രതിഫലനങ്ങളുടെയും അടിസ്ഥാനത്തിൽ വിവരിക്കാനാവില്ല. കോക്‌സെറ്റർ ഗ്രൂപ്പുകളെ പ്രതിഫലന ഗ്രൂപ്പുകളുടെ സംഗ്രഹമായി അവതരിപ്പിച്ചു, പരിമിത കോക്‌സെറ്റർ ഗ്രൂപ്പുകളെ 1935 ൽ തരംതിരിച്ചു.
ഡൈൻ‌കിൻ ഡയഗ്രം: ലീ സിദ്ധാന്തത്തിന്റെ ഗണിതശാസ്ത്ര മേഖലയിൽ, യൂജിൻ ഡൈൻ‌കിൻ‌ എന്ന പേരിലുള്ള ഒരു ഡൈൻ‌കിൻ‌ ഡയഗ്രം , ചില അരികുകൾ‌ ഇരട്ടിയോ മൂന്നിരട്ടിയോ ഉള്ള ഒരു തരം ഗ്രാഫാണ്. ഒന്നിലധികം അരികുകൾ, ചില പരിമിതികൾക്കുള്ളിൽ, സംവിധാനം ചെയ്യുന്നു.
അഫൈൻ ഗ്രാസ്മാനിയൻ: ഗണിതശാസ്ത്രത്തിൽ ഒരു ഫീൽഡ് k മേൽ ബീജീയഘടനയെയാണ് G എന്ന ഗ്രൂപ്പിന്റെ അഫ്ഫിനെ ഗ്രഷ്മംനിഅന് ഒരു IND-പദ്ധതി-ജനകമായ ത്രിമാന പദ്ധതികൾ-ഏത് ലൂപ്പ് ഗ്രൂപ്പ് ജി (കെ) ഒരു പതാക മുറികൾ കരുതിയിരുന്നത് ഏത് വിവരിക്കുന്നു കഴിയും എന്ന ചൊലിമിത് ആണ് ജ്യാമിതീയ സാറ്റേക്ക് കറസ്പോണ്ടൻസ് എന്നറിയപ്പെടുന്ന ലാംഗ്ലാൻഡ് ഇരട്ട ഗ്രൂപ്പായ എൽ ജി യുടെ പ്രാതിനിധ്യ സിദ്ധാന്തം.
അഫൈൻ ഗ്രാസ്മാനിയൻ (മനിഫോൾഡ്): ഗണിതശാസ്ത്രത്തിൽ, അഫൈൻ ഗ്രാസ്മാനിയൻ എന്ന പദത്തിന്റെ രണ്ട് വ്യത്യസ്ത അർത്ഥങ്ങളുണ്ട്. ഒരെണ്ണത്തിൽ ഇത് R n ന്റെ എല്ലാ k- ഡൈമെൻഷണൽ അഫൈൻ ഉപമേഖലകളുടെ മനിഫോൾഡാണ്, മറ്റൊന്ന് formal പചാരിക ലോറന്റ് സീരീസിനെ അടിസ്ഥാനമാക്കിയുള്ള ഒരു ഗ്രൂപ്പ്-റിങ്ങിന്റെ ഘടകമാണ് ഗ്രാസ്മാനിയൻ.
അഫെൻ ഹെക്ക് ആൾജിബ്ര: ഗണിതശാസ്ത്രത്തിൽ, ഒരു അഫൈൻ വെയിൽ ഗ്രൂപ്പുമായി ബന്ധപ്പെട്ട ബീജഗണിതമാണ് ഹെഫി ആൾജിബ്ര , ഇത് മക്ഡൊണാൾഡിന്റെ പോളിനോമിയലുകൾക്കുള്ള മക്ഡൊണാൾഡിന്റെ നിരന്തരമായ term ഹത്തെ തെളിയിക്കാൻ ഉപയോഗിക്കാം.
അഫിൻ ലീ ആൾജിബ്ര: ഗണിതശാസ്ത്രത്തിൽ, ഒരു അഫൈൻ ലൈ ആൾജിബ്ര എന്നത് അനന്ത-ഡൈമൻഷണൽ ലൈ ആൾജിബ്രയാണ്, ഇത് ഒരു പരിമിത അളവിലുള്ള ലളിതമായ ആൾജിബ്രയിൽ നിന്ന് കാനോനിക്കൽ രീതിയിൽ നിർമ്മിച്ചിരിക്കുന്നു. ഇത് ഒരു കാക്-മൂഡി ആൾജിബ്രയാണ്, ഇതിനായി സാമാന്യവൽക്കരിച്ച കാർട്ടൂൺ മാട്രിക്സ് പോസിറ്റീവ് സെമി-ഡെഫിനിറ്റ് ആണ്, കൂടാതെ 1. പൂർണ്ണമായും ഗണിതശാസ്ത്ര വീക്ഷണകോണിൽ നിന്ന്, അഫൈൻ ലീ ആൾജിബ്രകൾ രസകരമാണ്, കാരണം അവയുടെ പ്രാതിനിധ്യ സിദ്ധാന്തം പരിമിത-ഡൈമൻഷണൽ സെമിസിംപിൾ ലൈയുടെ പ്രാതിനിധ്യ സിദ്ധാന്തം പോലെ ബീജഗണിതം, പൊതുവായ കാക്-മൂഡി ആൾജിബ്രകളേക്കാൾ നന്നായി മനസ്സിലാക്കാം. വിക്ടർ കാക് നിരീക്ഷിച്ചതുപോലെ, അഫൈൻ ലീ ആൾജിബ്രാസിന്റെ പ്രാതിനിധ്യത്തിനുള്ള പ്രതീക സൂത്രവാക്യം ചില കോമ്പിനേറ്റോറിയൽ ഐഡന്റിറ്റികളെ സൂചിപ്പിക്കുന്നു, മക്ഡൊണാൾഡ് ഐഡന്റിറ്റികൾ.
അഫിൻ ലീ ആൾജിബ്ര: ഗണിതശാസ്ത്രത്തിൽ, ഒരു അഫൈൻ ലൈ ആൾജിബ്ര എന്നത് അനന്ത-ഡൈമൻഷണൽ ലൈ ആൾജിബ്രയാണ്, ഇത് ഒരു പരിമിത അളവിലുള്ള ലളിതമായ ആൾജിബ്രയിൽ നിന്ന് കാനോനിക്കൽ രീതിയിൽ നിർമ്മിച്ചിരിക്കുന്നു. ഇത് ഒരു കാക്-മൂഡി ആൾജിബ്രയാണ്, ഇതിനായി സാമാന്യവൽക്കരിച്ച കാർട്ടൂൺ മാട്രിക്സ് പോസിറ്റീവ് സെമി-ഡെഫിനിറ്റ് ആണ്, കൂടാതെ 1. പൂർണ്ണമായും ഗണിതശാസ്ത്ര വീക്ഷണകോണിൽ നിന്ന്, അഫൈൻ ലീ ആൾജിബ്രകൾ രസകരമാണ്, കാരണം അവയുടെ പ്രാതിനിധ്യ സിദ്ധാന്തം പരിമിത-ഡൈമൻഷണൽ സെമിസിംപിൾ ലൈയുടെ പ്രാതിനിധ്യ സിദ്ധാന്തം പോലെ ബീജഗണിതം, പൊതുവായ കാക്-മൂഡി ആൾജിബ്രകളേക്കാൾ നന്നായി മനസ്സിലാക്കാം. വിക്ടർ കാക് നിരീക്ഷിച്ചതുപോലെ, അഫൈൻ ലീ ആൾജിബ്രാസിന്റെ പ്രാതിനിധ്യത്തിനുള്ള പ്രതീക സൂത്രവാക്യം ചില കോമ്പിനേറ്റോറിയൽ ഐഡന്റിറ്റികളെ സൂചിപ്പിക്കുന്നു, മക്ഡൊണാൾഡ് ഐഡന്റിറ്റികൾ.
അഫിൻ ലീ ആൾജിബ്ര: ഗണിതശാസ്ത്രത്തിൽ, ഒരു അഫൈൻ ലൈ ആൾജിബ്ര എന്നത് അനന്ത-ഡൈമൻഷണൽ ലൈ ആൾജിബ്രയാണ്, ഇത് ഒരു പരിമിത അളവിലുള്ള ലളിതമായ ആൾജിബ്രയിൽ നിന്ന് കാനോനിക്കൽ രീതിയിൽ നിർമ്മിച്ചിരിക്കുന്നു. ഇത് ഒരു കാക്-മൂഡി ആൾജിബ്രയാണ്, ഇതിനായി സാമാന്യവൽക്കരിച്ച കാർട്ടൂൺ മാട്രിക്സ് പോസിറ്റീവ് സെമി-ഡെഫിനിറ്റ് ആണ്, കൂടാതെ 1. പൂർണ്ണമായും ഗണിതശാസ്ത്ര വീക്ഷണകോണിൽ നിന്ന്, അഫൈൻ ലീ ആൾജിബ്രകൾ രസകരമാണ്, കാരണം അവയുടെ പ്രാതിനിധ്യ സിദ്ധാന്തം പരിമിത-ഡൈമൻഷണൽ സെമിസിംപിൾ ലൈയുടെ പ്രാതിനിധ്യ സിദ്ധാന്തം പോലെ ബീജഗണിതം, പൊതുവായ കാക്-മൂഡി ആൾജിബ്രകളേക്കാൾ നന്നായി മനസ്സിലാക്കാം. വിക്ടർ കാക് നിരീക്ഷിച്ചതുപോലെ, അഫൈൻ ലീ ആൾജിബ്രാസിന്റെ പ്രാതിനിധ്യത്തിനുള്ള പ്രതീക സൂത്രവാക്യം ചില കോമ്പിനേറ്റോറിയൽ ഐഡന്റിറ്റികളെ സൂചിപ്പിക്കുന്നു, മക്ഡൊണാൾഡ് ഐഡന്റിറ്റികൾ.
പരിവർത്തനം പരിവർത്തനം ചെയ്യുക: യൂക്ലിഡിയൻ ജ്യാമിതിയിൽ, വരികളും സമാന്തരതയും സംരക്ഷിക്കുന്ന ഒരു ജ്യാമിതീയ പരിവർത്തനമാണ് ഒരു അഫൈൻ പരിവർത്തനം അല്ലെങ്കിൽ ഒരു ബന്ധം .
കോക്‌സെറ്റർ ഗ്രൂപ്പ്: ഗണിതശാസ്ത്രത്തിൽ, പ്രതിഫലനങ്ങളുടെ അടിസ്ഥാനത്തിൽ description പചാരിക വിവരണം അംഗീകരിക്കുന്ന ഒരു അമൂർത്ത ഗ്രൂപ്പാണ് എച്ച്എസ്എം കോക്സറ്ററിന്റെ പേരിലുള്ള ഒരു കോക്സറ്റർ ഗ്രൂപ്പ് . വാസ്തവത്തിൽ, പരിമിത കോക്സറ്റർ ഗ്രൂപ്പുകൾ കൃത്യമായി പരിമിത യൂക്ലിഡിയൻ പ്രതിഫലന ഗ്രൂപ്പുകളാണ്; സാധാരണ പോളിഹെഡ്രയുടെ സമമിതി ഗ്രൂപ്പുകൾ ഒരു ഉദാഹരണമാണ്. എന്നിരുന്നാലും, എല്ലാ കോക്സെറ്റർ ഗ്രൂപ്പുകളും പരിമിതമല്ല, എല്ലാം സമമിതികളുടെയും യൂക്ലിഡിയൻ പ്രതിഫലനങ്ങളുടെയും അടിസ്ഥാനത്തിൽ വിവരിക്കാനാവില്ല. കോക്‌സെറ്റർ ഗ്രൂപ്പുകളെ പ്രതിഫലന ഗ്രൂപ്പുകളുടെ സംഗ്രഹമായി അവതരിപ്പിച്ചു, പരിമിത കോക്‌സെറ്റർ ഗ്രൂപ്പുകളെ 1935 ൽ തരംതിരിച്ചു.
പ്രവർത്തനം വ്യക്തമാക്കുക: അനുവദിക്കുക സെമിസിംപിൾ ആൾജിബ്രയുടെ വെയിൽ ഗ്രൂപ്പായിരിക്കുക . ലളിതമായ ഒരു കൂട്ടം വേരുകൾ ഉണ്ടെന്ന് കരുതുക തിരഞ്ഞെടുത്തു.
ആകൃതിയിലുള്ള പൊരുത്തപ്പെടുത്തൽ: ഒരു നിർദ്ദിഷ്ട ഇമേജ് പോയിന്റിലെ അയൽ‌പ്രദേശത്തെ പ്രാദേശിക ഇമേജ് ഘടനയിലേക്ക് സുഗമമായ കേർണലുകളുടെ ഒരു അഫൈൻ ഗ്രൂപ്പിലെ സുഗമമായ കേർണലുകളുടെ ആകൃതി ആവർത്തനമായി പൊരുത്തപ്പെടുത്തുന്നതിനുള്ള ഒരു രീതിയാണ് അഫൈൻ ഷേപ്പ് അഡാപ്റ്റേഷൻ . സമാനമായി, വാർ‌പ്പ്ഡ് ഇമേജ് പാച്ചുകളിൽ‌ ഭ്രമണപരമായി സമമിതി ഫിൽ‌റ്റർ‌ പ്രയോഗിക്കുമ്പോൾ‌ അഫൈൻ‌ രൂപാന്തരീകരണങ്ങളോടെ ഒരു പ്രാദേശിക ഇമേജ് പാച്ച് ആവർത്തിച്ച് വാർ‌പ്പ് ചെയ്യുന്നതിലൂടെ അഫൈൻ‌ ഷേപ്പ് അഡാപ്റ്റേഷൻ‌ പൂർ‌ത്തിയാക്കാൻ‌ കഴിയും. ഈ ആവർത്തന പ്രക്രിയ സംയോജിക്കുന്നുവെങ്കിൽ, തത്ഫലമായുണ്ടാകുന്ന നിശ്ചിത പോയിന്റ് അഫൈൻ മാറ്റമില്ലാത്തതായിരിക്കും . കമ്പ്യൂട്ടർ ദർശനത്തിന്റെ മേഖലയിൽ, അഫൈൻ മാറ്റമില്ലാത്ത പലിശ പോയിന്റ് ഓപ്പറേറ്റർമാരെയും അഫൈൻ മാറ്റമില്ലാത്ത ടെക്സ്ചർ വിശകലന രീതികളെയും നിർവചിക്കുന്നതിന് ഈ ആശയം ഉപയോഗിച്ചു.
ബീജഗണിതം: അഫൈൻ ബീജഗണിതത്തെ ഇനിപ്പറയുന്നവ പരാമർശിക്കാം: കാക്-മൂഡി ആൾജിബ്രകളുടെ ഒരു തരം അഫൈൻ ലൈ ആൾജിബ്ര അഫൈൻ ഗ്രൂപ്പിന്റെ ലീ ആൾജിബ്ര അവസാനമായി സൃഷ്ടിച്ച ബീജഗണിതം ഹെക്ക് ആൾജിബ്രയെ അഫൈൻ ചെയ്യുക
ബീജഗണിതം: അഫൈൻ ബീജഗണിതത്തെ ഇനിപ്പറയുന്നവ പരാമർശിക്കാം: കാക്-മൂഡി ആൾജിബ്രകളുടെ ഒരു തരം അഫൈൻ ലൈ ആൾജിബ്ര അഫൈൻ ഗ്രൂപ്പിന്റെ ലീ ആൾജിബ്ര അവസാനമായി സൃഷ്ടിച്ച ബീജഗണിതം ഹെക്ക് ആൾജിബ്രയെ അഫൈൻ ചെയ്യുക
ബീജഗണിത വക്രം: ഗണിതശാസ്ത്രത്തിൽ, രണ്ട് വേരിയബിളുകളിലുള്ള ഒരു പോളിനോമിയലിന്റെ പൂജ്യ ഗണമാണ് അഫൈൻ ബീജഗണിത തലം കർവ് . മൂന്ന് വേരിയബിളുകളിൽ ഒരു ഏകതാനമായ പോളിനോമിയലിന്റെ പ്രൊജക്റ്റീവ് തലം സജ്ജമാക്കിയ പൂജ്യമാണ് പ്രൊജക്റ്റീവ് ബീജഗണിത തലം കർവ് . ഒരു അഫൈൻ ബീജഗണിത തലം വളവ് ഒരു പ്രൊജക്റ്റീവ് ബീജഗണിത തലം വളവിൽ നിർവചിക്കുന്ന പോളിനോമിയലിനെ ഏകീകൃതമാക്കുന്നതിലൂടെ പൂർത്തിയാക്കാൻ കഴിയും. വിപരീതമായി, h ( x , y , t ) = 0 എന്ന ഏകതാന സമവാക്യത്തിന്റെ പ്രൊജക്റ്റീവ് ബീജഗണിത തലം വളവ് h ( x , y , 1) = 0 എന്ന സമവാക്യത്തിന്റെ അഫൈൻ ബീജഗണിത തലം വളവിലേക്ക് പരിമിതപ്പെടുത്താം. ഈ രണ്ട് പ്രവർത്തനങ്ങളും ഓരോന്നിനും വിപരീതമാണ്; അതിനാൽ, ബീജഗണിത തലം വളവ് എന്ന വാക്യം പലപ്പോഴും അഫൈൻ ആണോ അല്ലെങ്കിൽ പ്രൊജക്റ്റീവ് കേസാണോ എന്ന് വ്യക്തമായി വ്യക്തമാക്കാതെ ഉപയോഗിക്കുന്നു.
ലീനിയർ ബീജഗണിത ഗ്രൂപ്പ്: ഗണിതശാസ്ത്രത്തിൽ, വിപരീത ഗ്രൂപ്പിന്റെ ഒരു ഉപഗ്രൂപ്പാണ് ഒരു രേഖീയ ബീജഗണിത ഗ്രൂപ്പ് പോളിനോമിയൽ സമവാക്യങ്ങൾ നിർവചിക്കുന്ന മെട്രിക്സ്. ഒരു ഉദാഹരണം ഓർത്തോഗണൽ ഗ്രൂപ്പ്, ആപേക്ഷികത നിർവചിച്ചിരിക്കുന്നു എവിടെ ന്റെ ട്രാൻസ്പോസ് ആണ് .
ഹൈപ്പർ‌സർ‌ഫേസ്: ജ്യാമിതിയിൽ, ഹൈപ്പർപ്ലെയ്ൻ, പ്ലെയിൻ കർവ്, ഉപരിതലം എന്നിവയുടെ സങ്കല്പങ്ങളുടെ പൊതുവൽക്കരണമാണ് ഹൈപ്പർസർഫേസ് . മാനം ഒരു ആംബിയന്റ് ഇടം n, സാധാരണയായി ഒരു യൂക്ലിഡിയൻ, ഒരു അഫ്ഫിനെ സ്ഥലം അല്ലെങ്കിൽ ഒരു പ്രൊജെച്തിവെ സ്പചെ.ഹ്യ്പെര്സുര്ഫചെസ് പങ്ക്, ഒരു ത്രിമാന ബഹിരാകാശത്ത് പ്രതലങ്ങളിൽ ഉപയോഗിച്ച് ഉൾപ്പെടുത്തിയ ഏത് 1, - ഒരു ഹ്യ്പെര്സുര്ഫചെ ഒരു പെരുകിയിരിക്കുന്നു അല്ലെങ്കിൽ മാനം ഒരു ബീജീയ മുറികൾ N എന്ന , കുറഞ്ഞത് പ്രാദേശികമായും ചിലപ്പോൾ ആഗോളമായും ഒരൊറ്റ വ്യക്തമായ സമവാക്യം നിർവചിക്കുന്നതിന്റെ സ്വത്ത്.
അഫൈൻ വൈവിധ്യങ്ങൾ: ബീജീയജ്യാമിതി ൽ ഒരു അഫ്ഫിനെ മുറികൾ, അല്ലെങ്കിൽ അഫ്ഫിനെ ബീജീയ മുറികൾ, ഒരു അല്ഗെബ്രൈചല്ല്യ് അടച്ച ഫീൽഡ് k മേൽ n ഒരു പ്രധാന അനുയോജ്യമായ തയ്യാറാക്കുന്നതിനുള്ള കെ ഗുണകങ്ങളുടെയും കൊണ്ട് n വേരിയബിളുകളിലൊന്ന് ബഹുപദസമവാക്യങ്ങൾക്ക് ചില പരിബദ്ധഗ്രൂപ്പുകളെയും കുടുംബത്തിലെ അഫ്ഫിനെ സ്പേസ് കെ പൂജ്യം-പ്രഭവസ്ഥാനവും. ഒരു പ്രൈം ആദർശം സൃഷ്ടിക്കുന്നതിനുള്ള വ്യവസ്ഥ നീക്കംചെയ്താൽ, അത്തരമൊരു സെറ്റിനെ (അഫൈൻ) ബീജഗണിത സെറ്റ് എന്ന് വിളിക്കുന്നു. ഒരു അഫൈൻ ഇനത്തിന്റെ സരിസ്‌കി ഓപ്പൺ സബ്‌വാരിറ്റിയെ ക്വാസി-അഫൈൻ ഇനം എന്ന് വിളിക്കുന്നു.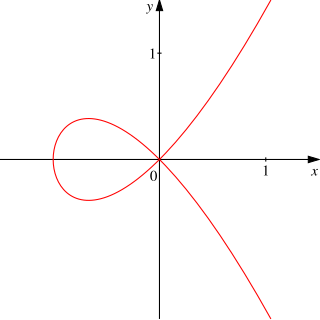
അഫൈൻ വൈവിധ്യങ്ങൾ: ബീജീയജ്യാമിതി ൽ ഒരു അഫ്ഫിനെ മുറികൾ, അല്ലെങ്കിൽ അഫ്ഫിനെ ബീജീയ മുറികൾ, ഒരു അല്ഗെബ്രൈചല്ല്യ് അടച്ച ഫീൽഡ് k മേൽ n ഒരു പ്രധാന അനുയോജ്യമായ തയ്യാറാക്കുന്നതിനുള്ള കെ ഗുണകങ്ങളുടെയും കൊണ്ട് n വേരിയബിളുകളിലൊന്ന് ബഹുപദസമവാക്യങ്ങൾക്ക് ചില പരിബദ്ധഗ്രൂപ്പുകളെയും കുടുംബത്തിലെ അഫ്ഫിനെ സ്പേസ് കെ പൂജ്യം-പ്രഭവസ്ഥാനവും. ഒരു പ്രൈം ആദർശം സൃഷ്ടിക്കുന്നതിനുള്ള വ്യവസ്ഥ നീക്കംചെയ്താൽ, അത്തരമൊരു സെറ്റിനെ (അഫൈൻ) ബീജഗണിത സെറ്റ് എന്ന് വിളിക്കുന്നു. ഒരു അഫൈൻ ഇനത്തിന്റെ സരിസ്‌കി ഓപ്പൺ സബ്‌വാരിറ്റിയെ ക്വാസി-അഫൈൻ ഇനം എന്ന് വിളിക്കുന്നു.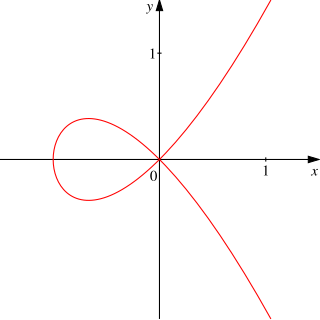
ലീനിയർ ഏകദേശ കണക്ക്: ഗണിതശാസ്ത്രത്തിൽ, ഒരു രേഖീയ പ്രവർത്തനം ഉപയോഗിച്ച് ഒരു പൊതു ഫംഗ്ഷന്റെ ഏകദേശമാണ് ഒരു രേഖീയ ഏകദേശീകരണം. സമവാക്യങ്ങളുടെ പരിഹാരങ്ങൾ പരിഹരിക്കുന്നതിനോ ഏകദേശമാക്കുന്നതിനോ ഉള്ള ആദ്യ ഓർഡർ രീതികൾ നിർമ്മിക്കുന്നതിന് പരിമിതമായ വ്യത്യാസങ്ങളുടെ രീതിയിൽ അവ വ്യാപകമായി ഉപയോഗിക്കുന്നു.
വക്രത ഉറപ്പിക്കുക: പ്രത്യേക അഫൈൻ വക്രത , ഇക്വാഫൈൻ വക്രത അല്ലെങ്കിൽ അഫൈൻ വക്രത എന്നും അറിയപ്പെടുന്നു, ഇത് ഒരു പ്രത്യേക തരം വക്രതയാണ്, ഇത് ഒരു തലം വളവിൽ നിർവചിക്കപ്പെടുന്നു, അത് ഒരു പ്രത്യേക അഫൈൻ പരിവർത്തനത്തിന് കീഴിൽ മാറ്റമില്ല. സ്ഥിരമായ ഇക്വാഫൈൻ വക്രത k യുടെ വക്രങ്ങൾ കൃത്യമായി എല്ലാ നോൺ-സിംഗുലർ പ്ലെയിൻ കോണിക്സുകളാണ്. K > 0 ഉള്ളവർ ദീർഘവൃത്തങ്ങളാണ്, k = 0 ഉള്ളവർ പരാബോളകളാണ്, k <0 ഉള്ളവർ ഹൈപ്പർബോളകളാണ്.
വക്രത ഉറപ്പിക്കുക: പ്രത്യേക അഫൈൻ വക്രത , ഇക്വാഫൈൻ വക്രത അല്ലെങ്കിൽ അഫൈൻ വക്രത എന്നും അറിയപ്പെടുന്നു, ഇത് ഒരു പ്രത്യേക തരം വക്രതയാണ്, ഇത് ഒരു തലം വളവിൽ നിർവചിക്കപ്പെടുന്നു, അത് ഒരു പ്രത്യേക അഫൈൻ പരിവർത്തനത്തിന് കീഴിൽ മാറ്റമില്ല. സ്ഥിരമായ ഇക്വാഫൈൻ വക്രത k യുടെ വക്രങ്ങൾ കൃത്യമായി എല്ലാ നോൺ-സിംഗുലർ പ്ലെയിൻ കോണിക്സുകളാണ്. K > 0 ഉള്ളവർ ദീർഘവൃത്തങ്ങളാണ്, k = 0 ഉള്ളവർ പരാബോളകളാണ്, k <0 ഉള്ളവർ ഹൈപ്പർബോളകളാണ്.
അഫിൻ അരിത്മെറ്റിക്: സ്വയം സാധൂകരിച്ച സംഖ്യാ വിശകലനത്തിനുള്ള ഒരു മാതൃകയാണ് അഫൈൻ അരിത്മെറ്റിക് ( AA ). AA- യിൽ, താൽപ്പര്യത്തിന്റെ അളവുകൾ ചില പ്രാകൃത വേരിയബിളുകളുടെ അഫൈൻ കോമ്പിനേഷനുകളായി പ്രതിനിധീകരിക്കുന്നു, ഇത് ഡാറ്റയിലെ അനിശ്ചിതത്വത്തിന്റെ ഉറവിടങ്ങൾ അല്ലെങ്കിൽ കണക്കുകൂട്ടൽ സമയത്ത് നടത്തിയ ഏകദേശ കണക്കുകൾ.
ഇടം ഉറപ്പാക്കുക: ഗണിതശാസ്ത്രത്തിൽ, യൂക്ലിഡിയൻ സ്പെയ്സുകളുടെ ചില ഗുണങ്ങളെ സാമാന്യവൽക്കരിക്കുന്ന ഒരു ജ്യാമിതീയ ഘടനയാണ് അഫൈൻ സ്പേസ് , ഇത് കോണുകളുടെ ദൂരവും അളവും എന്ന ആശയങ്ങളിൽ നിന്ന് വിഭിന്നമാണ്, സമാന്തരതയുമായി ബന്ധപ്പെട്ട ഗുണങ്ങളും സമാന്തരത്തിനായുള്ള നീളത്തിന്റെ അനുപാതവും മാത്രം നിലനിർത്തുന്നു ലൈൻ സെഗ്‌മെന്റുകൾ.
ബ്രെയ്ഡ് ഗ്രൂപ്പ് അഫൈൻ ചെയ്യുക: ഗണിതശാസ്ത്രത്തിൽ, ഒരു അഫൈൻ കോക്സെറ്റർ സിസ്റ്റവുമായി ബന്ധപ്പെട്ട ഒരു ബ്രെയ്ഡ് ഗ്രൂപ്പാണ് അഫൈൻ ബ്രെയ്ഡ് ഗ്രൂപ്പ് . അവരുടെ ഗ്രൂപ്പ് വളയങ്ങളിൽ അഫൈൻ ഹെക്ക് ആൾജിബ്രാസ് എന്ന് വിളിക്കപ്പെടുന്ന ഘടകങ്ങളുണ്ട്. അവ ഇരട്ട അഫൈൻ ബ്രെയ്ഡ് ഗ്രൂപ്പുകളുടെ ഉപഗ്രൂപ്പുകളാണ്.
അഫൈൻ ബണ്ടിൽ: ഗണിതശാസ്ത്രത്തിൽ, ഒരു ഫൈബർ ബണ്ടിൽ ആണ് അഫൈൻ ബണ്ടിൽ , അതിന്റെ സാധാരണ ഫൈബർ, നാരുകൾ, ട്രിവിയലൈസേഷൻ മോർഫിസങ്ങൾ, സംക്രമണ പ്രവർത്തനങ്ങൾ എന്നിവ അഫൈൻ ആണ്.
സിംപ്ലക്സ്: ജ്യാമിതിയിൽ, ഒരു ത്രികോണം അല്ലെങ്കിൽ ടെട്രഹെഡ്രോൺ എന്ന ആശയം അനിയന്ത്രിതമായ അളവുകളിലേക്കുള്ള സാമാന്യവൽക്കരണമാണ് സിംപ്ലക്സ് . ഏതൊരു സ്ഥലത്തും സാധ്യമായ ഏറ്റവും ലളിതമായ പോളിറ്റോപ്പിനെ പ്രതിനിധീകരിക്കുന്നതിനാൽ സിംപ്ലക്‌സിന് ഈ പേര് നൽകിയിട്ടുണ്ട്.
അഫൈൻ സിഫർ: ഒരു അക്ഷരമാലയിലെ ഓരോ അക്ഷരങ്ങളും അതിന്റെ സംഖ്യാ തുല്യതയിലേക്ക് മാപ്പുചെയ്യുകയും ലളിതമായ ഗണിതശാസ്ത്ര പ്രവർത്തനം ഉപയോഗിച്ച് എൻ‌ക്രിപ്റ്റ് ചെയ്യുകയും ഒരു അക്ഷരത്തിലേക്ക് പരിവർത്തനം ചെയ്യുകയും ചെയ്യുന്ന ഒരു തരം മോണോഅൽഫാബെറ്റിക് പകരക്കാരനായ സൈഫറാണ് അഫൈൻ സൈഫർ. ഉപയോഗിച്ച സൂത്രവാക്യം അർത്ഥമാക്കുന്നത് ഓരോ അക്ഷരവും മറ്റൊരു അക്ഷരത്തിലേക്ക് എൻ‌ക്രിപ്റ്റ് ചെയ്യുന്നു, വീണ്ടും വീണ്ടും, അതായത് സൈഫർ അടിസ്ഥാനപരമായി ഒരു സ്റ്റാൻ‌ഡേർഡ് പകരക്കാരനായ സൈഫറാണ്, ഏത് അക്ഷരമാണ് ഏത് അക്ഷരത്തിലേക്ക് പോകുന്നത് എന്ന് നിയന്ത്രിക്കുന്നു. അതുപോലെ, ഇതിന് പകരമുള്ള എല്ലാ സൈഫറുകളുടെയും ബലഹീനതകളുണ്ട്. ഓരോ അക്ഷരവും ( കോടാലി + ബി ) മോഡ് 26 എന്ന ഫംഗ്ഷനുമായി ബന്ധിപ്പിച്ചിരിക്കുന്നു, ഇവിടെ b എന്നത് ഷിഫ്റ്റിന്റെ വ്യാപ്തിയാണ്.
അഫൈൻ കോമ്പിനേഷൻ: ഗണിതശാസ്ത്രം, X 1 ഒരു അഫ്ഫിനെ സംയുക്തമായും, ..., x n ഒരു ലീനിയർ സംയോജനമാണ്
സങ്കീർണ്ണ തലം: ഗണിതശാസ്ത്രത്തിൽ, യഥാർത്ഥ അച്ചുതണ്ടും ലംബമായ സാങ്കൽപ്പിക അക്ഷവും സ്ഥാപിച്ച സങ്കീർണ്ണ സംഖ്യകളുടെ ജ്യാമിതീയ പ്രാതിനിധ്യമാണ് സങ്കീർണ്ണ തലം അല്ലെങ്കിൽ z- പ്ലെയിൻ . ഇത് ഒരു പരിഷ്കരിച്ച കാർട്ടീഷ്യൻ തലം എന്ന് കണക്കാക്കാം, സങ്കീർണ്ണ സംഖ്യയുടെ യഥാർത്ഥ ഭാഗം x- അക്ഷത്തിൽ ഒരു സ്ഥാനചലനം പ്രതിനിധീകരിക്കുന്നു, സാങ്കൽപ്പിക ഭാഗം y- അക്ഷത്തിൽ ഒരു സ്ഥാനചലനം വഴി പ്രതിനിധീകരിക്കുന്നു.
കോൺവെക്സ് കോൺ: ലീനിയർ ആൾജിബ്രയിൽ, പോസിറ്റീവ് കോഫിഫിഷ്യന്റുകളുമായുള്ള ലീനിയർ കോമ്പിനേഷനുകളിൽ അടച്ചിരിക്കുന്ന ഒരു ഓർഡർ ചെയ്ത ഫീൽഡിന് മുകളിലുള്ള വെക്റ്റർ സ്പേസിന്റെ ഉപസെറ്റാണ് കോൺവെക്സ് കോൺ .
കണക്ഷൻ ഉറപ്പാക്കുക: ഡിഫറൻഷ്യൽ ജ്യാമിതിയിൽ, സമീപത്തുള്ള ടാൻജെന്റ് സ്‌പെയ്‌സുകളെ ബന്ധിപ്പിക്കുന്ന സുഗമമായ മാനിഫോൾഡിലെ ജ്യാമിതീയ വസ്‌തുവാണ് അഫൈൻ കണക്ഷൻ , അതിനാൽ ഒരു നിശ്ചിത വെക്റ്റർ സ്‌പെയ്‌സിലെ മൂല്യങ്ങളുള്ള മാനിഫോൾഡിലെ ഫംഗ്ഷനുകൾ പോലെ ടാൻജെന്റ് വെക്റ്റർ ഫീൽഡുകൾ വേർതിരിക്കാൻ ഇത് അനുവദിക്കുന്നു. പത്തൊൻപതാം നൂറ്റാണ്ടിലെ ജ്യാമിതിയിലും ടെൻസർ കാൽക്കുലസിലും ഒരു അഫൈൻ കണക്ഷന്റെ സങ്കല്പത്തിന്റെ വേരുകളുണ്ട്, എന്നാൽ 1920 കളുടെ ആരംഭം വരെ എലി കാർട്ടനും ഹെർമൻ വെയിലും ഇത് പൂർണ്ണമായി വികസിപ്പിച്ചില്ല. സങ്കേതഭാഷ ചര്തന് കാരണം ആണ് യൂക്ലിഡിയൻ R ഇവിടെ n പരിഭാഷ ടാഞ്ചെന്റ് ഇടങ്ങൾ തിരിച്ചറിയൽ അതിന്റെ ഉത്ഭവം ഉണ്ട്: ആശയം അഫ്ഫിനെ കണക്ഷൻ ഒരു നിര മാത്രമല്ല സുഗമമായി ഇന്ഫിനിതെസിമല്ല്യ് യൂക്ലിഡിയൻ ഒരു പെരുകിയിരിക്കുന്നു നോക്കുക എന്നതാണ്, എന്നാൽ ഒരു അഫ്ഫിനെ ആയി .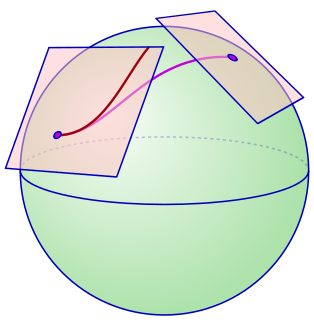
അഫൈൻ വൈവിധ്യങ്ങൾ: ബീജീയജ്യാമിതി ൽ ഒരു അഫ്ഫിനെ മുറികൾ, അല്ലെങ്കിൽ അഫ്ഫിനെ ബീജീയ മുറികൾ, ഒരു അല്ഗെബ്രൈചല്ല്യ് അടച്ച ഫീൽഡ് k മേൽ n ഒരു പ്രധാന അനുയോജ്യമായ തയ്യാറാക്കുന്നതിനുള്ള കെ ഗുണകങ്ങളുടെയും കൊണ്ട് n വേരിയബിളുകളിലൊന്ന് ബഹുപദസമവാക്യങ്ങൾക്ക് ചില പരിബദ്ധഗ്രൂപ്പുകളെയും കുടുംബത്തിലെ അഫ്ഫിനെ സ്പേസ് കെ പൂജ്യം-പ്രഭവസ്ഥാനവും. ഒരു പ്രൈം ആദർശം സൃഷ്ടിക്കുന്നതിനുള്ള വ്യവസ്ഥ നീക്കംചെയ്താൽ, അത്തരമൊരു സെറ്റിനെ (അഫൈൻ) ബീജഗണിത സെറ്റ് എന്ന് വിളിക്കുന്നു. ഒരു അഫൈൻ ഇനത്തിന്റെ സരിസ്‌കി ഓപ്പൺ സബ്‌വാരിറ്റിയെ ക്വാസി-അഫൈൻ ഇനം എന്ന് വിളിക്കുന്നു.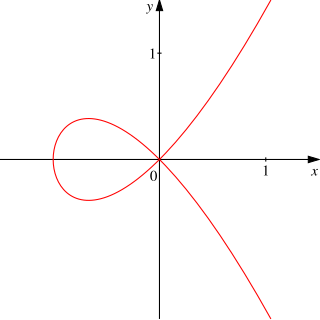
ഇടം ഉറപ്പാക്കുക: ഗണിതശാസ്ത്രത്തിൽ, യൂക്ലിഡിയൻ സ്പെയ്സുകളുടെ ചില ഗുണങ്ങളെ സാമാന്യവൽക്കരിക്കുന്ന ഒരു ജ്യാമിതീയ ഘടനയാണ് അഫൈൻ സ്പേസ് , ഇത് കോണുകളുടെ ദൂരവും അളവും എന്ന ആശയങ്ങളിൽ നിന്ന് വിഭിന്നമാണ്, സമാന്തരതയുമായി ബന്ധപ്പെട്ട ഗുണങ്ങളും സമാന്തരത്തിനായുള്ള നീളത്തിന്റെ അനുപാതവും മാത്രം നിലനിർത്തുന്നു ലൈൻ സെഗ്‌മെന്റുകൾ.
ഇടം ഉറപ്പാക്കുക: ഗണിതശാസ്ത്രത്തിൽ, യൂക്ലിഡിയൻ സ്പെയ്സുകളുടെ ചില ഗുണങ്ങളെ സാമാന്യവൽക്കരിക്കുന്ന ഒരു ജ്യാമിതീയ ഘടനയാണ് അഫൈൻ സ്പേസ് , ഇത് കോണുകളുടെ ദൂരവും അളവും എന്ന ആശയങ്ങളിൽ നിന്ന് വിഭിന്നമാണ്, സമാന്തരതയുമായി ബന്ധപ്പെട്ട ഗുണങ്ങളും സമാന്തരത്തിനായുള്ള നീളത്തിന്റെ അനുപാതവും മാത്രം നിലനിർത്തുന്നു ലൈൻ സെഗ്‌മെന്റുകൾ.
ബീജഗണിത ജ്യാമിതിയുടെ ഗ്ലോസറി: ബീജഗണിത ജ്യാമിതിയുടെ ഗ്ലോസറിയാണിത് .
വക്രത ഉറപ്പിക്കുക: പ്രത്യേക അഫൈൻ വക്രത , ഇക്വാഫൈൻ വക്രത അല്ലെങ്കിൽ അഫൈൻ വക്രത എന്നും അറിയപ്പെടുന്നു, ഇത് ഒരു പ്രത്യേക തരം വക്രതയാണ്, ഇത് ഒരു തലം വളവിൽ നിർവചിക്കപ്പെടുന്നു, അത് ഒരു പ്രത്യേക അഫൈൻ പരിവർത്തനത്തിന് കീഴിൽ മാറ്റമില്ല. സ്ഥിരമായ ഇക്വാഫൈൻ വക്രത k യുടെ വക്രങ്ങൾ കൃത്യമായി എല്ലാ നോൺ-സിംഗുലർ പ്ലെയിൻ കോണിക്സുകളാണ്. K > 0 ഉള്ളവർ ദീർഘവൃത്തങ്ങളാണ്, k = 0 ഉള്ളവർ പരാബോളകളാണ്, k <0 ഉള്ളവർ ഹൈപ്പർബോളകളാണ്.
ബീജഗണിത ഇനം: ഗണിതശാസ്ത്രത്തിന്റെ ഉപമേഖലയായ ബീജഗണിത ജ്യാമിതിയിലെ പഠനത്തിന്റെ കേന്ദ്ര വസ്‌തുക്കളാണ് ബീജഗണിത ഇനങ്ങൾ . ക്ലാസിക്കലായി, ഒരു ബീജഗണിത വൈവിധ്യത്തെ യഥാർത്ഥ അല്ലെങ്കിൽ സങ്കീർണ്ണ സംഖ്യകളെക്കാൾ പോളിനോമിയൽ സമവാക്യങ്ങളുടെ പരിഹാരങ്ങളുടെ കൂട്ടമായി നിർവചിച്ചിരിക്കുന്നു. യഥാർത്ഥ നിർവചനത്തിന് പിന്നിലുള്ള ജ്യാമിതീയ അവബോധം സംരക്ഷിക്കാൻ ശ്രമിക്കുമ്പോൾ ആധുനിക നിർവചനങ്ങൾ ഈ ആശയത്തെ പലവിധത്തിൽ സാമാന്യവൽക്കരിക്കുന്നു.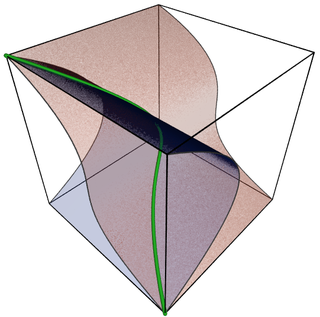
അഫൈൻ സിഫർ: ഒരു അക്ഷരമാലയിലെ ഓരോ അക്ഷരങ്ങളും അതിന്റെ സംഖ്യാ തുല്യതയിലേക്ക് മാപ്പുചെയ്യുകയും ലളിതമായ ഗണിതശാസ്ത്ര പ്രവർത്തനം ഉപയോഗിച്ച് എൻ‌ക്രിപ്റ്റ് ചെയ്യുകയും ഒരു അക്ഷരത്തിലേക്ക് പരിവർത്തനം ചെയ്യുകയും ചെയ്യുന്ന ഒരു തരം മോണോഅൽഫാബെറ്റിക് പകരക്കാരനായ സൈഫറാണ് അഫൈൻ സൈഫർ. ഉപയോഗിച്ച സൂത്രവാക്യം അർത്ഥമാക്കുന്നത് ഓരോ അക്ഷരവും മറ്റൊരു അക്ഷരത്തിലേക്ക് എൻ‌ക്രിപ്റ്റ് ചെയ്യുന്നു, വീണ്ടും വീണ്ടും, അതായത് സൈഫർ അടിസ്ഥാനപരമായി ഒരു സ്റ്റാൻ‌ഡേർഡ് പകരക്കാരനായ സൈഫറാണ്, ഏത് അക്ഷരമാണ് ഏത് അക്ഷരത്തിലേക്ക് പോകുന്നത് എന്ന് നിയന്ത്രിക്കുന്നു. അതുപോലെ, ഇതിന് പകരമുള്ള എല്ലാ സൈഫറുകളുടെയും ബലഹീനതകളുണ്ട്. ഓരോ അക്ഷരവും ( കോടാലി + ബി ) മോഡ് 26 എന്ന ഫംഗ്ഷനുമായി ബന്ധിപ്പിച്ചിരിക്കുന്നു, ഇവിടെ b എന്നത് ഷിഫ്റ്റിന്റെ വ്യാപ്തിയാണ്.
രൂപഭേദം (ഭൗതികശാസ്ത്രം): ഭൗതികശാസ്ത്രത്തിൽ രൂപമാകാൻ ഒരു റഫറൻസ് ക്രമീകരണം നിന്ന് ഒരു നിലവിലെ കോൺഫിഗറേഷൻ ഒരു ശരീരത്തിന്റെ ചൊംതിനുഉമ് മെക്കാനിക്സ് പരിവര്ത്തനം. ശരീരത്തിലെ എല്ലാ കണങ്ങളുടെയും സ്ഥാനങ്ങൾ അടങ്ങിയ ഒരു കൂട്ടമാണ് കോൺഫിഗറേഷൻ.
ഇടം ഉറപ്പാക്കുക: ഗണിതശാസ്ത്രത്തിൽ, യൂക്ലിഡിയൻ സ്പെയ്സുകളുടെ ചില ഗുണങ്ങളെ സാമാന്യവൽക്കരിക്കുന്ന ഒരു ജ്യാമിതീയ ഘടനയാണ് അഫൈൻ സ്പേസ് , ഇത് കോണുകളുടെ ദൂരവും അളവും എന്ന ആശയങ്ങളിൽ നിന്ന് വിഭിന്നമാണ്, സമാന്തരതയുമായി ബന്ധപ്പെട്ട ഗുണങ്ങളും സമാന്തരത്തിനായുള്ള നീളത്തിന്റെ അനുപാതവും മാത്രം നിലനിർത്തുന്നു ലൈൻ സെഗ്‌മെന്റുകൾ.
ഡിഫറൻഷ്യൽ ജ്യാമിതി വ്യക്തമാക്കുക: ഒരു തരം ഡിഫറൻഷ്യൽ ജ്യാമിതിയാണ് അഫൈൻ ഡിഫറൻഷ്യൽ ജ്യാമിതി , അതിൽ വോളിയം സംരക്ഷിക്കുന്ന അഫൈൻ പരിവർത്തനങ്ങൾക്ക് കീഴിൽ ഡിഫറൻഷ്യൽ അസ്ഥിരങ്ങൾ മാറ്റമില്ല. ക്ലീന്റെ എർലാഞ്ചൻ പ്രോഗ്രാമിൽ നിന്ന് അഫൈൻ ഡിഫറൻഷ്യൽ ജ്യാമിതി എന്ന പേര് പിന്തുടരുന്നു. അഫൈനും റിമാനിയൻ ഡിഫറൻഷ്യൽ ജ്യാമിതിയും തമ്മിലുള്ള അടിസ്ഥാന വ്യത്യാസം, അഫൈൻ കേസിൽ ഞങ്ങൾ അളവുകൾക്ക് പകരം വോളിയം ഫോമുകൾ ഒരു മനിഫോൾഡിലൂടെ അവതരിപ്പിക്കുന്നു എന്നതാണ്.
അഫൈൻ സിഫർ: ഒരു അക്ഷരമാലയിലെ ഓരോ അക്ഷരങ്ങളും അതിന്റെ സംഖ്യാ തുല്യതയിലേക്ക് മാപ്പുചെയ്യുകയും ലളിതമായ ഗണിതശാസ്ത്ര പ്രവർത്തനം ഉപയോഗിച്ച് എൻ‌ക്രിപ്റ്റ് ചെയ്യുകയും ഒരു അക്ഷരത്തിലേക്ക് പരിവർത്തനം ചെയ്യുകയും ചെയ്യുന്ന ഒരു തരം മോണോഅൽഫാബെറ്റിക് പകരക്കാരനായ സൈഫറാണ് അഫൈൻ സൈഫർ. ഉപയോഗിച്ച സൂത്രവാക്യം അർത്ഥമാക്കുന്നത് ഓരോ അക്ഷരവും മറ്റൊരു അക്ഷരത്തിലേക്ക് എൻ‌ക്രിപ്റ്റ് ചെയ്യുന്നു, വീണ്ടും വീണ്ടും, അതായത് സൈഫർ അടിസ്ഥാനപരമായി ഒരു സ്റ്റാൻ‌ഡേർഡ് പകരക്കാരനായ സൈഫറാണ്, ഏത് അക്ഷരമാണ് ഏത് അക്ഷരത്തിലേക്ക് പോകുന്നത് എന്ന് നിയന്ത്രിക്കുന്നു. അതുപോലെ, ഇതിന് പകരമുള്ള എല്ലാ സൈഫറുകളുടെയും ബലഹീനതകളുണ്ട്. ഓരോ അക്ഷരവും ( കോടാലി + ബി ) മോഡ് 26 എന്ന ഫംഗ്ഷനുമായി ബന്ധിപ്പിച്ചിരിക്കുന്നു, ഇവിടെ b എന്നത് ഷിഫ്റ്റിന്റെ വ്യാപ്തിയാണ്.
ഫോക്കൽ സെറ്റ് അഫൈൻ ചെയ്യുക: ഗണിതശാസ്ത്രത്തിലും, പ്രത്യേകിച്ച് അഫൈൻ ഡിഫറൻഷ്യൽ ജ്യാമിതിയിലും, സുഗമമായ മാനിഫോൾഡ് N- ൽ ഉൾച്ചേർത്ത മിനുസമാർന്ന സബ്മാനിഫോൾഡ് M- ന്റെ അഫൈൻ ഫോക്കൽ സെറ്റ് അഫൈൻ സാധാരണ വരികൾ സൃഷ്ടിക്കുന്ന കാസ്റ്റിക് ആണ്. ഒരു നിശ്ചിത കുടുംബത്തിന്റെ വിഭജന സെറ്റായി ഇത് മനസ്സിലാക്കാനാകും. കുടുംബത്തിന്റെ പാരാമീറ്റർ മൂല്യങ്ങളുടെ ഗണമാണ് വിഭജന സെറ്റ്, അത് അധ enera പതിച്ച സിംഗുലാരിറ്റികളുമായി പ്രവർത്തിക്കുന്നു. ഇത് ചലനാത്മക സിസ്റ്റങ്ങളിലെ വിഭജന രേഖാചിത്രത്തിന് സമാനമല്ല.
ഇടം ഉറപ്പാക്കുക: ഗണിതശാസ്ത്രത്തിൽ, യൂക്ലിഡിയൻ സ്പെയ്സുകളുടെ ചില ഗുണങ്ങളെ സാമാന്യവൽക്കരിക്കുന്ന ഒരു ജ്യാമിതീയ ഘടനയാണ് അഫൈൻ സ്പേസ് , ഇത് കോണുകളുടെ ദൂരവും അളവും എന്ന ആശയങ്ങളിൽ നിന്ന് വിഭിന്നമാണ്, സമാന്തരതയുമായി ബന്ധപ്പെട്ട ഗുണങ്ങളും സമാന്തരത്തിനായുള്ള നീളത്തിന്റെ അനുപാതവും മാത്രം നിലനിർത്തുന്നു ലൈൻ സെഗ്‌മെന്റുകൾ.
പരിവർത്തനം പരിവർത്തനം ചെയ്യുക: യൂക്ലിഡിയൻ ജ്യാമിതിയിൽ, വരികളും സമാന്തരതയും സംരക്ഷിക്കുന്ന ഒരു ജ്യാമിതീയ പരിവർത്തനമാണ് ഒരു അഫൈൻ പരിവർത്തനം അല്ലെങ്കിൽ ഒരു ബന്ധം .
അഫൈൻ ഗേജ് സിദ്ധാന്തം: ക്ലാസിക്കൽ ഗേജ് സിദ്ധാന്തമാണ് അഫൈൻ ഗേജ് സിദ്ധാന്തം , ഇവിടെ ഗേജ് ഫീൽഡുകൾ സുഗമമായ മാനിഫോൾഡിനു മുകളിലുള്ള ടാൻജെന്റ് ബണ്ടിൽ അഫൈൻ കണക്ഷനുകളാണ് . ഉദാഹരണത്തിന്, ഇവ തുടർച്ചയായ മാധ്യമങ്ങളിലെ ഡിസ്ലോക്കേഷനുകളുടെ ഗേജ് സിദ്ധാന്തമാണ് , എപ്പോൾ മെട്രിക്-അഫൈൻ ഗുരുത്വാകർഷണ സിദ്ധാന്തത്തിന്റെ പൊതുവൽക്കരണം ഒരു ലോക മാനിഫോൾഡും പ്രത്യേകിച്ചും അഞ്ചാമത്തെ ശക്തിയുടെ ഗേജ് സിദ്ധാന്തവുമാണ്.
അഫൈൻ ഗ്രൂപ്പ്: ഗണിതശാസ്ത്രത്തിൽ ഒരു ഫീൽഡ് കെ മേൽ അഫ്ഫിനെ ഗ്രൂപ്പ് അല്ലെങ്കിൽ ഏതെങ്കിലും അഫ്ഫിനെ സ്ഥലം ജനറൽ അഫ്ഫിനെ ഗ്രൂപ്പ് തന്നെ സ്ഥലം നിന്ന് എല്ലാ ഇൻവേർട്ടിബിൾ അഫ്ഫിനെ രൂപാന്തരണങ്ങളും ഗ്രൂപ്പ് ആണ്.
ജ്യാമിതി ഉറപ്പിക്കുക: ഗണിതശാസ്ത്രത്തിൽ, അകലത്തിന്റെയും കോണിന്റെയും മെട്രിക് സങ്കൽപ്പങ്ങൾ ഉപയോഗിക്കാതിരിക്കുമ്പോൾ യൂക്ലിഡിയൻ ജ്യാമിതിയുടെ അവശേഷിക്കുന്നത് അഫൈൻ ജ്യാമിതിയാണ് .
കർവുകളുടെ ജ്യാമിതി ഉറപ്പിക്കുക: ഡിഫറൻഷ്യൽ ജ്യാമിതിയുടെ ഗണിതശാസ്ത്ര മേഖലയിൽ, ഒരു അഫൈൻ സ്പേസിലെ വളവുകളെക്കുറിച്ചുള്ള പഠനമാണ് കർവുകളുടെ അഫൈൻ ജ്യാമിതി , പ്രത്യേകിച്ചും പ്രത്യേക അഫൈൻ ഗ്രൂപ്പിന് കീഴിൽ മാറ്റമില്ലാത്ത അത്തരം വളവുകളുടെ സവിശേഷതകൾ
അഫൈൻ ഗ്രൂപ്പ്: ഗണിതശാസ്ത്രത്തിൽ ഒരു ഫീൽഡ് കെ മേൽ അഫ്ഫിനെ ഗ്രൂപ്പ് അല്ലെങ്കിൽ ഏതെങ്കിലും അഫ്ഫിനെ സ്ഥലം ജനറൽ അഫ്ഫിനെ ഗ്രൂപ്പ് തന്നെ സ്ഥലം നിന്ന് എല്ലാ ഇൻവേർട്ടിബിൾ അഫ്ഫിനെ രൂപാന്തരണങ്ങളും ഗ്രൂപ്പ് ആണ്.
ഗ്രൂപ്പ് സ്കീം: ഗണിതശാസ്ത്രത്തിൽ, ഒരു ഗ്രൂപ്പ് സ്കീം ഒരു കോമ്പോസിഷൻ നിയമം ഉൾക്കൊള്ളുന്ന ബീജഗണിത-ജ്യാമിതീയ വസ്‌തുവാണ്. ഗ്രൂപ്പ് സ്കീമുകൾ സ്വാഭാവികമായും സ്കീമുകളുടെ സമമിതികളായി ഉയർന്നുവരുന്നു, മാത്രമല്ല ബീജഗണിത ഗ്രൂപ്പുകളെ സാമാന്യവൽക്കരിക്കുകയും ചെയ്യുന്നു, എല്ലാ ബീജഗണിത ഗ്രൂപ്പുകൾക്കും ഗ്രൂപ്പ് സ്കീം ഘടനയുണ്ട്, എന്നാൽ ഗ്രൂപ്പ് സ്കീമുകൾ ഒരു ഫീൽഡിനെ ബന്ധിപ്പിക്കുകയോ സുഗമമാക്കുകയോ നിർവചിക്കുകയോ ചെയ്യുന്നില്ല. സമ്പന്നമായ അനന്തമായ ഘടനകളെക്കുറിച്ച് പഠിക്കാൻ ഈ അധിക സാമാന്യത ഒരാളെ അനുവദിക്കുന്നു, കൂടാതെ ഗണിത പ്രാധാന്യമുള്ള ചോദ്യങ്ങൾ മനസിലാക്കാനും ഉത്തരം നൽകാനും ഇത് സഹായിക്കും. എല്ലാ ഹോമോമോണിസങ്ങൾക്കും കേർണലുകളുള്ളതിനാൽ ഗ്രൂപ്പ് സ്കീമുകളുടെ വിഭാഗം ഗ്രൂപ്പ് ഇനങ്ങളേക്കാൾ മികച്ച രീതിയിൽ പെരുമാറുന്നു, കൂടാതെ നന്നായി പെരുമാറുന്ന രൂപഭേദം സിദ്ധാന്തവുമുണ്ട്. ബീജഗണിത ഗ്രൂപ്പുകളല്ലാത്ത ഗ്രൂപ്പ് സ്കീമുകൾ ഗണിത ജ്യാമിതിയിലും ബീജഗണിത ടോപ്പോളജിയിലും ഒരു പ്രധാന പങ്ക് വഹിക്കുന്നു, കാരണം അവ ഗാലോയിസ് പ്രാതിനിധ്യങ്ങളുടെയും മൊഡ്യൂളി പ്രശ്നങ്ങളുടെയും സന്ദർഭങ്ങളിൽ വരുന്നു. ഗ്രൂപ്പ് സ്കീമുകളുടെ സിദ്ധാന്തത്തിന്റെ പ്രാരംഭ വികാസം 1960 കളുടെ തുടക്കത്തിൽ അലക്സാണ്ടർ ഗ്രോതെൻഡിക്, മൈക്കൽ റെയ്ന ud ഡ്, മൈക്കൽ ഡെമാസുർ എന്നിവരാണ്.
ഹാഫ്-സ്പേസ് (ജ്യാമിതി): ജ്യാമിതിയിൽ, ഒരു വിമാനം ത്രിമാന യൂക്ലിഡിയൻ സ്ഥലത്തെ വിഭജിക്കുന്ന രണ്ട് ഭാഗങ്ങളിൽ ഒന്നിൽ പകുതി ഇടം. കൂടുതൽ സാധാരണമായി, ഒരു ഹൈപ്പർപ്ലെയിൻ ഒരു അഫൈൻ സ്പേസ് വിഭജിക്കുന്ന രണ്ട് ഭാഗങ്ങളിൽ ഒന്നാണ് പകുതി ഇടം. അതായത്, ഹൈപ്പർപ്ലെയിനിൽ സംഭവിക്കാത്ത പോയിന്റുകൾ രണ്ട് കോൺവെക്സ് സെറ്റുകളായി വിഭജിക്കപ്പെട്ടിട്ടുണ്ട്, അതായത് ഒരു സെറ്റിലെ ഒരു പോയിന്റിനെ മറ്റൊന്നിലെ ഒരു പോയിന്റുമായി ബന്ധിപ്പിക്കുന്ന ഏതൊരു ഉപമേഖലയും ഹൈപ്പർപ്ലെയിനെ വിഭജിക്കണം.
അഫെൻ ഹെക്ക് ആൾജിബ്ര: ഗണിതശാസ്ത്രത്തിൽ, ഒരു അഫൈൻ വെയിൽ ഗ്രൂപ്പുമായി ബന്ധപ്പെട്ട ബീജഗണിതമാണ് ഹെഫി ആൾജിബ്ര , ഇത് മക്ഡൊണാൾഡിന്റെ പോളിനോമിയലുകൾക്കുള്ള മക്ഡൊണാൾഡിന്റെ നിരന്തരമായ term ഹത്തെ തെളിയിക്കാൻ ഉപയോഗിക്കാം.
അഫൈൻ ഹൾ: , അഫ്ഫിനെ പള്ള അല്ലെങ്കിൽ യൂക്ലിഡിയൻ ആർ ഒരു സെറ്റ് എസ് എന്ന അഫ്ഫിനെ ചാൺ ഗണിതത്തിൽ n എസ് ഉൾക്കൊള്ളുന്ന ഏറ്റവും ചെറിയ അഫ്ഫിനെ സെറ്റ്, അല്ലെങ്കിൽ സമമായി, എസ് അടങ്ങുന്ന എല്ലാ അഫ്ഫിനെ സെറ്റ് യെ. ഇവിടെ, ഒരു വെക്റ്റർ ഉപമേഖലയുടെ വിവർത്തനമായി ഒരു അഫൈൻ സെറ്റ് നിർവചിക്കാം.